Zero-order rate law liner equation graph

General Chemistry

In a zero-order reaction, the rate of the reaction is independent of the concentration of the reactant. This can be seen in the differential rate law which shows how the rate of a reaction depends on the concentration of the reactant(s):

 

A → Products

Rate = k[A]0 = k

 

where k is the rate constant, and the exponent 0 is the reaction order, which in a general formula is given by n.

When n = 0, the [A]0 term equals 1, and therefore, the rate is equal to the rate constant of the reaction, and the concentration of reactant decreases linearly with time.

So, how do we understand that the rate does not depend on concentration? In other words, it means the amount of reactant that is actually available for reaction does not change with the overall quantity of reactant. Most zero-order reactions either require a catalyst or occur between gases in saturated containers.

For example, the reaction of H2 and Cl2 gases is catalyzed with light (photochemical reaction):

 

\[{{\rm{H}}_{\rm{2}}}\left( g \right){\rm{ }} + {\rm{ C}}{{\rm{l}}_{\rm{2}}}\left( g \right)\;\mathop  \to \limits^{hv} \,{\rm{2HCl}}\left( g \right)\]

 

The decomposition of nitrous oxide over the surface of a hot platinum catalyst is another zero-order reaction:

 

\[{\rm{2}}{{\rm{N}}_{\rm{2}}}{\rm{O}}\left( g \right){\rm{ }}\mathop  \to \limits^{Pt} {\rm{ 2}}{{\rm{N}}_{\rm{2}}}\left( g \right)\;\, + \;{{\rm{O}}_{\rm{2}}}\left( g \right)\]

 

As long as there is enough surface of the catalyst to capture all the reactant molecules, it does not matter how much of it there is – the reaction continues at the same rate.

 

Another example that is not a chemical reaction and generally follows the zero-order rules is sublimation. This is because only molecules at the surface of a substance can sublime, and their concentration does not change with the sublimation.

 

The Units of Rate Constant, k for a Zero-Order Reaction

Zero-order indicates that the rate does not depend on the concentration, and therefore, the rate is equal to the concentration.

rate = k[A]0

[A]0 = 1, therefore,

rate = k

The units for the rate are mol/L, so it is the same as the rate constant:

 

k = mol/L s or M/s or M x s-1

 

The following table summarizes the rate laws, half-lives, and k units for first-, second-, and zero-order reactions:

 

 

There is also a formula which you can use as a shortcut to determine the units of a rate constant:

k units = M1-n · t-1

where n is the reaction order

If we needed to determine the units of k for a zero order reaction, we would use 0 for the n:

k units = M1-0 · t-1 = M · t-1

 

The Integrated Rate Law of a Zero-Order Reaction 

Integrating the differential rate law, we obtain the integrated rate law for the first-order reactions. You can check this article for more details, but for now, we will write the final form of the integrated rate law for zero-order reactions.

For a simple hypothetical reaction where molecule A transforms into products, the (differential) rate law for a zero-order reaction can be written as:

 

A → Products

Rate = k[A]0 = k

 

Integrating the differential rate law, we obtain the integrated rate law for the zero-order reactions:

 

 

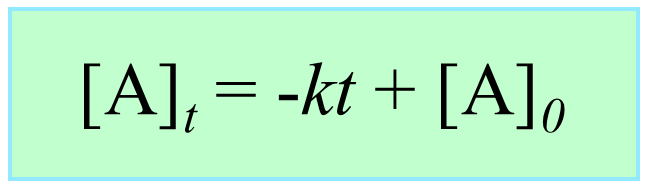
Note that the zero-order integrated rate law is also in the form of an equation for a straight line:

 

 

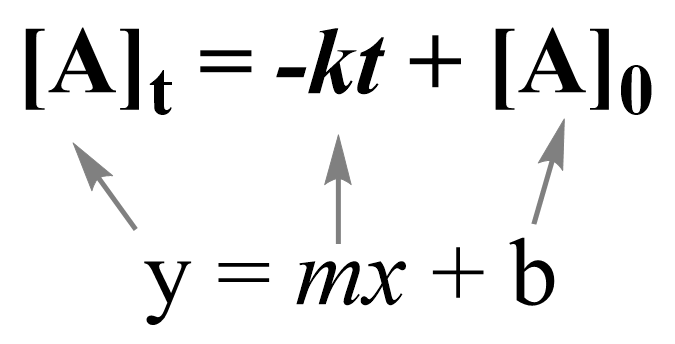
Therefore, a straight line with a slope of –k and an intercept of [A]0 is obtained in a graph of [A] versus time:

 

 

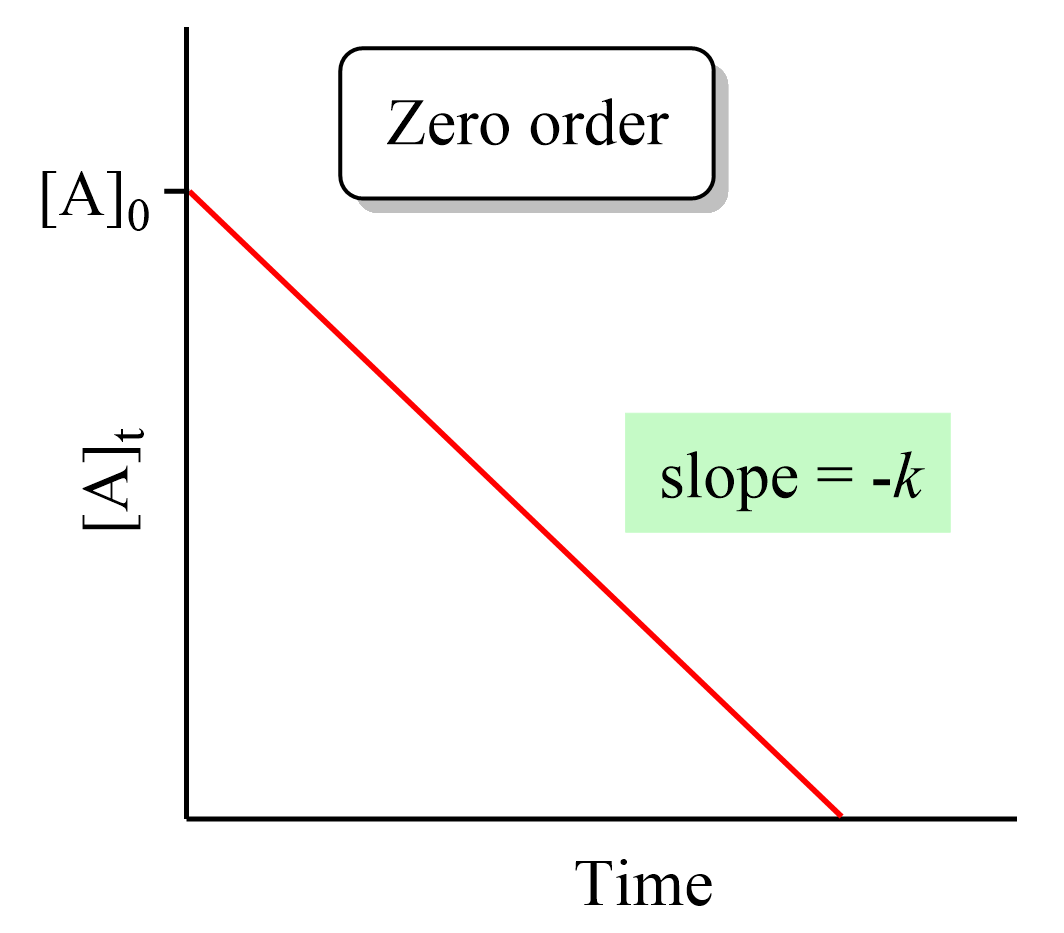
Remember, this was not the case for first- and second-order reactions where a straight line was obtained when the ln [A] and 1/[A] needed to be plotted vs time.

 

The Half-Life of Zero-Order Reactions

The integrated rate low for zero-order reactions A → Products is:

                                                                                    

\[{\left[ {\rm{A}} \right]_t}\; = \; – \;kt\, + \,{\left[ {\rm{A}} \right]_0}\]

 

Half-life is when the initial concentration [A]0 dropped by 50% which means:

                                                                                      

\[{\left[ {\rm{A}} \right]_{{t_{1/2}}}} = {\rm{ }}{\textstyle{1 \over 2}}{\left[ {\rm{A}} \right]_0}\]

 

So, replacing [A]t with 1/2[A]0, we get:

 

\[{\textstyle{1 \over 2}}{\left[ {\rm{A}} \right]_0}\; = \; – \;k{t_{1/2}}\, + \,{\left[ {\rm{A}} \right]_0}\]

 

W can now rearrange this equation to obtain the expression for the half-life of the zero-order reactions:

 

\[k{t_{1/2}}\; = \;{\textstyle{1 \over 2}}{\left[ {\rm{A}} \right]_0}\]

 

The equation indicates that the smaller the [A]0, the shorter the half-life or, in other words, the half-life of a zero-order reaction gets shorter as the concentration decreases.

To summarize, this is what we learned about the half-life of a reaction and its correlation with the concentration for a first-, second-, and zero-order reactions:

 

 

Notice that in all cases, the half-life depends on the rate constant which appears in the denominator. And this indicates that the faster the reaction, the shorter its half-life.

 

Check Also

 

Leave a Comment