When discussing the reaction order, we mentioned that the rate of a first- and second-order reaction depends on the concentration of the reactant.
For example, the rate for a simple first-order reaction can be shown as:
A → Products
Rate = k[A]
where k is the rate constant, and it is the proportionality linkage between the rate and the concentration.
It is, however, important to mention that the k is constant only at a given temperature. The dependence of the rate constant on the temperature is given by the Arrhenius equation:
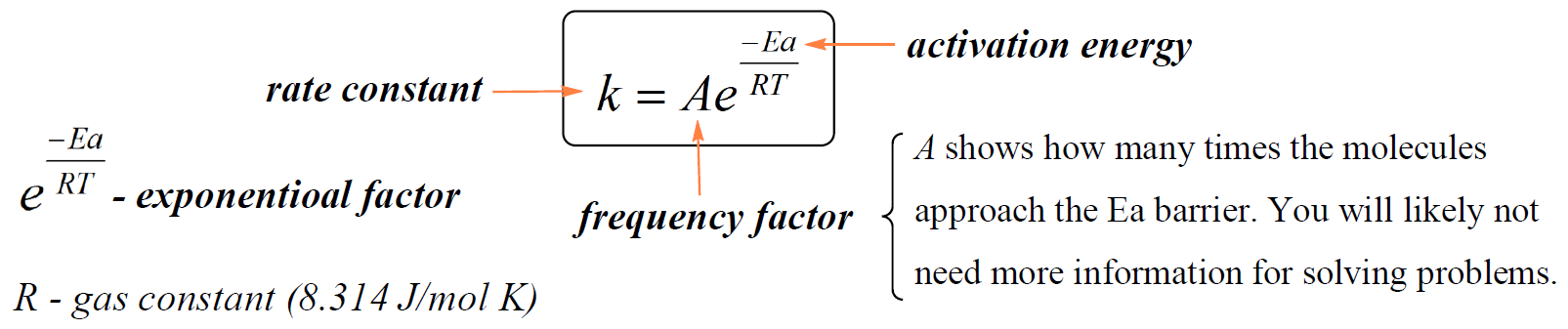
In this equation, A is a constant called the frequency factor (or the pre-exponential factor), Ea is the activation energy in kJ/mol, R is the gas constant (8.314 J/K · mol), T is the absolute temperature, and e is the base of the natural logarithm.
So, how do we interpret the Arrhenius equation? First, notice that it shows the correlation between the rate constant, activation energy, and temperature.
We can see that lowering the activation energy (Ea), increases the exponential factor, and therefore, k gets larger which indicates an increase of the reaction rate. This is expected because remember, activation energy is the energy barrier between the energy of the reactants and the transition state, and the lower it is, the faster the reaction because the molecules can easier overcome this barrier:
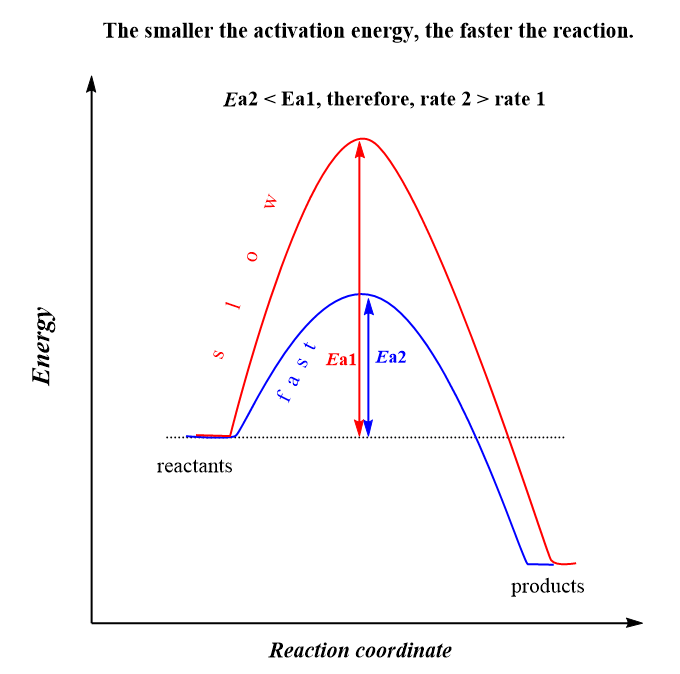
The second observation is that the rate constant, and therefore, the rate of the reaction, increases with temperature. Although T is in the denominator, the negative sign before the fraction, indicates that increasing the temperature, increases the exponential factor, and therefore, the k which ultimately increases the rate.
The reason for this is that increasing the temperature increases the kinetic energy of the molecules and therefore, the number of collisions between molecules with sufficient energy to surmount the activation energy barrier.
So, remember these correlations between the rate constant, activation energy, and temperature:
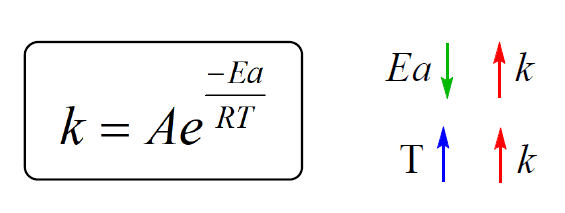
We have seen the effects of temperature and activation energy on the rate constant which are combined together in the exponential factor.
Now, how is A related to this?
The Frequency and Exponential Factors
The Frequency Factor A represents the frequency of collisions between molecules that lead to approaching the activation barrier per unit time.
Notice that not all the approaches result in passing the activation energy barrier and the fraction of the approaches that do, is given by the exponential factor. The exponential factor is a number between 0 and 1 that shows how many molecules that approach the activation barrier have enough energy to actually pass it.
For example, let’s say, in one second, there are 100 molecules of A and B approaching the activation barrier:
A + B → C + D
If the temperature is very high and the activation energy is so low that all these 100 molecules overcome it, the exponential factor then would be equal to 1 (e = 1). If, e = 0.5, then 50% of the molecules approaching the Ea barrier will react, etc.
In reality, the frequency factor is a lot larger, and the exponential factor is a lot smaller. For example, if the frequency factor is 108 s-1 (108 molecules approaching the activation energy barrier per one second), and the exponential factor is 10-6, the rate constant of the reaction will be 108 s-1 x 10-6 = 102 s-1.
An exponential factor of 10-6 means only 1 in 106 molecules has sufficient energy to actually pass the activation barrier.
Arrhenius Plots
The Arrhenius equation can be expressed in a more applicable form by taking the natural logarithm of both sides which gives a form of a linear equation:
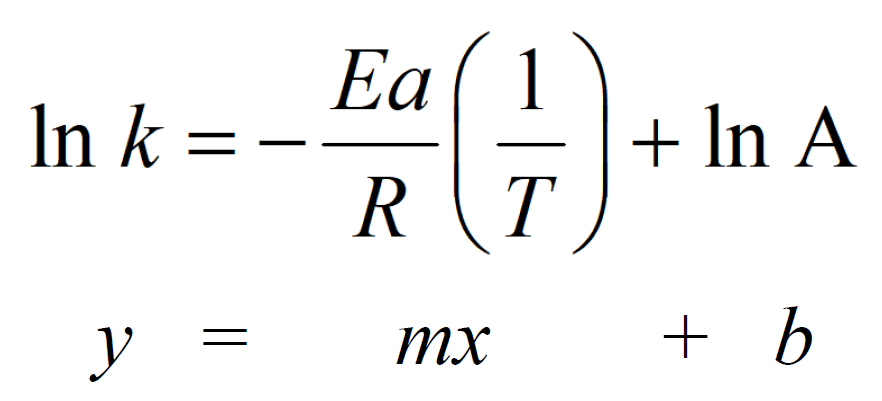
This means a plot of ln k versus 1/T gives a straight line with a slope (m) of –Ea/R and an intercept (b) of ln A. Therefore, we can determine the activation energy or the frequency factor by plotting the data for the rate constant values at different temperatures vs 1/T.
For example,
The table below shows the rate constants for a first-order rearrangement reaction at various temperatures.
a) Calculate the activation energy for the reaction by making a graph.
b) Calculate the activation energy for the reaction without making a graph.
|
k (s-1) |
T (K) |
|
0.022 |
1400 |
|
0.07 |
1460 |
|
0.21 |
1520 |
|
0.686 |
1580 |
|
1.578 |
1620 |
The first thing is to convert the data in the table to ln k vs 1/T because this is what gives a straight line when plotted:
|
ln k |
1/T (K-1) |
|
-3.81671 |
0.000714 |
|
-2.65926 |
0.000685 |
|
-1.56065 |
0.000658 |
|
-0.37688 |
0.000633 |
|
0.456158 |
0.000617 |
Once you have this, go ahead, and plot ln k on the Y and 1/T on the X-axis using excel or other suitable software:
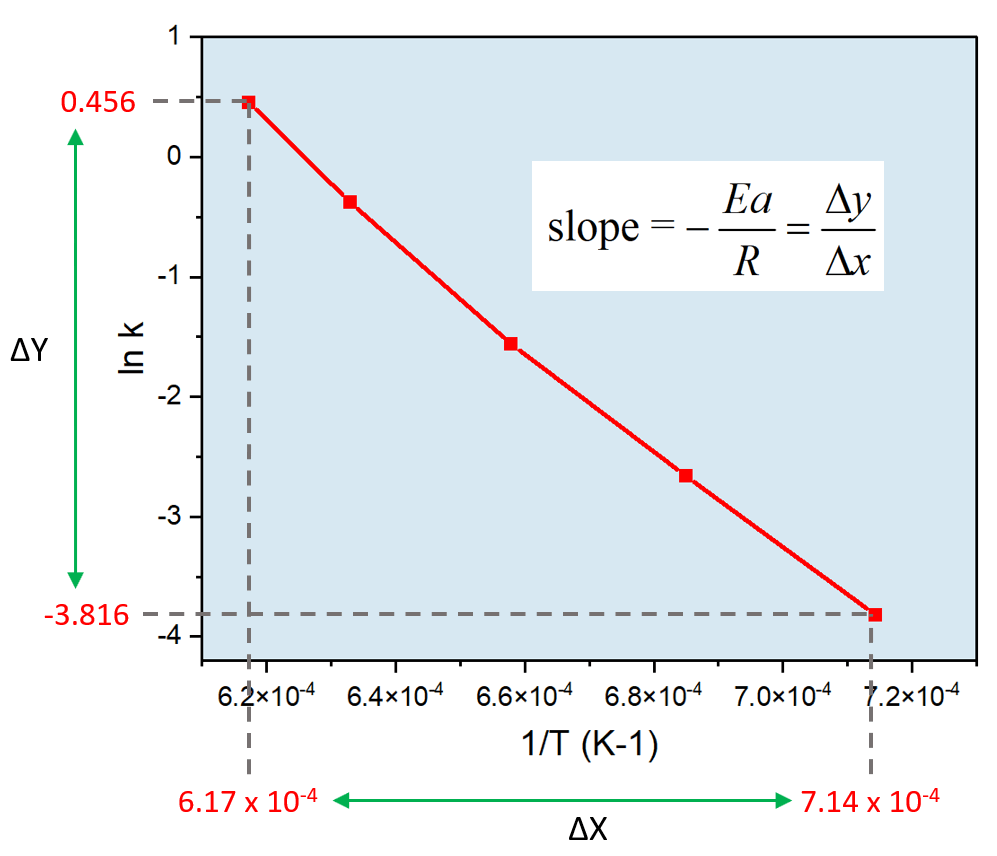
At this point, we can plug in the numbers to determine the activation energy:
\[ – \frac{{Ea}}{R} = \;\frac{{ – 3.816 – 0.456}}{{(7.14\; \times \,{{10}^{ – 4}} – 6.17\; \times \,{{10}^{ – 4}})\,{K^{ – 1}}}} = \; – 4.40\; \times \,{10^4}\,{\rm{K}}\]
\[{E_a}\; = \,{\rm{4}}{\rm{.40}}\;{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{\rm{4}}}{\rm{ }}\cancel{{\rm{K}}}{\rm{ \times }}\,\,{\rm{8}}{\rm{.314}}\,\frac{{\rm{J}}}{{\cancel{{\rm{K}}}\;{\rm{mol}}}}\]
\[{E_a} = \;3.65\,\; \times \,{10^5}\,{\rm{J/mol}}\;{\rm{ = }}\;{\rm{3}}{\rm{.65}}\, \times \,{10^2}\,{\rm{kJ/mol}}\]
Using Arrhenius Equation With No Graphs
The logarithmic form of the Arrhenius equation can also be used in a nongraphical way to determine if we know the rate constant of a reaction at two or more temperatures.
To do this, we write the Arrhenius equation for two temperatures and subtract them to get rid of the frequency factor A:
\[\ln \;{k_1}\; = \; – \frac{{Ea}}{R}\left( {\frac{1}{{{T_1}}}} \right)\; + \;\ln \;{\rm{A}}\]
\[\ln \;{k_2}\; = \; – \frac{{Ea}}{R}\left( {\frac{1}{{{T_2}}}} \right)\; + \;\ln \;{\rm{A}}\]
\[\ln \;{k_2}\; – \;\ln \;{k_1} = \;\left[ { – \frac{{Ea}}{R}\left( {\frac{1}{{{T_2}}}} \right)\; + \;\ln \;{\rm{A}}} \right]\;{\rm{ – }}\,\left[ { – \frac{{Ea}}{R}\left( {\frac{1}{{{T_1}}}} \right)\; + \;\ln \;{\rm{A}}} \right]\]
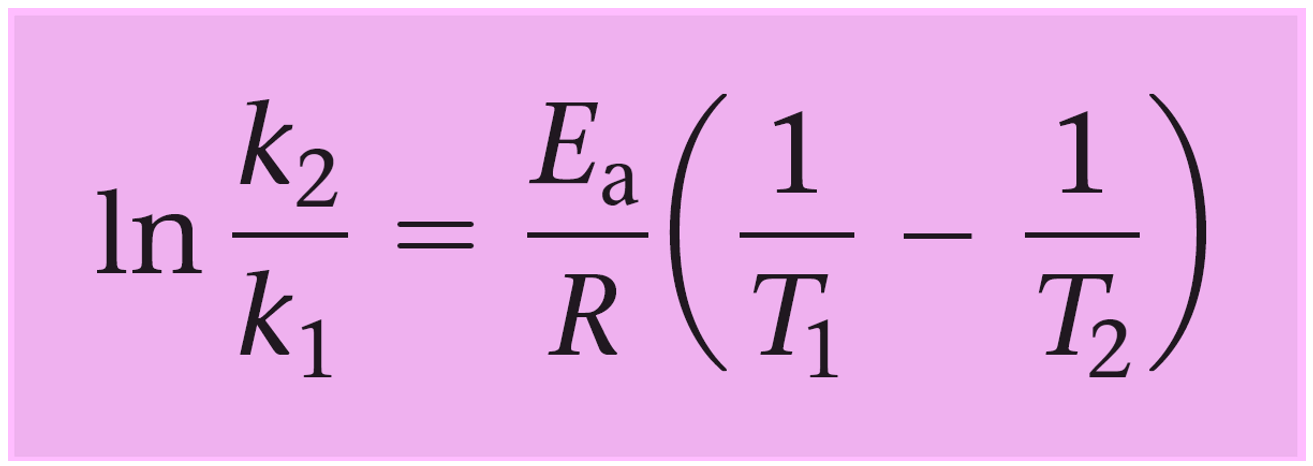
And now let’s see how this equation could have also been used to determine the activation energy in the previous example.
For this, we pick two values of the rate constant at temperature 1 and 2. So, let’s say T1 = 1400 K, k1 = 0.022 s-1, T2 = 1620 K, and k2 = 1.578 s-1.
Next, write the logarithmic form of the Arrhenius equation correlating the rate constants at two temperatures and plug in the numbers:
\[\ln \;\frac{{{k_2}}}{{{k_1}}}\; = \;\frac{{{E_a}}}{R}\left( {\frac{1}{{{T_1}}}\; – \;\frac{1}{{{T_2}}}} \right)\;\]
\[\ln \;\frac{{1.578\,{s^{ – 1}}\,}}{{0.022\;{s^{ – 1}}}}\; = \;\frac{{{E_a}}}{{{\rm{8}}{\rm{.314 J}}\;/\;{\rm{K mol}}}}\left( {\frac{1}{{1400\,{\rm{K}}}}\; – \;\frac{1}{{1620\;{\rm{K}}}}} \right)\;\]
\[4.2728\; = \;\frac{{{E_a}}}{{{\rm{8}}{\rm{.314 J}}\;/\;{\rm{mol}}}}\, \times \;9.70\, \times \,{10^{ – 5}}\]
\[4.2728\; \times \,{\rm{8}}{\rm{.314 J}}\;/{\rm{ mol}} = \;9.70\, \times \,{10^{ – 5}}\,{E_a}\]
Ea = 3.66 x 105 J/mol = 3.66 x 102 kJ/mol
The results are very close which confirms that both approaches, using the slope of the graph or calculating the Ea based on the values of the rate constant at two different temperatures can be used.
Let’s do another example by using the data for two temperatures and this time, determine the rate constant of the reaction.
And now let’s see how this can be used for determining the activation energy or the rate constant of a reaction at a specific temperature.
For example,
The rate constant of a first-order reaction is 4.65 x 10-2 s-1 at 298 K. What is the rate constant at 380 K if the activation energy for the reaction is 70.4 kJ/mol?
First, write what is given and what needs to be determined:
k1 = 4.65 x 10-2 s-1
T1 = 298 K
T2 = 380 K
k2 = ?
Next, write the logarithmic form of the Arrhenius equation correlating the rate constants at two temperatures and plug in the numbers:
\[\ln \;\frac{{{k_2}}}{{{k_1}}}\; = \;\frac{{{E_a}}}{R}\left( {\frac{1}{{{T_1}}}\; – \;\frac{1}{{{T_2}}}} \right)\;\]
\[\ln \;\frac{{{k_2}}}{{4.65{\rm{ }} \times {\rm{ }}{{10}^{ – 2}}{s^{ – 1}}}}\; = \;\frac{{70.4\; \times \;{{10}^3}\;{\rm{J/mol}}}}{{{\rm{8}}{\rm{.314 J}}\;/\;{\rm{K mol}}}}\left( {\frac{1}{{298\,{\rm{K}}}}\; – \;\frac{1}{{380\;{\rm{K}}}}} \right)\;\]
\[\ln \;\frac{{{k_2}}}{{4.65{\rm{ }} \times {\rm{ }}{{10}^{ – 2}}{s^{ – 1}}}}\; = \;6.13164\]
\[\frac{{{k_2}}}{{4.65{\rm{ }} \times {\rm{ }}{{10}^{ – 2}}{s^{ – 1}}}}\; = \;{e^{6.13164}}\]
\[\frac{{{k_2}}}{{4.65{\rm{ }} \times {\rm{ }}{{10}^{ – 2}}{s^{ – 1}}}}\; = \;{\rm{460}}{\rm{.19}}\]
K2 = 4.65 x 10-2 s-1 x 460.19 = 21.39 s-1
The answer is reasonable because the rate constant is expected to be larger at a higher temperature.
Here is a 77-question, Multiple-Choice Quiz on Chemical Kinetics:
Check Also
- Reaction Rate
- Rate Law and Reaction Order
- How to Determine the Reaction Order
- Integrated Rate Law
- The Half-Life of a Reaction
- Determining the Reaction Order Using Graphs
- Units of Rate Constant k
- How Are Integrated Rate Laws Obtained
- Activation Energy
- Chemical Kinetics Practice Problems

