We mentioned in the previous post that the order of a reaction can be determined only by experiment. Most often, this experiment consists of measuring the initial rate of the reaction by changing the concentration of the reactant and monitoring how it affects the rate.
For example, the rate law for a hypothetical reaction where molecule A transforms into products can be written as:
A → Products
Rate = k[A]n
where k is the rate constant and n is the reaction order.
Our objective is to determine the reaction order by calculating the n from a set of experiments. Keep in mind that:
- If n = 0, the reaction is zero-order, and the rate is independent of the concentration of A.
- If n = 1, the reaction is first-order, and the rate is directly proportional to the concentration of A.
- If n = 2, the reaction is second-order, and the rate is proportional to the square of the concentration of A.
Now, suppose we run three experiments, and the following data is obtained for the concentration-rate correlation:

In every experiment, the concentration of A is doubled, and what we see is that the rate of the reaction doubles as well. Therefore, the initial rate is directly proportional to the initial concentration, and thus, we have a first-order reaction:
Rate = k[A]1
If it was a zero-order reaction, the following data for the concentration-rate relationship would have been obtained:
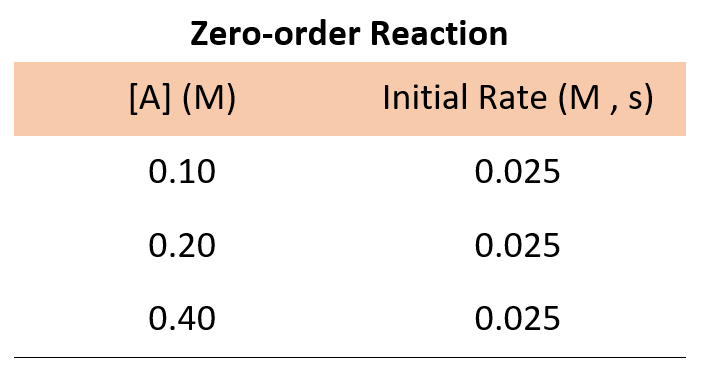
The data for a zero-order reaction indicates that the rate does not depend on the concentration of reactants.
For a second-order reaction, doubling the concertation quadrupoles the reaction rate, and therefore, we would expect the following data:
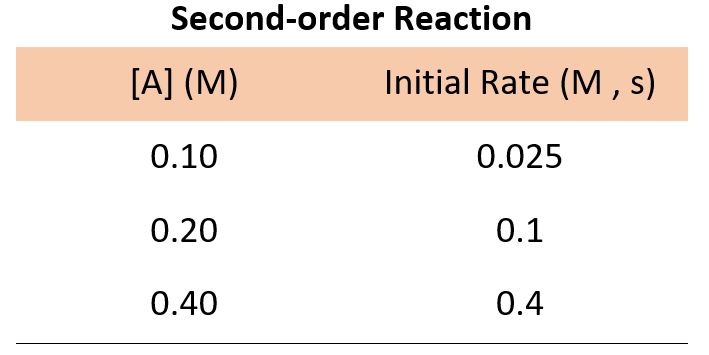
If the numbers are not obvious for determining how the rate changes with concentration, you can pick the data from any set of two experiments, write the rate law, and divide them to see how the rate changes.
For example, going back to the data for a first-order reaction, we can divide the rate of experiments 1 and 2:

\[\frac{{Rate\;2}}{{Rate\;1}}\;{\rm{ = }}\;\frac{{k{{[{{\rm{A}}_2}]}^{\rm{n}}}}}{{k{{[{{\rm{A}}_1}]}^{\rm{n}}}}}\;{\rm{ = }}\;\frac{{{\rm{0}}{\rm{.050}}\;M{\rm{/s}}}}{{{\rm{0}}{\rm{.025}}\,M{\rm{/s}}}}\]
\[\frac{{Rate\;2}}{{Rate\;1}}\;{\rm{ = }}\;\frac{{\cancel{k}{{{\rm{(0}}{\rm{.20}}\,\cancel{M}{\rm{)}}}^{\rm{n}}}}}{{\cancel{k}{{{\rm{(0}}{\rm{.10}}\,\cancel{M}{\rm{)}}}^{\rm{n}}}}}\;{\rm{ = }}\;\frac{{{\rm{0}}{\rm{.050}}\;\cancel{{M{\rm{/s}}}}}}{{{\rm{0}}{\rm{.025}}\,\cancel{{M{\rm{/s}}}}}}\]
\[\frac{{{{{\rm{(0}}{\rm{.20}}\,{\rm{)}}}^{\rm{n}}}}}{{{{{\rm{(0}}{\rm{.10}}\,{\rm{)}}}^{\rm{n}}}}}\;{\rm{ = }}\;2\]
2n = 2, therefore,
n = 1
Determining the Value of Rate Constant
To determine the value of the rate constant, write the rate law expression:
Rate = k[A]
Now, you can pick data from any experiment and plug the numbers into a rate law experiment. Let’s use the data from experiment 1.
Rate1 = k[A1]
\[k\, = \,\frac{{{\rm{rat}}{{\rm{e}}_{\rm{1}}}}}{{\left[ {{{\rm{A}}_{\rm{1}}}} \right]}}\; = \;\frac{{0.025\,M/s}}{{0.10\,M}}\; = \;0.25\,{s^{ – 1}}\]
Let’s now do another example with a real reaction between carbon dioxide and hydrogen and determine the reaction order with respect to each reactant, the overall order, and the value of the rate constant.
Example:
Carbon dioxide, CO2, reacts with hydrogen to give methanol (CH3OH), and water.
CO2(g) + 3H2(g) ⇆ CH3OH(g) + H2O(g)
In a series of experiments, the following initial rates of disappearance of CO2 were obtained:
| Exp. | [CO2] | [H2] | Initial rate, M/s |
| 1 | 0.640 | 0.220 | 2.7 x 10-3 |
| 2 | 1.28 | 0.220 | 1.08 x 10-2 |
| 3 | 0.640 | 0.440 | 5.4 x 10-3 |
Determine the rate law and calculate the value of the rate constant for this reaction.
Solution:
To determine the overall reaction order, we need to determine it with respect to both reactants. Let’s first determine the order in CO2. Find two experiments where the concentration of H2 is kept constant while the concentration of CO2 is changed. In experiments 1 and 2, the concentration of CO2 is doubled from 0.640 M to 1.28 M while the concentration of H2 is kept at 0.220 M. We see from the table, that doubling the concentration of CO2 quadruples the rate of the reaction (1.08 x 10-2 ÷ 2.7 x 10-3 = 4). Therefore, the reaction is second-order in CO2.
Now, let’s find two experiments where the concentration of CO2 is kept constant while that of H2 is changed. In experiments 1 and 3, the concentration of CO2 is kept at 0640 M while the concentration of H2 is doubled from 0.220 M to 0.440 M. We see from the table, that doubling the concentration of H2 had doubled the reaction rate (5.4 x 10-3 ÷ 2.7 x 10-3 = 2 ). Therefore, the reaction is first-order in H2.
The rate law, therefore, is:
Rate = k[CO2]2[H2]
And the overall order of the reaction is 2+1 = 3 – it is a third-order reaction.
To calculate the value of the rate constant, use the numbers from any experiment for the following equation:
\[k\; = \;\frac{{{\rm{rate}}}}{{{{\left[ {{\rm{C}}{{\rm{O}}_{\rm{2}}}} \right]}^2}\left[ {{{\rm{H}}_{\rm{2}}}} \right]}}\]
\[k\; = \;\frac{{{\rm{2}}{\rm{.7 \times 1}}{{\rm{0}}^{{\rm{ – 3}}}}\;\cancel{{\rm{M}}}{\rm{/s}}}}{{{{\left( {{\rm{0}}{\rm{.640}}\;{\rm{M}}} \right)}^{\rm{2}}}\left( {{\rm{0}}{\rm{.220}}\;\cancel{{\rm{M}}}} \right)}}\;{\rm{ = }}\;{\rm{3}}{\rm{.00 \times 1}}{{\rm{0}}^{{\rm{ – 2}}}}\;{{\rm{M}}^{{\rm{ – 2}}}}{{\rm{s}}^{{\rm{ – 1}}}}\;\]
Here is a 77-question, Multiple-Choice Quiz on Chemical Kinetics:
Check Also
Practice
Iron(II) ion is oxidized by hydrogen peroxide in an acidic solution.
2Fe2+ (aq) + H2O2(aq) + 2H+(aq) → 2Fe3+(aq) + 2H2O(l)
The rate law for the reaction is determined to be rate = k[H2O2 ][Fe2+]. The rate constant, at certain temperature, is 2.56 x 1024/M · s. Calculate the rate of the reaction at this temperature if [H2O2 ] = 0.48 M and [H2O2] = 0.070 M.
For the kinetics of the reaction
2NO(g) + Cl2(g) → 2NOCl(g)
The following data were obtained:
| Exp. | [NOCl] | [Cl2] | Initial rate, M/s |
| 1 | 0.25 | 0.35 | 0.68 |
| 2 | 0.25 | 0.70 | 1.36 |
| 3 | 0.50 | 0.70 | 2.72 |
a) What is reaction order in Cl2 and NO?
b) What is the rate law?
c) What is the value of the rate constant?
The date for the initial rate of the following reaction is listed in the table below:
A + B → C + D
| Exp. | [A] | [B] | Initial rate, M/s |
| 1 | 0.370 | 0.248 | 2.45 x 10-3 |
| 2 | 0.370 | 0.496 | 9.8 x 10-3 |
| 3 | 0.740 | 0.248 | 4.9 x 10-3 |
| 4 | 0.740 | 0.496 | 1.96 x 10-2 |
(a) What is the order of reaction with respect to A and to B?
(b) What is the overall reaction order?
(c) What is the value of the rate constant, k?
Consider the reaction
A(g) + B(g) ⇌ C(g)
The following data were obtained at a certain temperature:
| Exp. | [A] | [B] | Initial rate, M/s |
| 1 | 2.40 | 3.60 | 4.8 x 10-2 |
| 2 | 2.40 | 7.20 | 4.8 x 10-2 |
| 3 | 4.80 | 3.60 | 9.6 x 10-2 |
Using the data, determine the order of the reaction and calculate the rate constant:

