Average Rate of a Reaction
Chemical kinetics studies the rates of chemical reactions which is a measure of how fast they occur.
Similarly, the rate of a chemical reaction is measured as a change in the amounts of reactants or products (usually in molarity units) divided by the time the change occurred.
For example, let’s say in a reaction between hydrogen and chlorine gases, the concentration of H2 depressed from 2 mol/l to 1.4 mol/l in 180 seconds.
H2(g) + Cl2(g) → 2HCl(g)
The rate of the reaction can be written as:
\[{\rm{rate}}\;{\rm{ = }}\;{\rm{ – }}\;\frac{{{\rm{\Delta }}\left[ {{{\rm{H}}_{\rm{2}}}} \right]}}{{{\rm{\Delta t}}}}\;{\rm{ = }}\; – \frac{{\left( {{\rm{1}}{\rm{.4}}\;{\rm{ – }}\;{\rm{2}}} \right)\,{\rm{mol/L}}}}{{{\rm{50}}\;{\rm{s}}}}\, = \,0.012\,M/s\]
Note that we add a negative sign because the concentration of hydrogen decreases and without adding it, the rate would also be negative. This applies for the rate of disappearance of any reactant and therefore, a negative sign is always added.
Now, let’s look at how the concentration and the rate of formation of the product HCl can be represented. It is important to pay attention to the stoichiometric ratio of the reactants and components in the chemical equation.
For example, in this reaction, the molar ratio of H2 and HCl is 1:2 which means there is always going to be two times more HCl forming than H2 reacting.
If 0.6 mol/L H2 reacted in 50 s, there is going to be 1.2 mol/l HCl formed and if we divide this number by 50 s, the rate would be 0.024 M/s. We got two different numbers and the question is which one is the correct rate of the reaction?
So here is the thing, when we divide the change of concentration of any reactant or product, we are getting its depletion or formation rate which can be different if their coefficients are different. Therefore, to keep the reaction rate applicable and identical to all the reactants, and components, we divide their rates of depletion and formation by their coefficients in the chemical reaction.
The general formula for the reaction rate, based on the coefficients, can be written as:
aA + bB → cC + dD
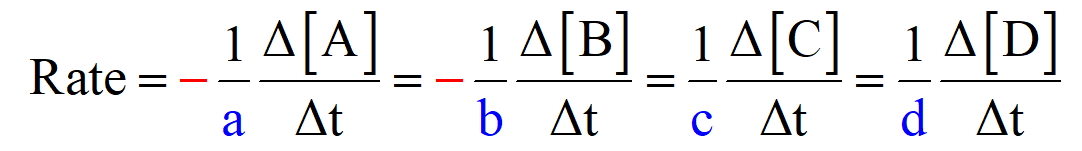
So, for our reaction, the reaction rate would be:
H2(g) + Cl2(g) → 2HCl(g)
\[rate\; = \;{\rm{ – }}\;\frac{{{\rm{\Delta }}\left[ {{{\rm{H}}_{\rm{2}}}} \right]}}{{{\rm{\Delta t}}}}\;{\rm{ = – }}\;\frac{{{\rm{\Delta }}\left[ {{\rm{C}}{{\rm{l}}_{\rm{2}}}} \right]}}{{{\rm{\Delta t}}}}\;{\rm{ = }}\frac{{\rm{1}}}{{\rm{2}}}\frac{{{\rm{\Delta }}\left[ {{\rm{HCl}}} \right]}}{{{\rm{\Delta t}}}}\;\]
And if we plug the numbers, the rate of the reaction is now identical regardless of which component ewe use to calculate it:
\[{\rm{rate}}\;{\rm{ = }}\;{\rm{ – }}\;\frac{{{\rm{\Delta }}\left[ {{{\rm{H}}_{\rm{2}}}} \right]}}{{{\rm{\Delta t}}}}\;{\rm{ = }}\; – \frac{{\left( {{\rm{1}}{\rm{.4}}\;{\rm{ – }}\;{\rm{2}}} \right)\,{\rm{mol/L}}}}{{{\rm{50}}\;{\rm{s}}}}\, = \,0.012\,M/s\]
\[rate\; = \;\frac{{\rm{1}}}{{\rm{2}}}\frac{{{\rm{\Delta }}\left[ {{\rm{HCl}}} \right]}}{{{\rm{\Delta t}}}}\; = \;\frac{{\rm{1}}}{{\rm{2}}}\frac{{{\rm{1}}{\rm{.2}}\;{\rm{mol/L}}}}{{{\rm{50}}\,{\rm{s}}}}\, = \;0.012\,M/s\]
Instantaneous Rate
The rate of the reaction is not constant, and it may be changing with the concentration of the reactants. Just like when we divide the distance we drove by the time we spent on it, we get the average speed which was not necessarily constant all the time. Therefore, what we discussed so far is the average rate of the reaction and the equation using the coefficients is to calculate the average rate of the reaction.
To describe the rate of the reaction at specific moment, we use what is called the instantaneous rate of a reaction. The instantaneous rate of a reaction is the rate at a particular instant during the reaction. It can be determined from the slope of the curve at a particular point in time.
For example, let’s say we are studying the rate of the following hypothetical reaction:
A + B → C + D
To determine the instantaneous rate at, for example, 80 s, we draw the tangent for that pointing going connecting any distinguishable time points and calculate the slope of the tangent:
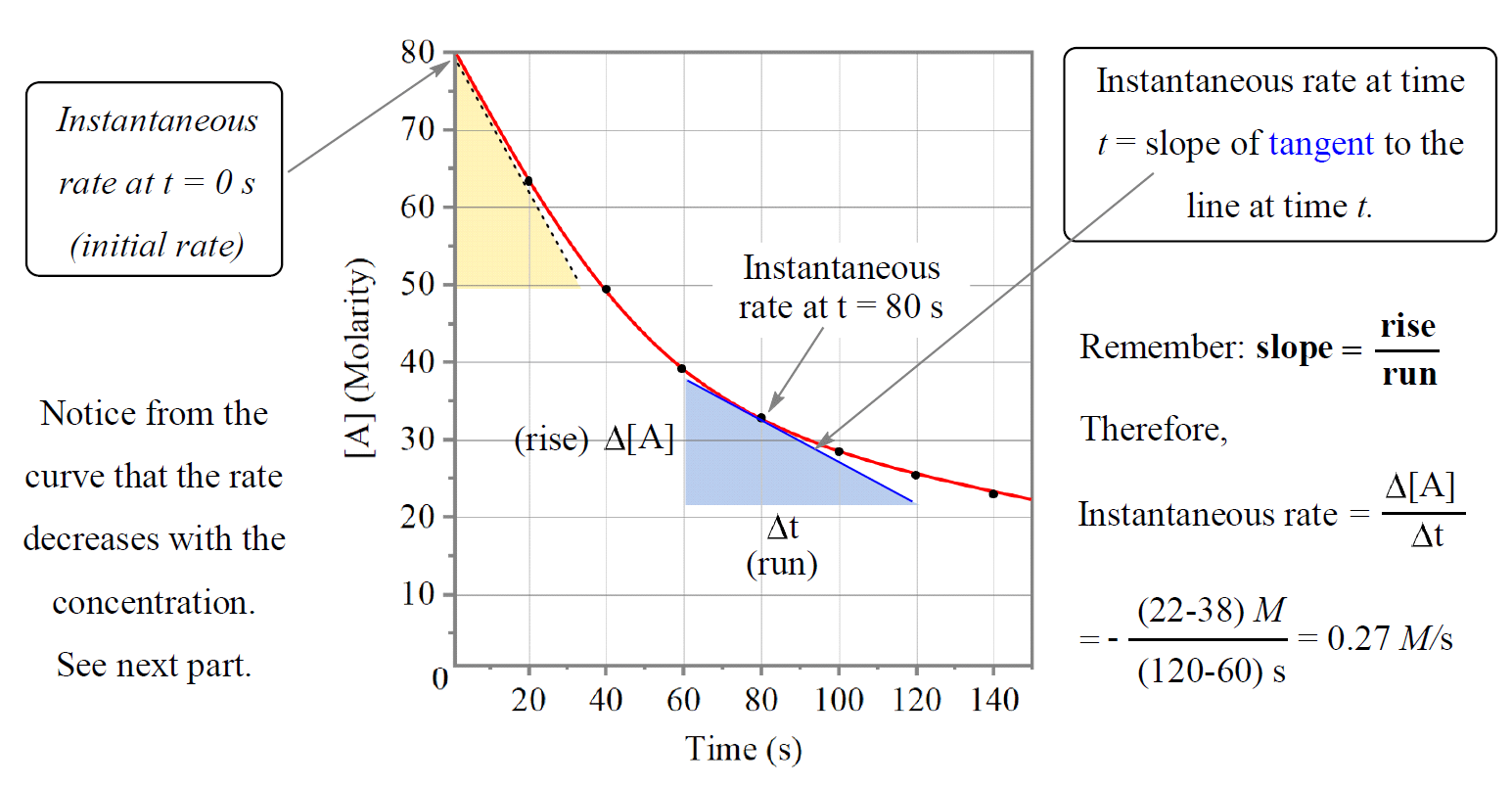
In this case, we draw the tangent from 60 to 120 s, so to determine the instantaneous rate, we locate the points showing the concentration change of reactant “A” and it looks to be 38 mol/L and 22 mol/L.
The slope is then calculated by the ratio Δy/ Δx:
\[{\rm{slope}}\;{\rm{ = }}\;\frac{{{\rm{\Delta y}}}}{{{\rm{\Delta x}}}}\;{\rm{ = }}\;\frac{{{\rm{\Delta [A]}}}}{{{\rm{\Delta T}}}}\;{\rm{ = }}\; – \frac{{{\rm{(22 – 38)}}\,M}}{{\left( {{\rm{120}}\,{\rm{ – }}\,{\rm{60}}} \right)\,s}}{\rm{ = }}\;{\rm{0}}{\rm{.27}}\,M/s\]
*Just noticed that I forget to change the concretions to smaller numbers as molarity couldn’t be 80 M. This does not change anything we discussed conceptually and the only difference is that smaller concentrations would give smaller rates.
The instantaneous rate at the beginning of the reaction (t = 0) is called the initial rate of the reaction.
The tangent line falls from [A]= 80 M to 50 M in the time change from 0 s to ~37 s. Therefore, the initial rate would be:
\[{\rm{slope}}\;{\rm{ = }}\;\frac{{{\rm{\Delta y}}}}{{{\rm{\Delta x}}}}\;{\rm{ = }}\;\frac{{{\rm{\Delta [A]}}}}{{{\rm{\Delta T}}}}\;{\rm{ = }}\; – \frac{{{\rm{(50 – 80)}}\,M}}{{\left( {{\rm{37}}\,{\rm{ – }}\,{\rm{0}}} \right)\,s}}{\rm{ = }}\;{\rm{0}}{\rm{.81}}\,M/s\]
Comparing the initial rate with the rate at 80s, we can see that it goes down as the concentration decreases. This is a general trend for most reactions; the rate is faster in the beginning when there is more reactants present and it slows down as the concentrations decrease. For some reactions though, the rate does not change with concentration.
Now, how exactly the rate depends on the concentration is described by rate laws which we will discuss in the next article.
Here is a 77-question, Multiple-Choice Quiz on Chemical Kinetics:
Check Also

