The half-life (t1/2) of a reaction is the time required for the concentration of a reactant to drop to one-half of its initial value.
The half-life depends on the order of the reaction, and it is obtained from the corresponding integrated rate law.
First-Order Reaction Half-Life
The half-life of the first-order reactions is obtained from the integrated rate law by replacing [A]t with 1/2[A]0:
\[\ln \;\frac{{{{[A]}_t}}}{{ {{[A]}_0}}}\; = \; – kt\]
Half-life is when the initial concentration [A]0 dropped by 50% which means
\[\ln \;\frac{{{\textstyle{1 \over 2}}\cancel{{{{[A]}_0}}}}}{{ \cancel{{{{[A]}_0}}}}}\; = \;\ln \frac{1}{2}\, = \; – k{t_{1/2}}\]
Therefore,
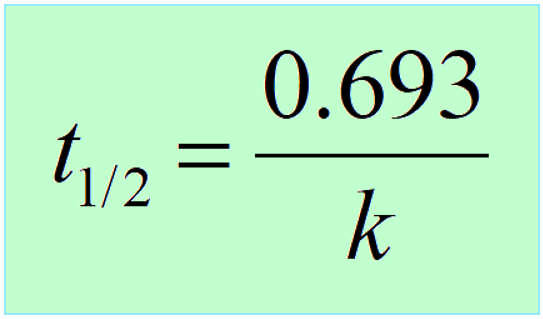
Interestingly, the half-life of first-order reactions does not depend on the initial concentration of the reactant.
So, if we start a reaction with a 10 M reactant, it will take the same time for it to decrease to 5 M as it does for dropping from 5 M to 2.5 M, and consequently from 2.5 M to 1.25 M.
The reason for this is that in a first-order reaction, the reactant molecules do not collide with proper energy and orientation which is the requirement for a reaction between two molecules to occur. Each molecule transforms into the product(s) by itself and has no effect on the reaction rate. Perhaps, the example of a cable car is a good analogy: if it takes 10 min to reach the destination, the number of people (reactant concentration) in the cabin does not matter.
Second-Order Reaction Half-Life
Like the first-order reactions, the half-life of second-order reactions is derived from the integrated rate law:
\[\frac{1}{{ {{[A]}_t}}}\; = \;kt\; + \;\frac{1}{{ {{[A]}_0}}}\;\;\]
Replacing [A]t with 1/2[A]0, we get:
\[\frac{1}{{ {\textstyle{1 \over 2}}{{[A]}_0}}}\; = \;k{t_{1/2}}\; + \;\frac{1}{{ {{[A]}_0}}}\;\;\]
And now we can rearrange the equation for the half-life:
\[k{t_{1/2}}\, = \,\frac{2}{{ {{[A]}_0}}}\; – \;\frac{1}{{ {{[A]}_0}}}\;\;\]
\[{t_{1/2}}\, = \,\frac{1}{{ k{{[A]}_0}}}\;\;\]
This indicates that the half-life of a second-order reaction depends on the initial concentration of the reactant, and the lower the initial concentration, the longer the half-life.
To understand this correlation, we need to remember that a second-order reaction occurs when two reactant molecules collide with sufficient energy and proper orientation. Therefore, the higher the concentration, the higher the probability of these collisions, the faster the rate, and therefore, the shorter the half-life.
The opposite is also true, the lower the initial concentration, the lower the probability of the collisions and thus, the longer the half-life.
Zero-Order Reaction Half-Life
The integrated rate low for zero-order reactions A → Products is:
\[{\left[ {\rm{A}} \right]_t}\; = \; – \;kt\, + \,{\left[ {\rm{A}} \right]_0}\]
Half-life is when the initial concentration [A]0 dropped by 50% which means:
\[{\left[ {\rm{A}} \right]_{{t_{1/2}}}} = {\rm{ }}{\textstyle{1 \over 2}}{\left[ {\rm{A}} \right]_0}\]
So, replacing [A]t with 1/2[A]0, we get:
\[{\textstyle{1 \over 2}}{\left[ {\rm{A}} \right]_0}\; = \; – \;k{t_{1/2}}\, + \,{\left[ {\rm{A}} \right]_0}\]
We can now rearrange this equation to obtain the expression for the half-life of the zero-order reactions:
\[k{t_{1/2}}\; = \;{\textstyle{1 \over 2}}{\left[ {\rm{A}} \right]_0}\]
The equation indicates that the smaller the [A]0, the shorter the half-life or, in other words, the half-life of a zero-order reaction gets shorter as the concentration decreases.
And the reason for this is that most zero-order reactions either require a catalyst or occur between gases in saturated containers. So, as long as there is enough surface of the catalyst to capture all the reactant molecules, it does not matter how much of it there is – the reaction continues at the same rate. This, in turn, means that the half-life keeps getting shorter as the reaction continues and the concentration decreases.
To summarize, this is what we learned about the half-life of a reaction and its correlation with the concentration for a first-, second-, and zero-order reactions:
Notice that in all cases, the half-life depends on the rate constant which appears in the denominator. And this indicates that the faster the reaction, the shorter its half-life.
Here is a 77-question, Multiple-Choice Quiz on Chemical Kinetics:
Check Also
Practice
The following decomposition of phosphorus pentachloride (PCl5) was found to be a first-order reaction:
PCl5(g) → PCl3(g) + 6Cl2(g)
The half-life of the reaction is 48.0 s at a certain temperature. Calculate (a) the first-order rate constant for the reaction and (b) the time required for 75 percent of the phosphorus pentachloride to decompose.


