In a second-order reaction, the rate of the reaction is proportional to the square of the concentration of the reactant. This can be seen in the differential rate law which shows how the rate of a reaction depends on the concentration of the reactant(s):
A → Products
Rate = k[A]2
where k is the rate constant, and the exponent 2 is the reaction order, which, in a general formula is given by n.
When n = 2, the rate squares in response to the increasing the reactant concentration. For example, doubling the concertation quadrupoles the reaction rate, while increasing the concentration three times speeds up the rate nine times.
Let’s say the concentration of A changes from 3 M to 6 M. The rate for these two concentrations would be:
Rate1 = k[3]2 = 9k
Rate2 = k[6]2 = 36k
The rate increases four times when we double the concertation of A. So, remember, in second-order reactions, the rate is proportional to the square of the concentration of the reactant which is why it is squared in the integrated rate law.
The Units of Rate Constant, k for a Second-Order Reaction
Most often, the reaction rate shows how the concentration changes with time, and therefore, the units of the rate are mol/L. If we rearrange the equation, we can obtain an expression for the rate constant as follows:
rate = k[A]2
\[k\; = \;\frac{{{\rm{rate}}}}{{{{\left[ {\rm{A}} \right]}^2}}}\]
And now, add the units for the rate and concentration:
\[k\; = \;\frac{{{\rm{mol}}}}{{{\rm{L}}\; \times \;{\rm{s}}}}\; \div \;{\left( {\frac{{{\rm{mol}}}}{{{\rm{L}}\;}}} \right)^2}\; = \;\frac{{\cancel{{{\rm{mol}}}}}}{{\cancel{{\rm{L}}}\;{\rm{ \times }}\;{\rm{s}}}}\;{\rm{ \times }}\;\frac{{{{\rm{L}}^{\cancel{{\rm{2}}}}}}}{{{\rm{mol}}\cancel{{^{\rm{2}}}}}}\;\;{\rm{ = }}\;\frac{{\rm{L}}}{{{\rm{mol}}\; \times \;{\rm{s}}}}\]
Alternatively, this can be written as M-1 · s-1:
The following table summarizes the rate laws, half-lives, and k units for first-, second-, and zero-order reactions:

There is also a formula that you can use as a shortcut to determine the units of a rate constant:
k units = M1-n · t-1
where n is the reaction order
If we needed to determine the units of k for a second-order reaction, we would use 1 for the n:
k units = M1-2 · t-1 = M-1 · t-1
So, if the time is given in seconds, k would be M-1 · s-1, for minutes, M-1 · min-1, and so forth.
Another example, let’s say we want to determine the units of the rate constant for third-order reactions.
n = 3, and therefore,
k units = M1-3 · t-1 = M-2 · t-1
If the time is seconds, then the units will be:
k units = M-2 · s-1
The Integrated Rate Law of a Second-Order Reaction
Integrating the differential rate law, we obtain the integrated rate law for the first-order reactions. You can check this article for more details, but for now, we will write the final form of the integrated rate law for second-order reactions:
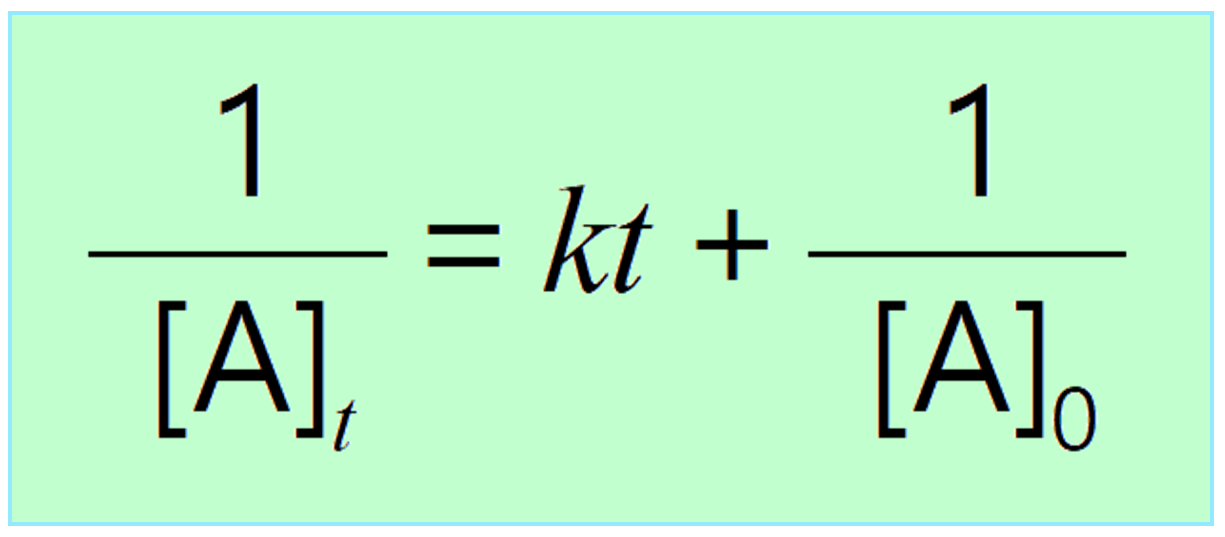
Just like the zero- and first-order reactions, the integrated rate law of second-order reaction is also in the form of a straight line where the 1/[A]t versus time yields a straight line with a slope of k and a y-intercept of 1/[A]0.
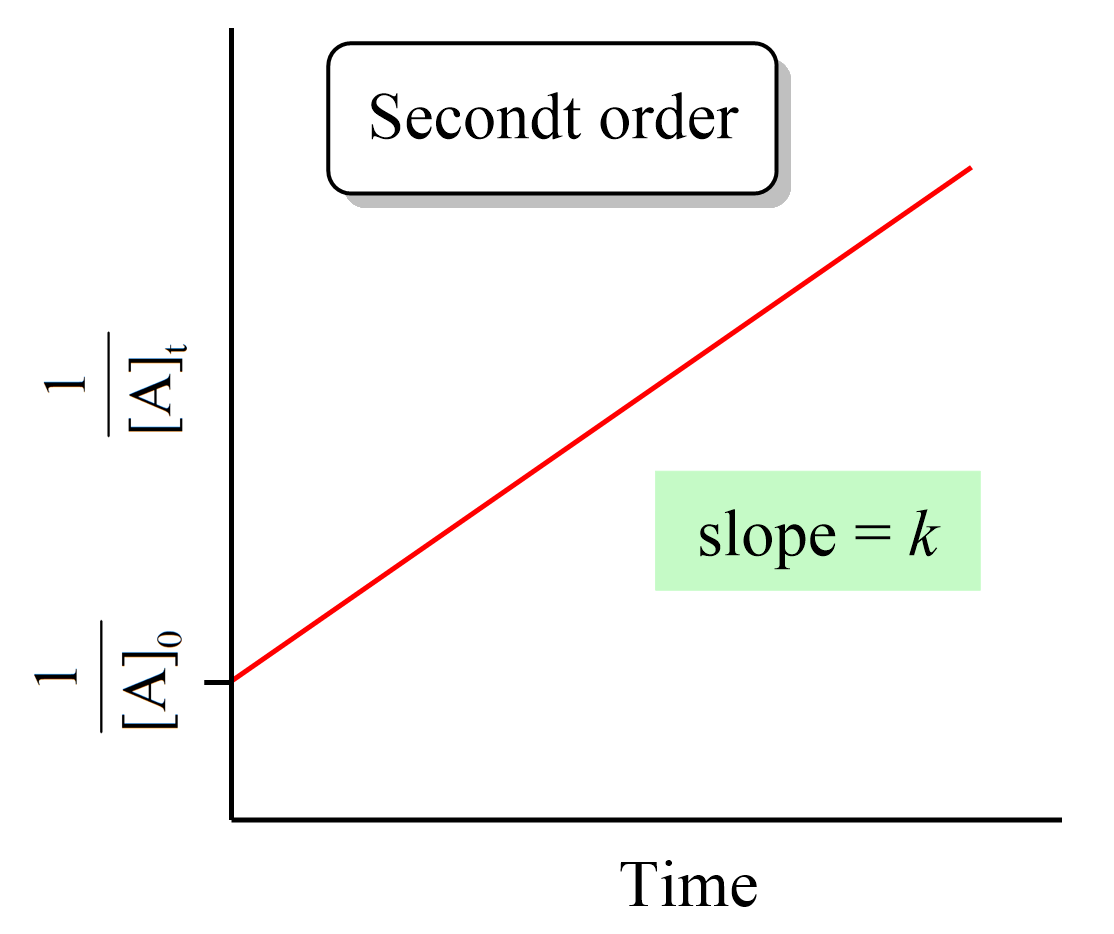
If we plot the concentration instead of its reciprocal, an exponential decrease will be obtained rather than a straight line. And this is an important strategy for determining the order of a reaction because the straight line of each order is obtained with the plot of different data such as the concentration, the log, or the reciprocal of it. This also is covered in a separate article, so be sure to check it out as determining the reaction order is a very common type of question in kinetics.
The Applications of the Integrated Rate Laws?
So, we have obtained the equation and the graph for the integrated rate laws, and the question is what do we use them for?
There are two main applications, at least two main types of problems, you will be given in your class based on the integrated rate laws:
- One is determining the concentration of a reactant or product at a certain point of the reaction when the reaction order is provided.
- The second is actually determining the rate law based on the data on how the concentration changes with time.
Let’s do an example of determining the concertation of a reactant when the reaction order is given.
Example:
Molecular iodine can be formed when iodine atoms combine in the gas phase:
I(g) + I(g) → I2(g)
Considering it is a second-order reaction with k = 7.0 x 109/M · s, calculate the concentration of I(g) after 150 seconds if its initial concentration was 0.048 M.
Solution:
First, write down what is given and what needs to be determined:
[A]0 = 0.048 M
k = 7.0 x 109/M · s
t = 150 s
___________________
[A]t = ?
The integrated rate low for second-order reactions is:
\[\frac{1}{{ {{[A]}_t}}}\; = \;kt\; + \;\frac{1}{{ {{[A]}_0}}}\;\;\]
We can now enter the numbers and solve for [A]t:
\[\frac{1}{{ {{[A]}_t}}}\; = \;\left( {7.0\, \times \,{{10}^9}/M\cdots} \right)\, \times 150\,s\; + \;\frac{1}{{ 0.048\,M}}\;\;\]
\[\frac{1}{{ {{[A]}_t}}}\; = \;1.05\, \times \,{10^{12}}\;\;\]
[A]t = 9.52 x 10-13 M
This insignificant concentration indicates that there is almost no I(g) left after 150 s of the reaction, and this is because the rate constant is very large.
The Half-Life of Second-Order Reactions
The half-life (t1/2) of a reaction is the time required for the concentration of a reactant to drop to one-half of its initial value. It depends on the order of the reaction, and it is obtained from the corresponding integrated rate law.
Like the first-order reactions, the half-life of second-order reactions is derived from the integrated rate law:
\[\frac{1}{{ {{[A]}_t}}}\; = \;kt\; + \;\frac{1}{{ {{[A]}_0}}}\;\;\]
Replacing [A]t with 1/2[A]0, we get:
\[\frac{1}{{ {\textstyle{1 \over 2}}{{[A]}_0}}}\; = \;k{t_{1/2}}\; + \;\frac{1}{{ {{[A]}_0}}}\;\;\]
And now we can rearrange the equation for the half-life:
\[k{t_{1/2}}\, = \,\frac{2}{{ {{[A]}_0}}}\; – \;\frac{1}{{ {{[A]}_0}}}\;\;\]
\[{t_{1/2}}\, = \,\frac{1}{{ k{{[A]}_0}}}\;\;\]
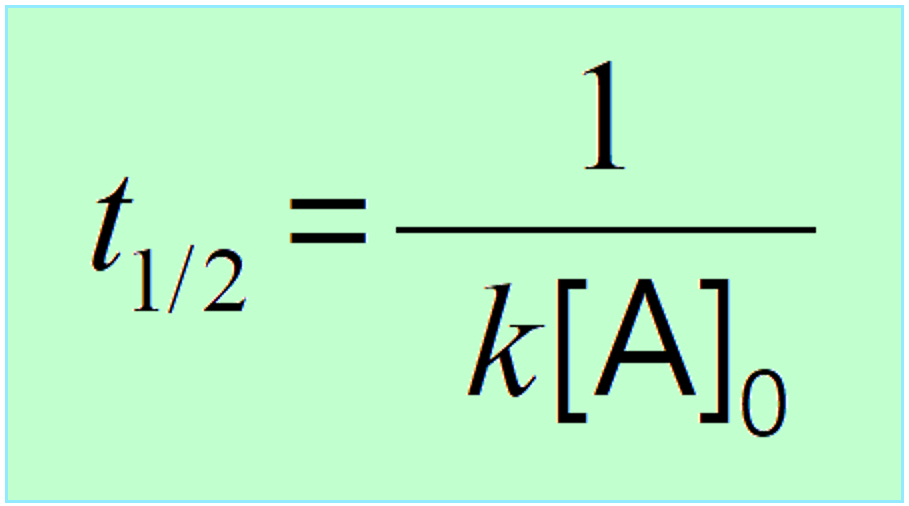
This indicates that the half-life of a second-order reaction depends on the initial concentration of the reactant, and the lower the initial concentration, the longer the half-life.
To understand this correlation, we need to remember that a second-order reaction occurs when two reactant molecules collide with sufficient energy and proper orientation. Therefore, the higher the concentration, the higher the probability of these collisions, the faster the rate, and therefore, the shorter the half-life.
The opposite is also true, the lower the initial concentration, the lower the probability of the collisions and thus, the longer the half-life.
Below is a summary of what we learned about the half-life of a reaction and its correlation with the concentration for a first-, second-, and zero-order reactions:
Notice that in all cases, the half-life depends on the rate constant which appears in the denominator. And this indicates that the faster the reaction, the shorter its half-life.
Check Also
- Reaction Rate
- Rate Law and Reaction Order
- How to Determine the Reaction Order
- Integrated Rate Law
- The Half-Life of a Reaction
- Half-Life and Radioactivity Practice Problems
- First-Order Reactions
- Determining the Reaction Order Using Graphs
- Units of Rate Constant k
- How Are Integrated Rate Laws Obtained
- Activation Energy
- The Arrhenius Equation
- Chemical Kinetics Practice Problems


Third rate order derivation