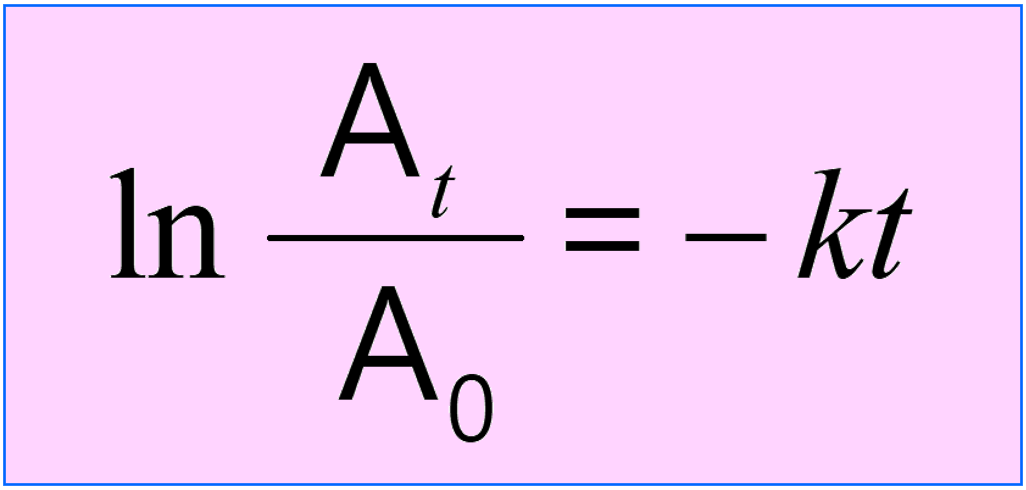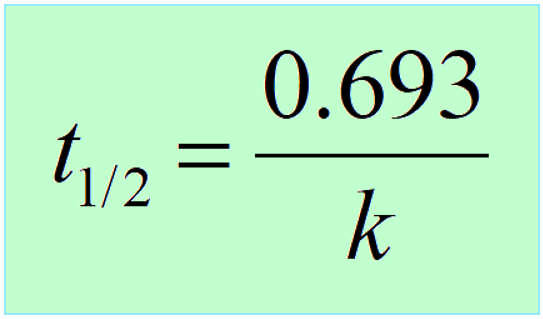In these practice problems, we will work on the kinetics of radioactive reactions. Most often, in chemistry at least, you will be asked to determine the activity, quantity, the decay rate of radioactive isotopes, the time required to drop the activity to a certain level, or apply those to techniques such as carbon dating for calculating the age of ancient objects.
For all of these, there are a few key concepts and main formulas you will need to know or be able to use if they are provided.
1) Remember that nuclear reactions follow the rules of first-order reactions. You are going to need the integrated rate law of first-order reactions:
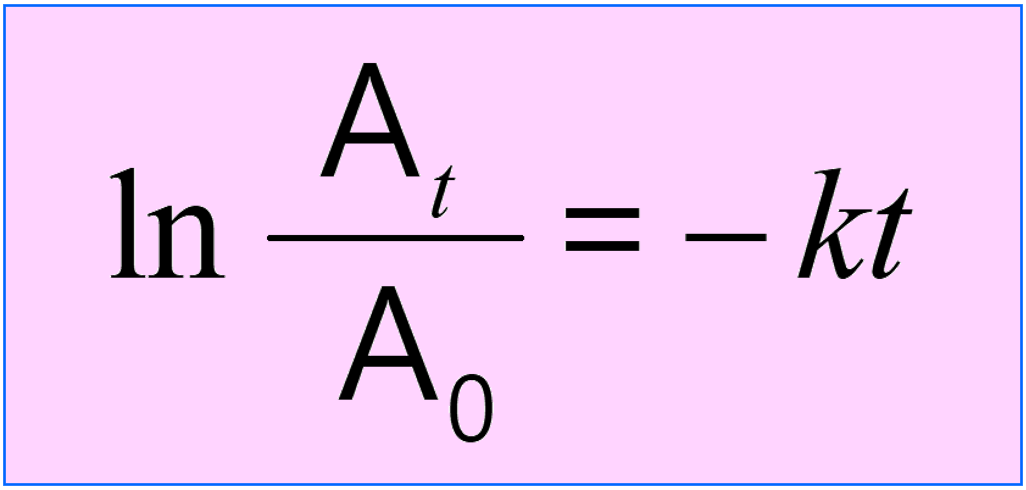
where At is the current activity, A0 is the initial activity, k is the rate (decay) constant, and t is the time for which the decay is measured.
It is important to remember that instead of activity (A), it can be the mass (m), moles, number of atoms (N), etc.
This formula is also used in carbon (or other elements) dating where we usually need to calculate t based on the initial activity (15.3 cpm/g C) and the half-life (5730 years) of 14C.
2) Remember, the activity is the number of disintegrations per given time, and this, in turn, can be calculated using the differential rate law for first-order reactions:

N here is the number of atoms (nuclei) and you will need to calculate in order to determine the activity of the nuclei.
Essentially, activity (A) is the rate of radioactive processes.
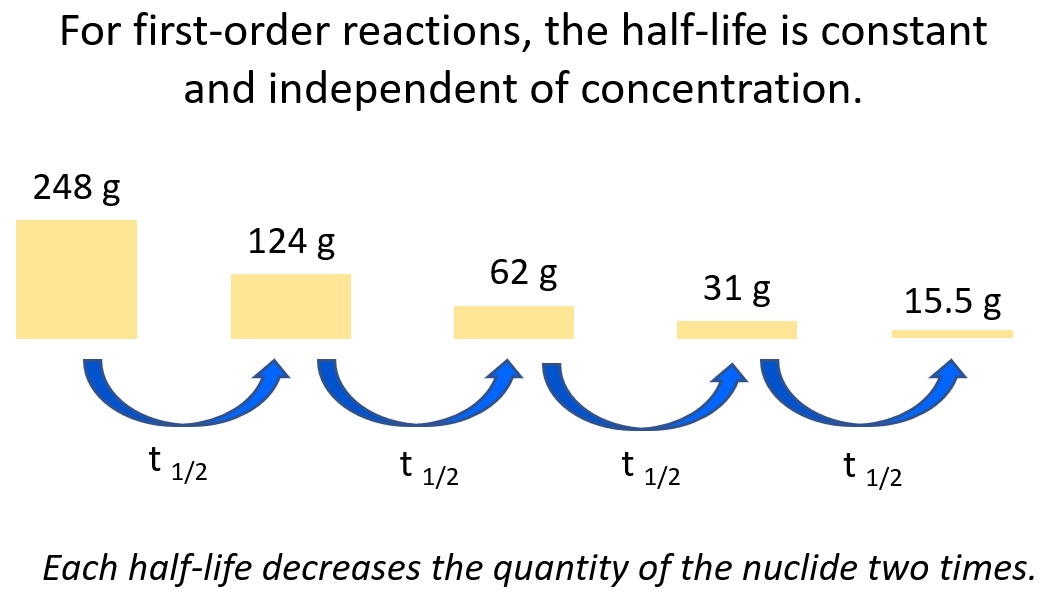
3) Another key component is the half-life, which, remember is constant for first-order reactions, and is correlated to the rate constant of the process:
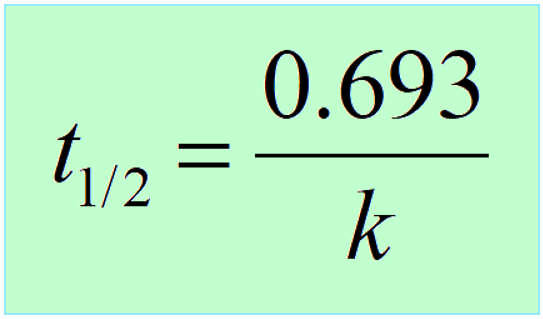
When solving half-life, or kinetics problems on nuclear reactions, there is often this initial lag when you don’t know where to start. A great strategy is to write down the quantities given in the problem, and the unknown next to them. After this, remember, most questions are going to be around these equations, so try to use them to find the link between the known and unknown in the problem.
Check Also
1.
Determine the half-life of a radioactive nuclide if its rate constant is 1.4 x 10-3 h-1.
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
2.
What is the rate (decay) constant for the beta decay of a radioactive nuclide if the half-life is 12.3 years?
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
3.
A radioactive isotope has a half-life of 14 days. How many grams of a 248-g sample remains after 56 days?
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
4.
A 2.34 g sample of radioactive isotope with a half-life of 4.6 days was obtained from a mine. How many grams of the isotope remains after 8.5 days?
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
5.
The initial activity of a radioactive sample was found to be 1564 disintegrations per minute. After 7.50 h the activity dropped to 895 disintegrations per minute. What is the half-life of the nuclide?
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
6.
A sample of a radioactive isotope has an initial activity of 35 dis/min. 2.00 hours later the activity is measured to be 16 dis/min. Determine how many atoms of the radioisotope were in the sample initially.
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
7.
An archaeological sample gives 4.80 disintegrations of 14C per minute per gram of total carbon. How old is the sample if the initial decay rate of 14C is 15.3 cpm/g C, and its half-life is 5730 years?
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
8.
How old is an ancient painting with a 14C activity of 7.60 cpm/g if the initial decay rate of 14C is 15.3 cpm/g C, and its half-life is 5730 years?
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
9.
A wooden tray discovered by a group of archeologists has a 14C activity that is 73% of the current 14C activity. How old is the tray?
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
10.
The activity of 400. mg sample of 14C carbon collected from an ancient cloth is 145 disintegrations per hour. How old is the cloth if the activity of a current 1.00-g sample of carbon is 921 disintegrations per hour?
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
11.
The bones of a camel were found to have 14C activity of 3.40 dis/min · g carbon. Determine, approximately, how long ago the animal lived given the initial decay rate of 14C is 15.3 cpm/g carbon, and its half-life is 5730 years?
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
12.
What is the activity of a 1.50-g sample of Molybdenum-93 given the half-life is 4000. years? Express your answer in becquerel (Bq) which is the activity equivalent to 1 disintegration per second.
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
13.
The half -life of 60Co is 5.3 years. What will be the activity of a 60Co sample in 47 years if the current activity is 7864 dis/min?
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
14.
A sample of a radioactive nuclide has an activity of 1850 disintegrations per minute. After 5.0 h the activity dropped to 1065 disintegrations per minute. Determine the half-life of the radioisotope.
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
15.
The half-life of Np-239 is 2.40 days. How many decay events will a 1.80-g sample of this nuclide produce in the first second assuming the atomic mass is 239 u?
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
16.
The half-life of 90Sr is 20.0 years. How long does it take for a sample of 90Sr to reach 25% of the initial amount?
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
17.
Fluorine-18 (t1/2 = 109 min) is commonly used in PET scans to locate certain cells. Can the PET scan be done 5 hours after the administration if the minimal amount of fluorine-18 is 20% of its initial value?
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
18.
A patient was given 1.80-mg dose of Iodine-131 to treat a thyroid disease. How long will it take to decrease the amount of I-131 to 0.400 mg if the half-life of the nuclide is 8.0 days? Assume the nuclide is not removed from the body by other means.
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
19.
In a certain experiment, 1.60 g of 18F needed to be used for imaging specific sells. The source for this nuclide is NaF which takes 3 hours to be delivered. Given the half-life of 18F is 109 min, what mass of NaF must be ordered from the supplier?
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
20.
Thallium-201 is in medical imaging for nuclear cardiology and certain cells. How many grams of the 201Tl nuclide can be delivered to the hospital from a nuclear facility that is 350 miles away if a 30.0-g sample is transported in a truck that drives at 65 mi/h. The half-life of 201Tl is 73.1 hours.
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.