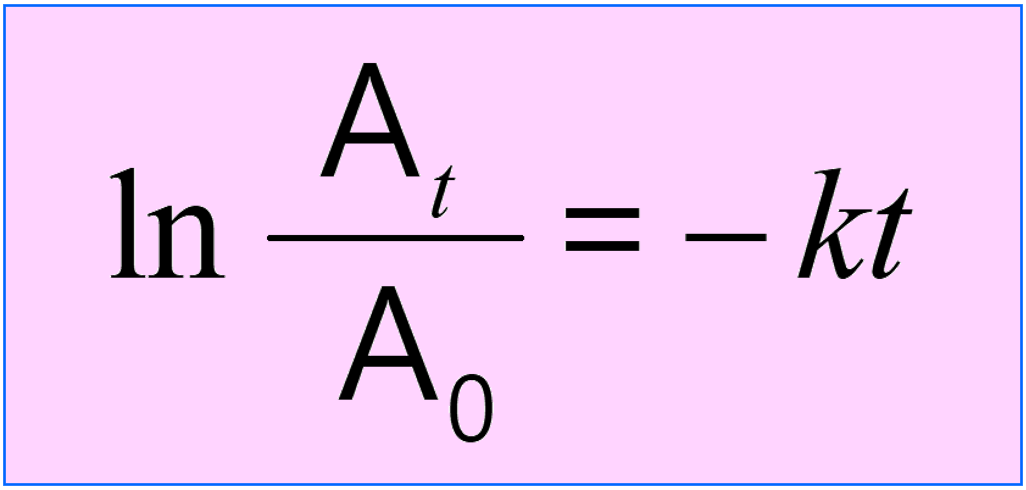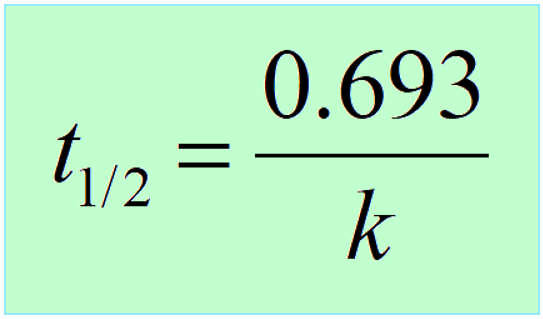Carbon dating is a technique that measures the age of ancient objects containing carbon.
The 14C isotope of carbon is radioactive and is only accumulated in living organisms.

Once dead, the amount of 14C, and thus its ratio to the 12C decreases which results in decreasing the radioactivity of the sample.
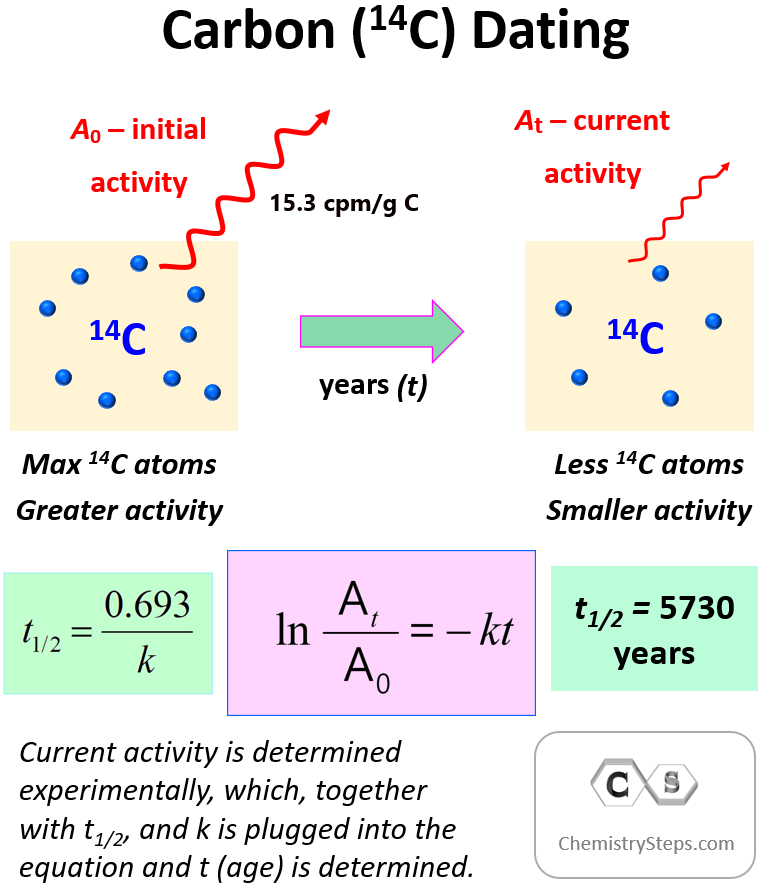
To determine the age of the sample, we need to compare the initial (15.3 cpm/g C) and current activity of 14C using the integrated rate law of first-order reactions.
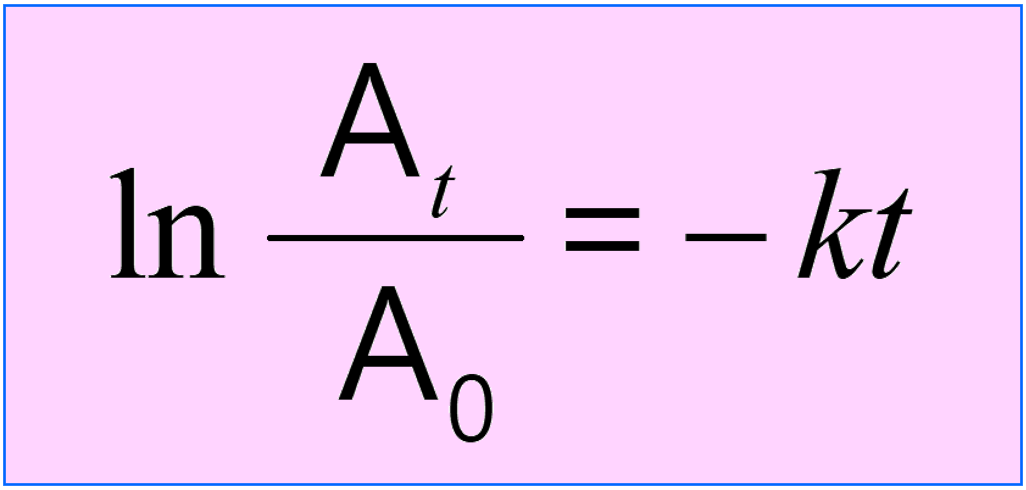
where At is the current activity, A0 is the initial activity, k is the rate (decay) constant, and t is the time for which the decay is measured.
It is important to remember that instead of activity (A), it can be the mass (m), moles, number of atoms (N), etc.
Another key component is the half-life, which, remember is constant for first-order reactions, and is correlated to the rate constant of the process:
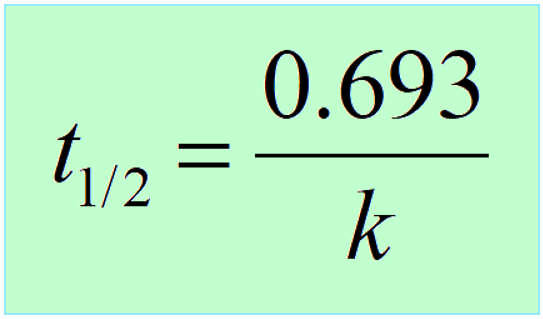
Carbon dating is a specific example of using the kinetics of nuclear reactions. For a more comprehensive list of the half-life, and other features of nuclear reactions, check the following set of practice problems:
Here is a 73-question, Multiple-Choice Quiz on Nuclear Chemistry:
Free

1.
An archaeological sample gives 4.80 disintegrations of 14C per minute per gram of total carbon. How old is the sample if the initial decay rate of 14C is 15.3 cpm/g C, and its half-life is 5730 years?
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
2.
How old is an ancient painting with a 14C activity of 7.60 cpm/g if the initial decay rate of 14C is 15.3 cpm/g C, and its half-life is 5730 years?
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
3.
A wooden tray discovered by a group of archeologists has a 14C activity that is 73% of the current 14C activity. How old is the tray?
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
4.
The activity of 400. mg sample of 14C carbon collected from an ancient cloth is 145 disintegrations per hour. How old is the cloth if the activity of a current 1.00-g sample of carbon is 921 disintegrations per hour?
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
5.
The bones of a camel were found to have 14C activity of 3.40 dis/min · g carbon. Determine, approximately, how long ago the animal lived given the initial decay rate of 14C is 15.3 cpm/g carbon, and its half-life is 5730 years?
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.