Despite some fundamental differences between chemical and nuclear reactions, they both share a common feature which you heard so many times – the equation must be balanced!
For chemical reactions, the equation is balanced by equalizing the number of given atoms on both sides of the equation. For example:
Ca(AlO2)2 + 8HCl → 2AlCl3 + CaCl2 + 4H2O
So, how do we balance a nuclear equation?
You need to keep in mind that the sum of the mass numbers and atomic numbers are equal on both sides of the equation.
In other words, the sum of the superscripts and subscripts on both sides of the equation must be equal. For example:

This is the equation for the alpha decay of the uranium-238 isotope to the thorium-234 isotope. The sum of the protons on the right side (90 + 2) is equal to the atomic number of uranium, and the sum of the mass numbers of Th and α (234 + 4) is equal to the atomic mass of the 23892U isotope.
This principle applies to all the radioactive decay and transformations such beta decay, positron emission, and electron capture.
You check this article for the details of these processes, but here is a summary for these radioactive processes which we are going to use when balancing different nuclear reactions:

You need to know what each of these terms mean because balancing a nuclear equation often means identifying the daughter nuclide (product) of the reaction. So, remember the following definitions from the atomic structure.
- Proton (p or p+) – a subatomic particle with a positive electric charge of 1+.
- Neutron (n or no) – a neutral subatomic particle slightly heavier than a proton.
- Electron (e–) – a subatomic particle with a negative electric charge of 1-.
- Positron – the antiparticle of the electron as it has the same mass as an electron, but the opposite charge
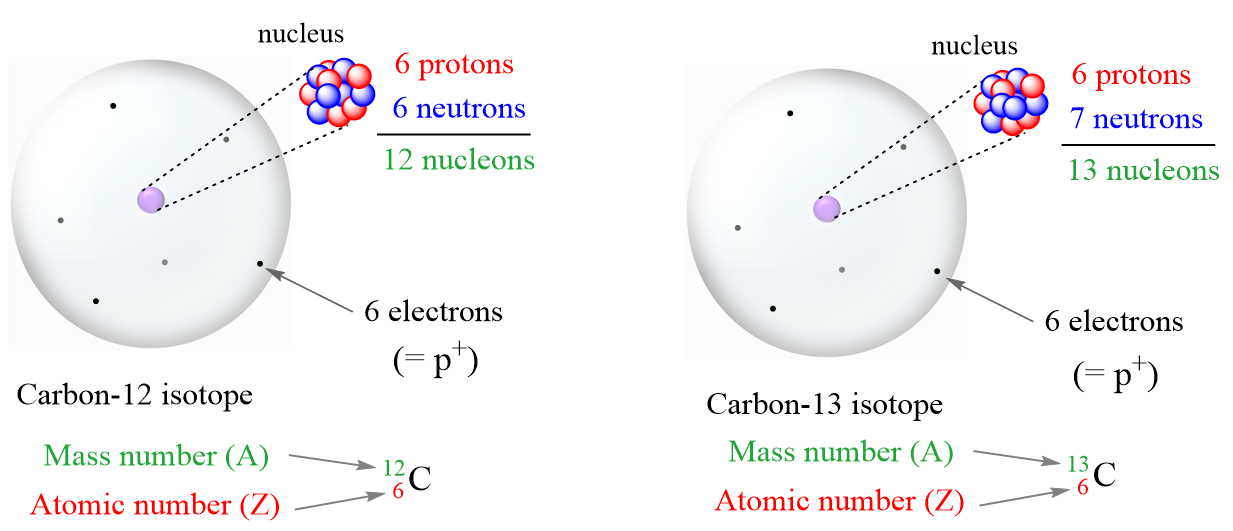
- Atomic number (Z) – the number of protons in an atom. Always the same for the given element
- Mass number (A) – the sum of the number of neutrons and protons
- Every atom has an equal number of electrons and protons, so atoms have no net
- electrical charge.
- Isotopes– atoms with the same number of protons (atomic number) but different numbers of
- Because of a different number of neutrons, isotopes have different mass numbers.
- Nucleons – a general term for both protons (p) and neutrons (n)
- Nuclide – the nucleus of a given isotope
Before addressing the specific types of nuclear reactions and strategies to balance them, let me mention right from the beginning that balancing nuclear equations means identifying the unknown particle(s) in the reaction. This is because most of the time, we do not have coefficients in front of the nuclides since we do not have the same element appearing on both sides of the equation. Instead, when balancing nuclear equations, we need to identify the correct particle(s) to make sure the sum of the atomic numbers and mass numbers are balanced.
Balancing Equations for Alpha (α) Decay
For example, let’s say the question asks you to identify the daughter nuclide for the alpha decay of 224Ra.
Now, if you don’t know what alpha decay means then you are stuck in this problem. In that case, feel free to go over the main radioactive pathways in this article before proceeding forward.
Remember, alpha (α) decay occurs when an unstable nucleus loses a particle composed of two protons and two neutrons. These are called alpha particles symbolized as α, 24α, or 24He2+ which are identical to the helium-4 nuclei.
Therefore, we know that the mass number and the atomic number of 224Ra are going to decrease. We can start by writing the symbol of 224Ra on the left side of the nuclear equation and adding an alpha particle on the right side of the equation. Meanwhile, look up the atomic number of Ra in the periodic table, and write it as well since it will help identify the daughter nuclide:
22488Ra → X + 42He
To determine the number of protons of the daughter nuclide, we subtract 2 (the two protons of the alpha particle) from 88 (the atomic number of Ra):
X (atomic number) = 88 – 2 = 86
Therefore, the atomic number of the daughter nuclide is 86, and using the periodic table, we determine that it is radon (Rn):
22488Ra → 86Rn + 42He
At this point, we only need to determine the mass number of the specific Rn isotope that is formed in this reaction.
22488Ra → ?86Rn + 42He
This, again, is determined based on the fact that the sum of the mass numbers must be balanced on both sides of the nuclear equation. Therefore, the mass number of Rn is the difference between those of 22488Ra and 42He:
M (86Rn) = M (22488Ra) – M (42He)
M (86Rn) = 224 – 4 = 220
Therefore, the balanced equation for the alpha decay of 22488Ra can be written as:
22488Ra → 22086Rn + 42He
Balancing Equations for Beta (β) Decay
Beta (B) decay is the emission of an electron from an unstable nucleus. For example, carbon transforms into nitrogen when one of the neutrons in the 14C nucleus is converted into a proton because losing a negatively charged particle with negligible charge converts a neutral particle into a positively charged particle. Therefore, there is a new atom formed with 7 protons which corresponds to the 14N isotope.
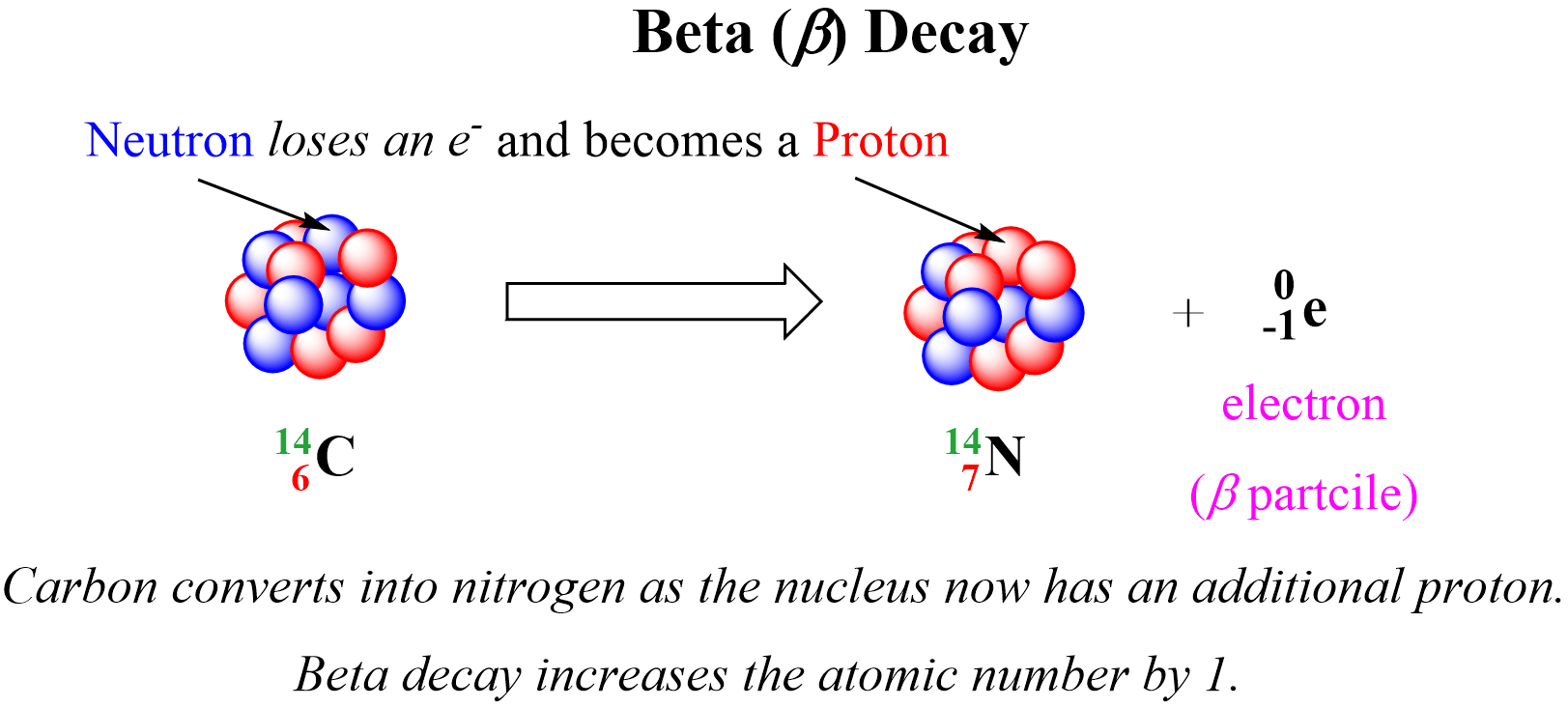
We can write a balanced nuclear equation for this reaction as:

Let’s do a practice example: Identify the product X by writing a balanced nuclear equation:
13755Cs → 13756Ba + X
Because the mass number is the same on both sides of the equation, X must have a mass number of 0. One the other hand, the atomic number of the product is 1 more than that of the reactant which there is an additional proton formed during this process. Remember, a proton is formed when a neutron loses an electron, and therefore, X is a beta particle. Thus, the balanced equation would be:
13755Cs → 13756Ba + 0-1β
Balancing Equations for Positron Emission
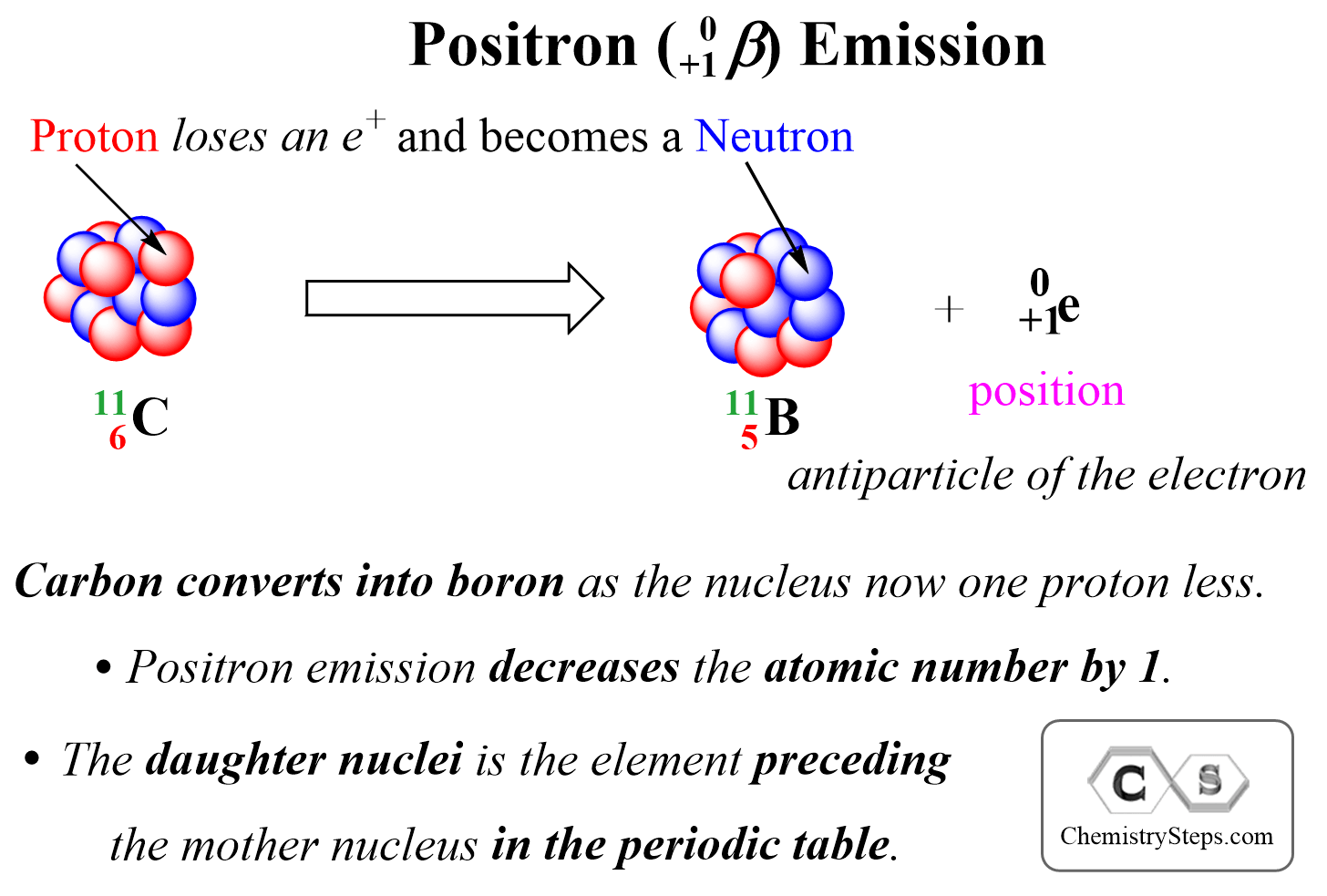
Positron Emission is the ejection of a positron ( 0+1β) from a neutron-poor nucleus. Positron is a high-velocity particle emitted from the nucleus and it has the same mass as an electron, but the opposite charge, it is the antiparticle of the electron.
We can visualize positron emission as shown below:
For example, write the nuclear equation for the position emission of the 3015P isotope:
3015P → X + 0+1β
Positron is a positively charged particle emitted from a proton, and therefore, it decreases the atomic number by 1 as one proton is converted into a neutron. Therefore, the product is going be an isotope of the element with the atomic number 14 which is Si.
3015P → 3014Si + 0+1β (or 0+1e)
Notice that the mass number does not change as protons and neutrons have almost identical masses.
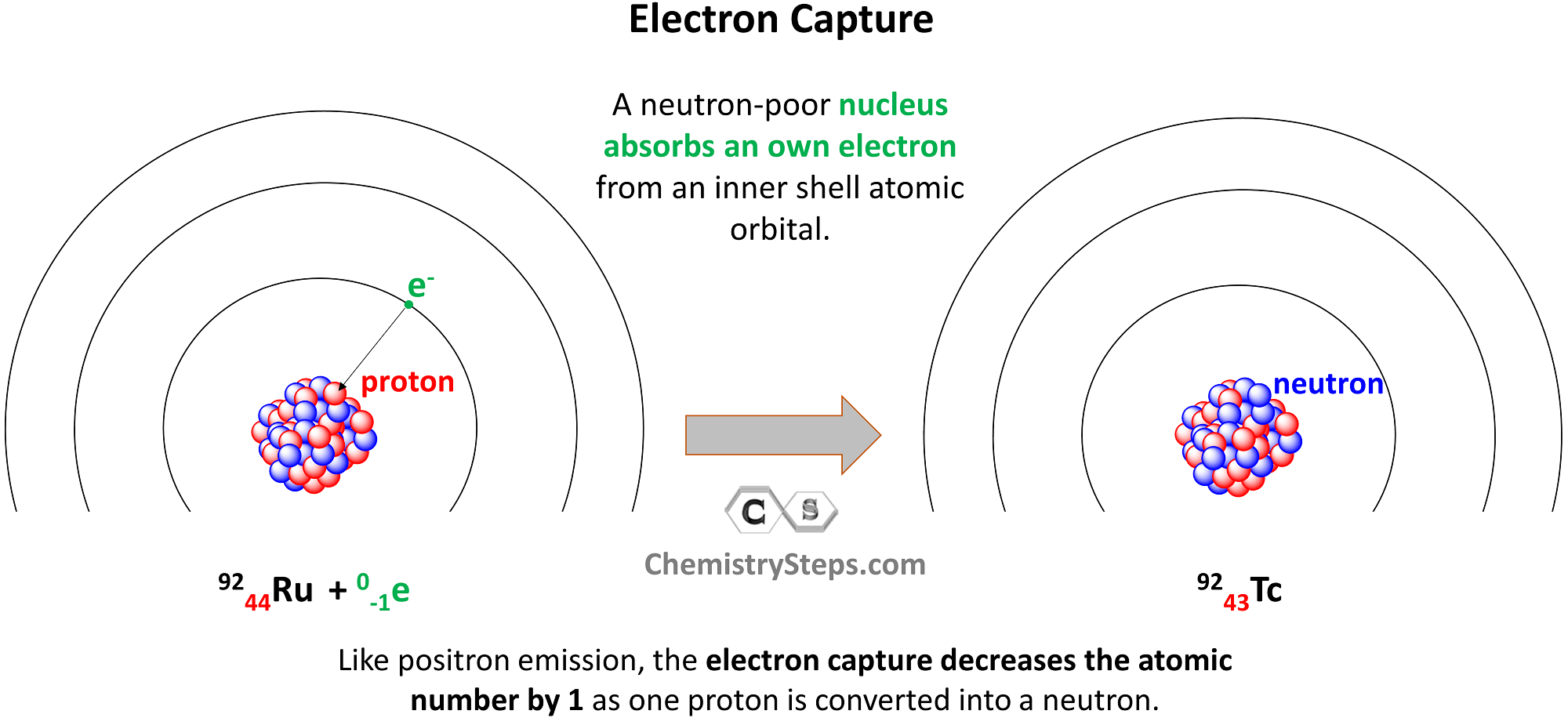
Balancing Equations for Electron Capture
Electron capture occurs when a neutron-poor nucleus absorbs an own electron from an inner shell atomic orbital. Like positron emission, the electron capture decreases the atomic number by 1 as one proton is converted into a neutron.
For example, Ru-92 undergoes electron capture, converting into Tc-92:
Let’s a practice example of electron capture as well. Identify the product X in the following equation for the electron capture of the Au-195 isotope:
19579Au + 0-1e→ X
Capturing an electron converts one of the protons to a neutron, and therefore, the atomic number of the daughter nucleus is going to be 78. From the periodic table, we determine that it is platinum:
19579Au + 0-1e→ ?78Pt
At this point, we are only missing the mass number of Pt, and since electron capture does not change it because the proton and neutron have nearly identical masses, we can write the balanced nuclear equation as:
19579Au + 0-1e→ 19578Pt
Other Nuclear Reactions
Some nuclear reactions do not occur by themselves, external triggers such as bombarding their nuclei with appropriate particles can facilitate processes like nuclear fission when the parent nuclide is split into other elements.
For example, the U-235 nuclide can be split into isotopes of Ba and Kr when bombarded with neutrons:
23592U + 10n→ 14056Ba + 9336Kr + 3 10n + energy
Notice that despite looking more complex than the reactions we discussed earlier, the nuclear equation is balanced as the sum of the atomic numbers and the mass numbers are equal on both sides of the equation. For the sum of the atomic numbers on the left, we have 92 + 0 = 92, and on the left side is 56 +36 + 0 = 92. The sum of the mass numbers on the left is: 235 +1 = 236, and on the right side, it is 140 + 93 + 3 x 1 = 236.
Practice Problems On Radioactive Decay and Nuclear Reactions
Use this summary of radioactive processes and how they affect the number of protons and neutrons in the nucleus to solve the practice problems on balancing nuclear reactions such as alpha decay, beta decay, positron emission, electron capture, nuclear fission, and nuclear fusion.

Remember, out of all the radioactive processes discussed today, it is only the alpha decay that decreases the number of protons and neutrons and, as a result, the atomic mass of the daughter nuclide also decreases.
In position emission and electron capture, the number of protons decreases by one and that of neutrons increases by one because one proton is converted into a neutron. Therefore, an isotope of the element preceding the mother nuclide in the periodic table is formed which has the same atomic mass.
In beta decay, a negatively charged particle (electron) is emitted from a neutron which converts into a proton, and therefore, the daughter nuclide is an isotope of the element that follows the mother nuclide in the periodic table.
Gamma radiation by itself does not change the number of protons or neutrons unless accompanied by another type of radioactive decay. So, unless there is another type of radioactive decay, gamma radiation does not alter the nuclide, and therefore, the mass number stays the same as well.
Here is a 73-question, Multiple-Choice Quiz on Nuclear Chemistry:
Check Also
- Alpha Particles, Beta Particles, and Gamma Rays
- Carbon Dating Practice Problems
- Half-Life and Radioactivity Practice Problems
- The energy of Nuclear Reactions
- Nuclear Binding Energy
- Nuclear Fission and Fusion
Practice
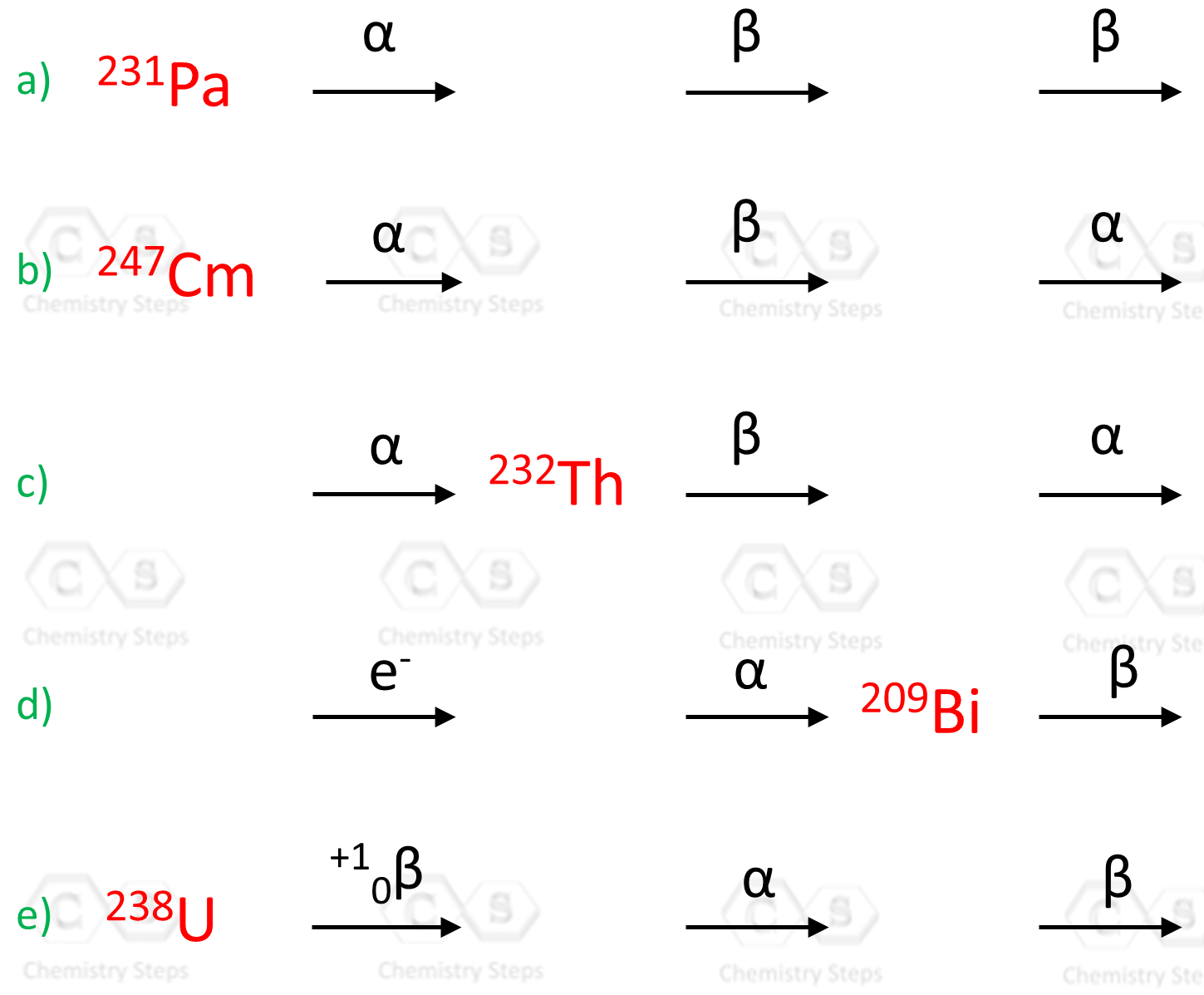
Complete the following nuclear equations and identify X in each reaction:

Identify the missing species in the following nuclear reaction: