In today’s post, we will talk about the atomic orbitals. So, first, what is an orbital? In a formal, quantum mechanical definition, orbitals are essentially probability distribution maps for electrons within atoms.

In a simpler version, think of orbitals as the place where electrons are located.

Now, about the types of orbitals and their relative energy levels. There are four types of atomic orbitals – s, p, d, and f. Each orbital has a characteristic shape shown below:

 

 

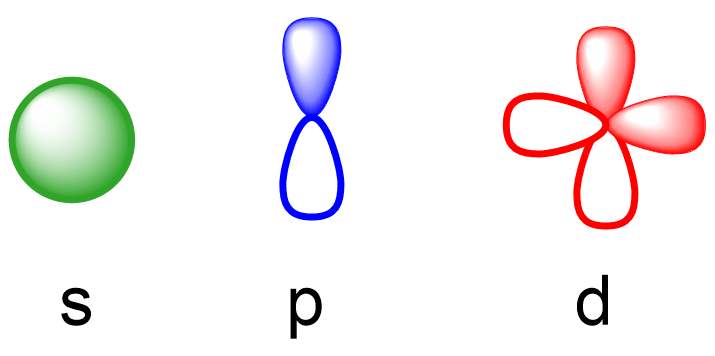
S orbitals have a spherical shape, p orbitals are dumbbell-shaped, d orbitals are shaped like a cloverleaf, and f orbitals are characterized by more complex shapes. You can also look up more detailed images for the shapes and orientation of atomic orbitals in your textbook.

 

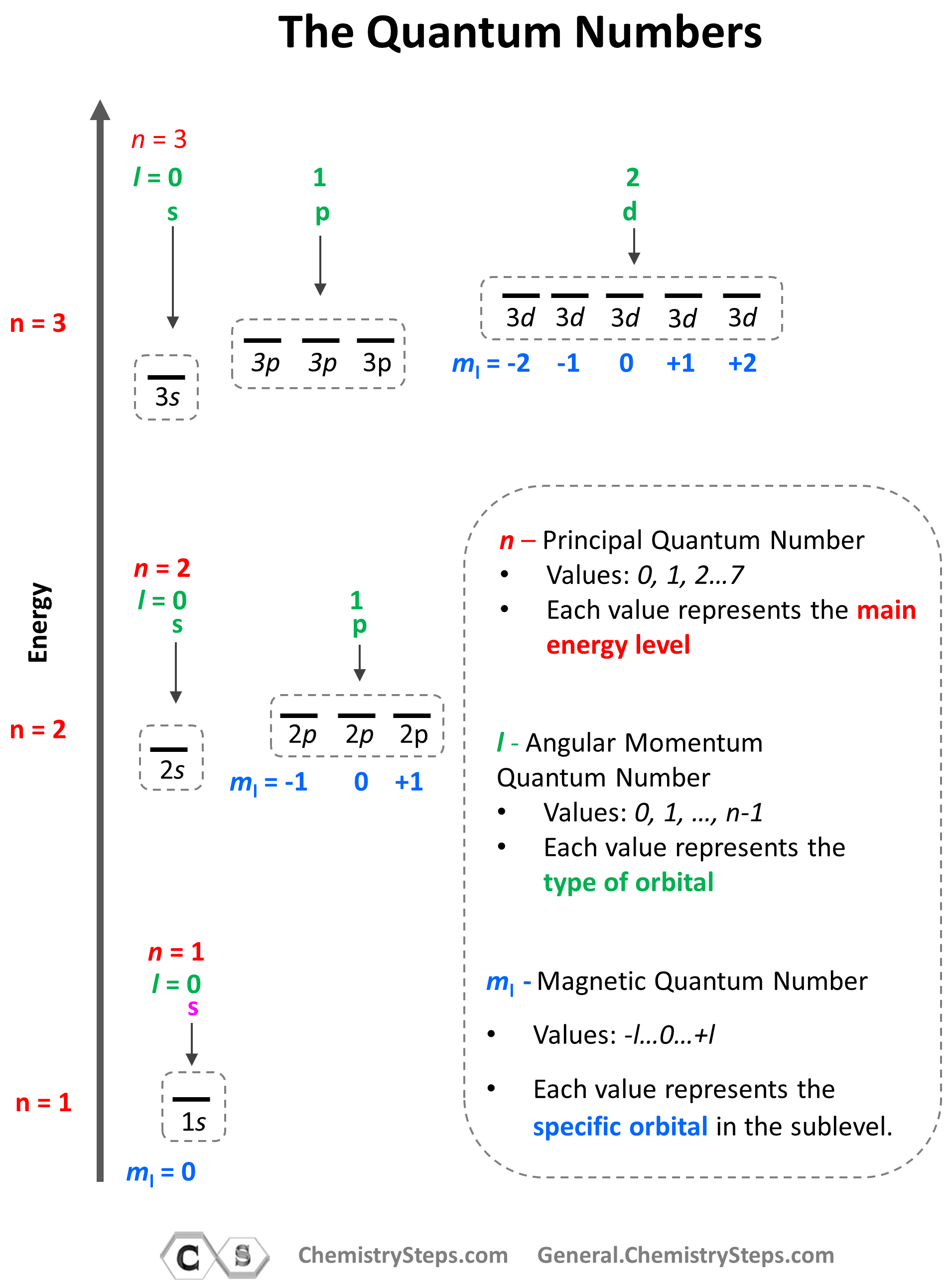
Principal Quantum Number (n)

What orbitals a given atom has, and in which ones the electrons are located, depends on the energy level of the atom. Remember, the energy level of the atom is given by the principal quantum number, n which can easily be determined based on the period (row)  the atom is located in the periodical table.

 

 

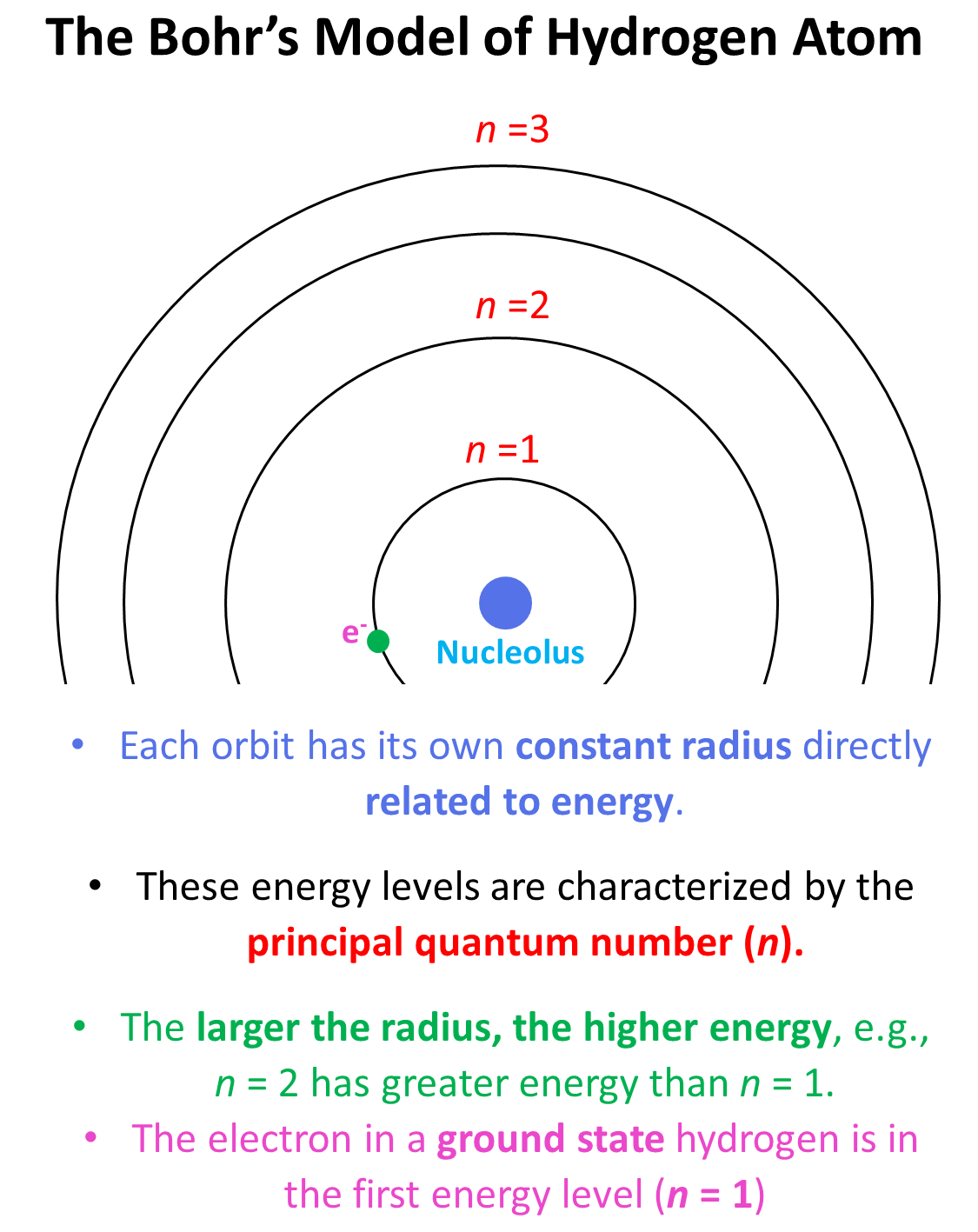
This is what we discussed about the Bohr model of hydrogen atom. There are orbits with fixed radius each associated with discrete energy, and this is described by the principal quantum number n.

 

 

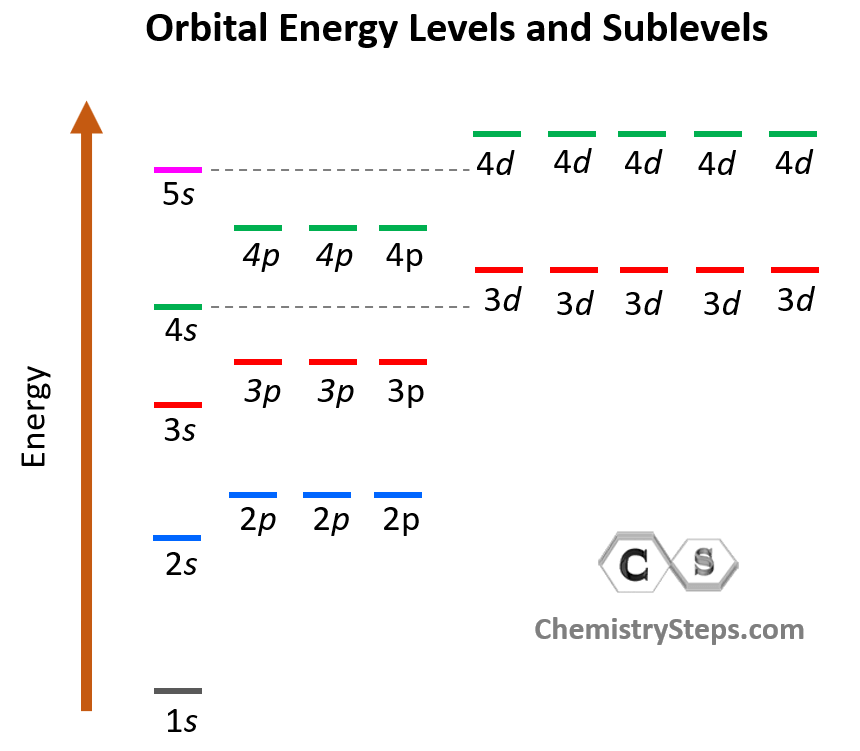
The number of types of orbitals matches the energy level: first energy level has only 1 (s) orbital, the second has two types – s and p, the third has three – s, p, and d, and the fourth level has all four types of orbitals – s, p, d, and f.

 

 

So, far we have talked about the main energy level. However, you should know, aside from the first energy level, each level also has sublevels. These are the types of orbitals – s, p, d, and f.

 

 

Angular Momentum Quantum Number (l)

The number of sublevels is given by the Angular Momentum Quantum Number – l. It takes values of 0, 1, … n-1. For example, for the second energy level, n = 2, and therefore, l = 0, 1 , so it can have two values, and therefore, the second energy level has two sublevels – s (l = 0) and p (l = 1).

 

Magnetic Quantum Number, m_l

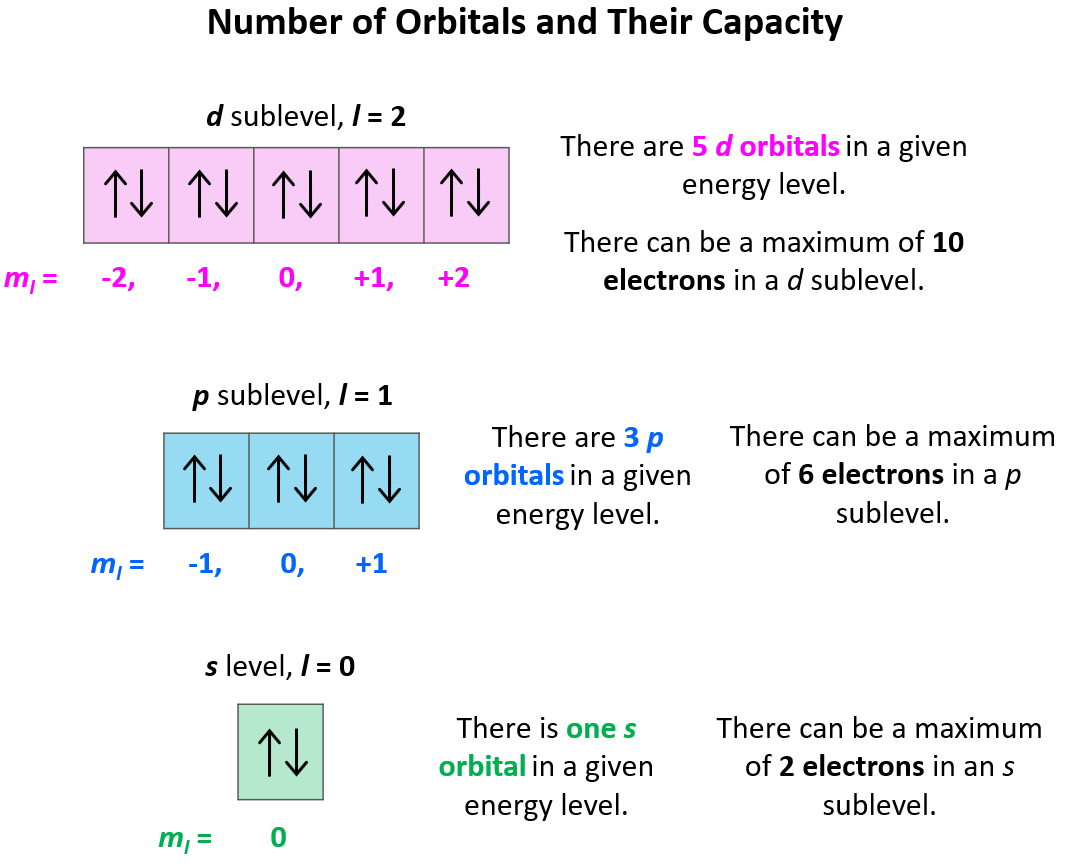
The next quantum number is the Magnetic Quantum Number, m_l which shows the number of orbitals in the sublevel. It takes values form –l to +l including the zero and all the integers. For example, when l = 2, we have d orbitals, and because m_l = -2, -1, 0, +1, +2, there are 5 orbitals in each sublevel.

The summary of quantum numbers including their meaning and values is given in the diagram below:

 

 

Notice again that within the same principal level, orbitals with a lower value of l have lower energy (E) and therefore, are filled first. So, for a given value of n:

 

E (s orbital) < E ( p orbital) < E (d orbital) < E ( f orbital)

 

Now, a few important things about the orbitals and their electron capacity. First, remember that each orbital, whether it is s, p, d, or f can accommodate two electrons at most.

We can see this in orbital diagrams where the orbitals are shown as boxes and electrons as arrows, we never put more than two arrows in the box. For example, boron has two electrons in each s orbital of the first and second levels, and one electron in the p sublevel.

 

 

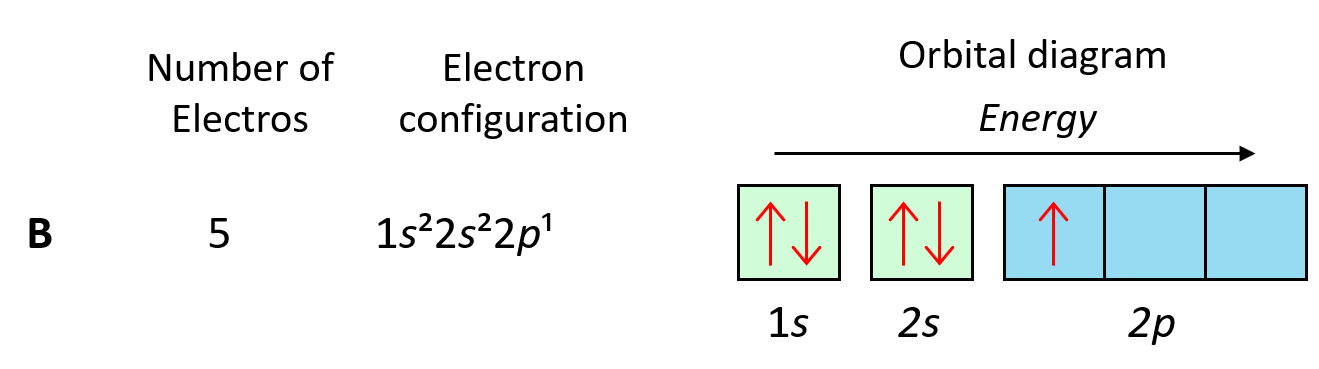
Do not worry about understating how we know where to put the electrons now because this is covered in a separate article about electron configurations.

Going back to the quantum numbers, specifically the Magnetic Quantum Number, m_l that shows how many types of orbitals we may have in the given sublevel, remember that there can only be 1 s orbital in the given energy level, 3 p orbitals, 5 d orbitals, and 7 f orbitals. And because each orbital can only take a maximum of two electrons, there can only be a maximum of two electrons in any s sublevel, 6 electrons in the p subshell, 10 in the d, and 14 in the f sublevel.

 

 

For example, which orbital is indicated by the following set of quantum numbers: n = 3, l = 2, m_l = 0?

Starting with the principal quantum number, we know that it is an orbital in the 3^rd energy level. L = 2, indicates a d orbital, and ml = 0 indicates the middle one of the five d orbitals.

 

 

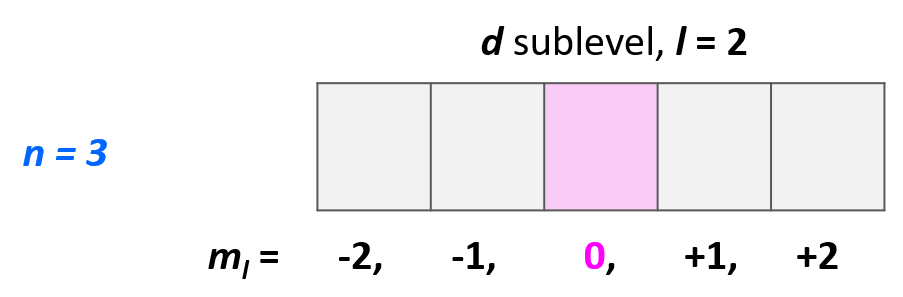
The Electron Spin Quantum Number (m_s)

The last quantum number is the Electron Spin Quantum Number (m_s) which shows the direction of the electron spin and depending on this may take a value of +1/2, represented by ↑, or -1/2, represented by ↓. Placing the direction of the arrow is important as the electrons in the same orbital may only have opposite spin.

This is the Hund’s rule, which states that electrons will fill all the degenerate orbitals (equal in energy) with parallel spins (both arrows up or down) first before pairing up in one orbital. We can also formulate it as the lowest energy configuration for an atom is the one having the maximum number of unpaired electrons within the same energy sublevel.

For example, in carbon the second electron in the p sublevel goes to the next (empty) p orbital rather than fitting in with the other electron:

 

 

Notice that placing the electron unpaired in the 3s orbital is also incorrect because, it is important to mention, that Hund’s rule applies to electrons in the same energy level. Check this article for more information and exceptions on the Hund’s rule, as well the Aufbau’s and Pauli’s exclusion principles.

 

Check this 95-question, Multiple-Choice Quiz on the Electronic Structure of Atoms including questions on properties of light such as wavelength, frequency, energy, quantum numbers, atomic orbitals, electron configurations, and more. 

 

Check Also

• Electron Configurations
• Electron Configurations of Ions
• Orbital Diagrams
• Aufbau’s Principle, Hund’s Rule, and Pauli’s Exclusion Principle
• Hund’s Rule
• Pauli Exclusion Principle
• Quantum Numbers (n, l, m_l, m_s)
• Bohr Model of the Hydrogen Atom
• Rydberg Formula
• The Photoelectric Effect
• Calculating The Energy of a Photon
• Ionization Energy
• Electron Affinity
• Energy, Wavelength, and Frequency Practice Problems