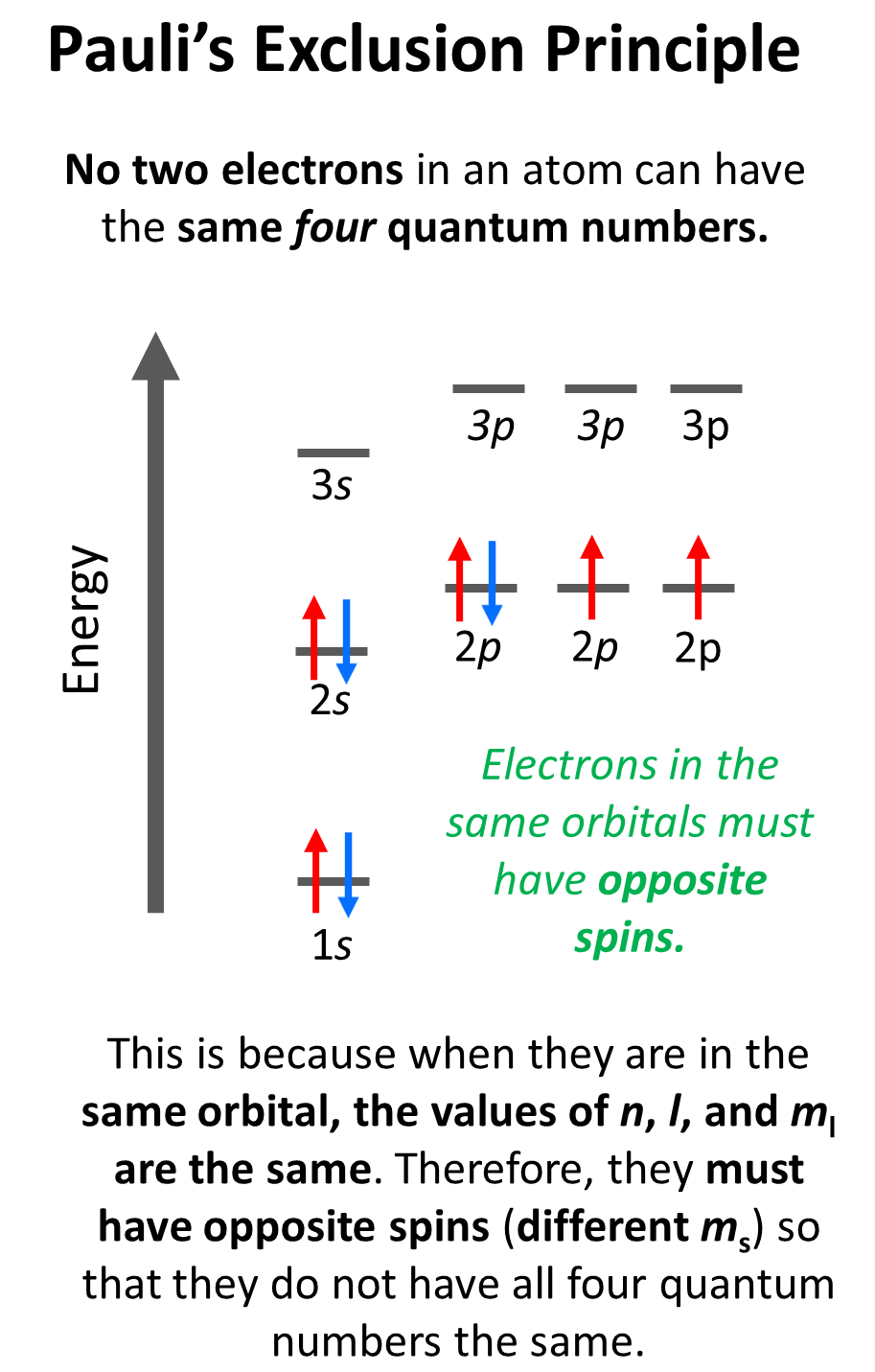
The Pauli’s exclusion principle states that no two electrons in an atom can have the same four quantum numbers. Now, what does this practically mean? Essentially, the implication of Pauli’s exclusion principle is that when two electrons are in the same orbital, they must have opposite spins. In other words, you should put the arrows representing the electrons in opposite directions.
For example, the electron configuration of boron is 1s22s22p1 which can be represented by orbital diagrams:
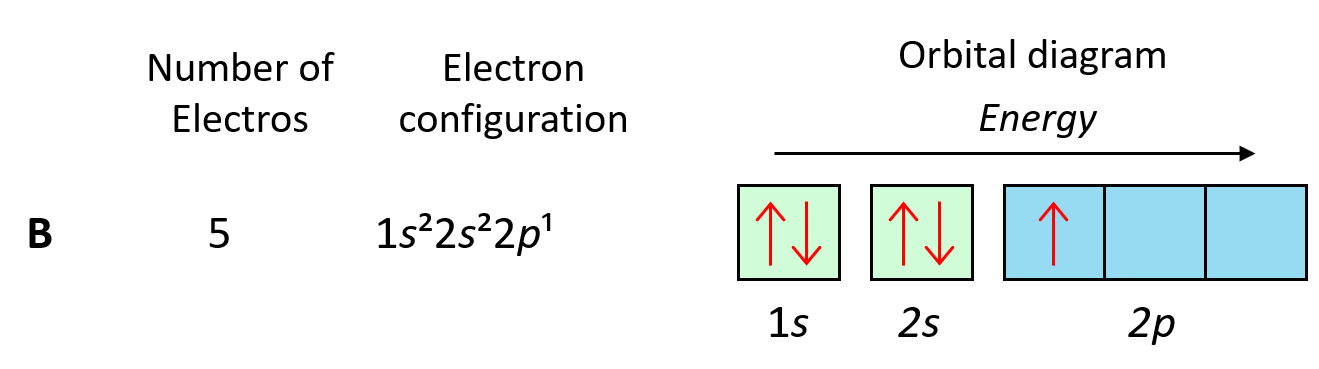
Notice that the two s orbitals have every two electrons and they have opposite spins. Remember, the spin is indicated by the spin quantum number, ms which can be either +1/2 (↑) or -1/2 (↓). The values of ms are assigned arbitrarily as we do not know if the first electron is +1/2 or -1/2, however, if we assign it +1/2, then the second must be -1/2 and vice versa. Conventionally though, we put the first arrow pointing up, but it has no scientific evidence, and maybe the other way around.
The one electron in the p orbital can also be pointing up or down.
Let’s also look at the electron configuration of the next element in the periodic table which is carbon, and therefore, the electron configuration will be 1s22s22p2. Here, you need to remember, that within the same sublevel, the electrons prefer to stay unpaired, and therefore, the electron goes to the next p orbital. This is the Hund’s rule, and we will talk about it in more detail in a separate post.

As we keep adding electrons, at some they will need to be paired in the p orbitals, and this again will be according to the Pauli exclusion principle. For example, oxygen has 4 electrons in the 2p sublevel, and therefore, two of them must be paired with opposite spins:
Quantum Numbers and Pauli Exclusion Principle
In the formal definition of Pauli’s exclusion principle, we said that no two electrons can have the same set of four quantum numbers ( n, l, ml, ms).
First, remember what quantum numbers indicate:
There are four quantum numbers that we are going to discuss:
- The Principal Quantum Number (n) – indicates the main energy level of orbitals and electrons
- The Angular Momentum Quantum Number (l) – indicates the energy sublevel, which is given by the type of the orbital (s, p, d, f)
- The Magnetic Quantum Number, (ml) – indicates the specific orbital within the energy sublevel
- The Electron Spin Quantum Number (ms) – shows the direction of the electron spin
So, one can visualize the information conveyed by quantum numbers getting more specific as we go from the principal quantum number to the spin quantum number:
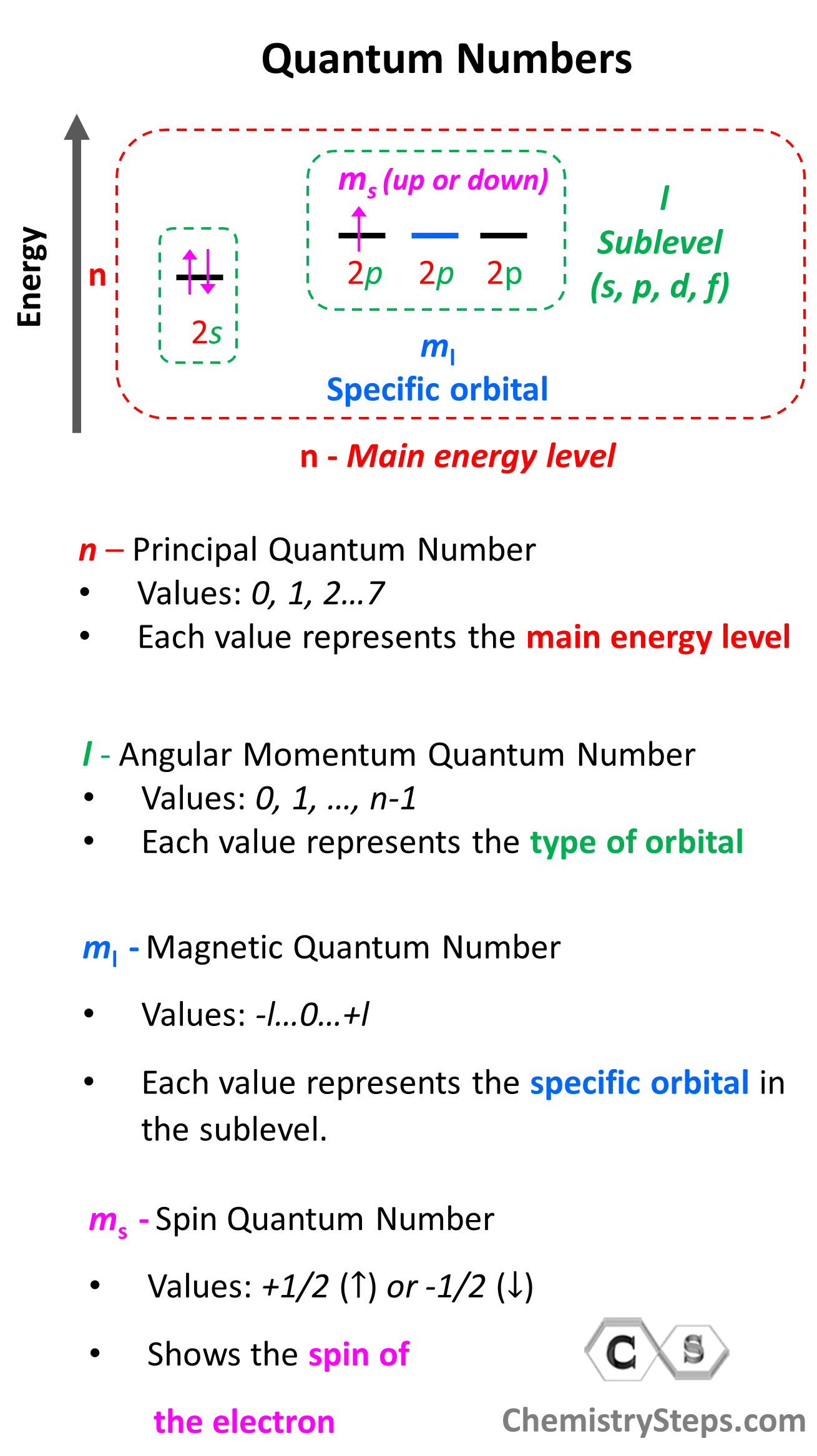
Notice that the first three quantum numbers (n, l, ml) describe the orbital of the electron(s) and the fourth (ms) describes its spin. Therefore, if two electrons are in the same orbital they must have the same first three quantum numbers, while the ms must be different.
For example, for the electrons of oxygen in a 2p orbital, n = 2, l = 1, and ml = –1, 0, or +1 (doesn’t matter which one because for two electrons in the same orbital, it will be identical). Therefore, the ms must be different (+1/2 or -1/2) in order not to violate Pauli’s exclusion principle.
An important consequence of the Pauli exclusion principle is that an atomic orbital can
accommodate a maximum of two electrons. Adding the third will place two arrows in the same direction regardless of how the first two are oriented to have opposing spins.
Check this 95-question, Multiple-Choice Quiz on the Electronic Structure of Atoms including questions on properties of light such as wavelength, frequency, energy, quantum numbers, atomic orbitals, electron configurations, and more.
Check Also
- Atomic Orbitals
- Electron Configurations
- Electron Configurations of Ions
- Orbital Diagrams
- Aufbau’s Principle, Hund’s Rule, and Pauli’s Exclusion Principle
- Hund’s Rule
- Quantum Numbers (n, l, ml, ms)
- Bohr Model of the Hydrogen Atom
- Rydberg Formula
- The Photoelectric Effect
- Calculating The Energy of a Photon
- Ionization Energy
- Electron Affinity
- Energy, Wavelength, and Frequency Practice Problems

