Energy and Atomic Structure
Remember, when discussing the Bohr’s model for the hydrogen atom, we saw that there are orbits with distinct energies that the electron can occupy. Each orbit has its own constant radius which is directly related to energy, and these energy levels are characterized by the principal quantum number (n) which is a whole number. Each energy level is represented as n1, n2, n3, and so on. The larger the radius, the higher energy, so n = 2 has greater energy than n = 1 and n = 3 has greater energy than n = 2, and so on.
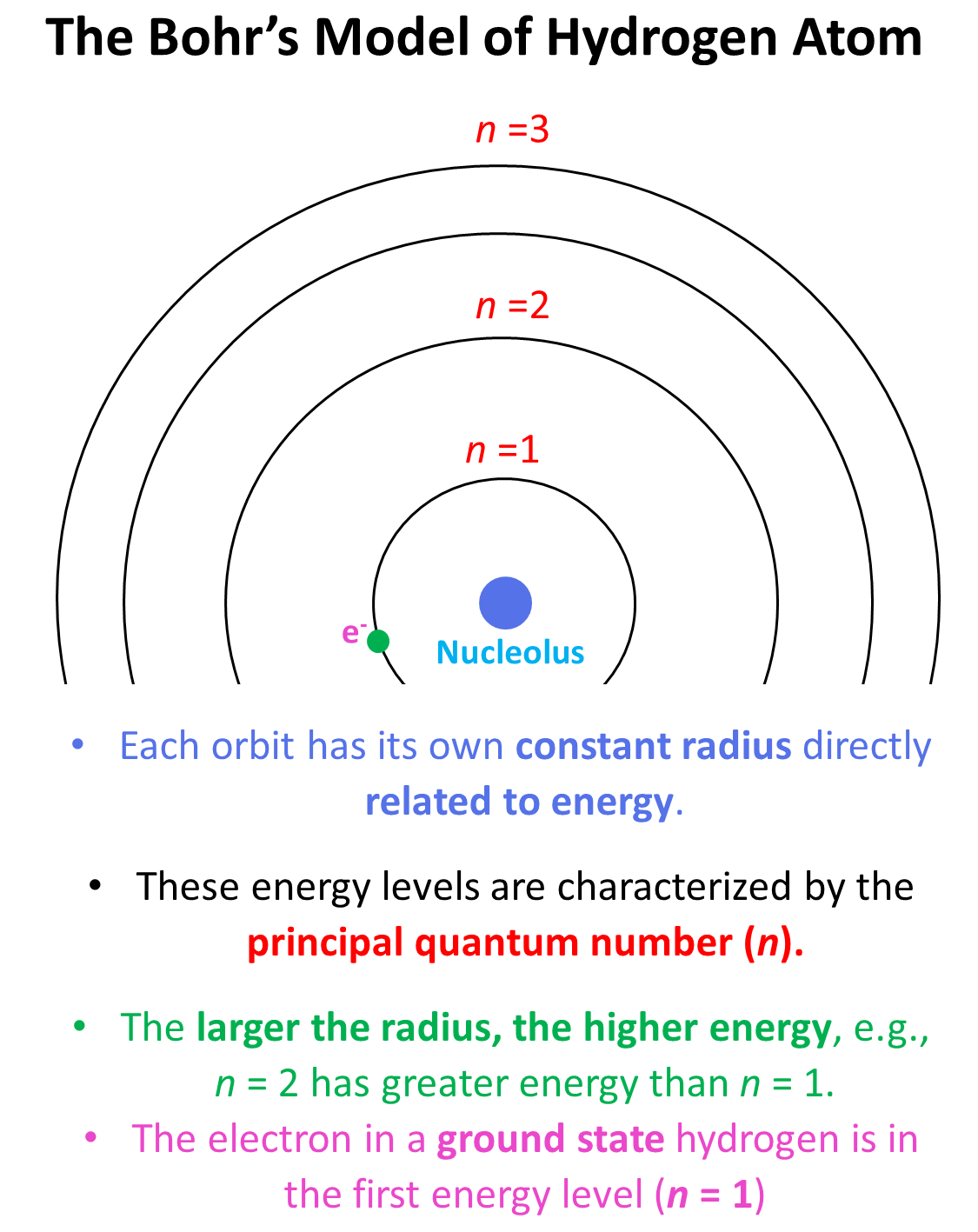
Generally, when the electron(s) is in the lowest possible energy level, the atom is said to be in the ground state, and when it is in a higher energy state, the atom is in an excited state. Importantly, the electron cannot randomly change orbits. To go into a higher energy level, it needs to absorb energy, and falling back into a lower energy level, it releases energy mainly in the form of light.
So, absorbing light with sufficient energy moves the electron to a higher energy level, and when it falls back to a lower energy level, light is emitted as energy is lost.
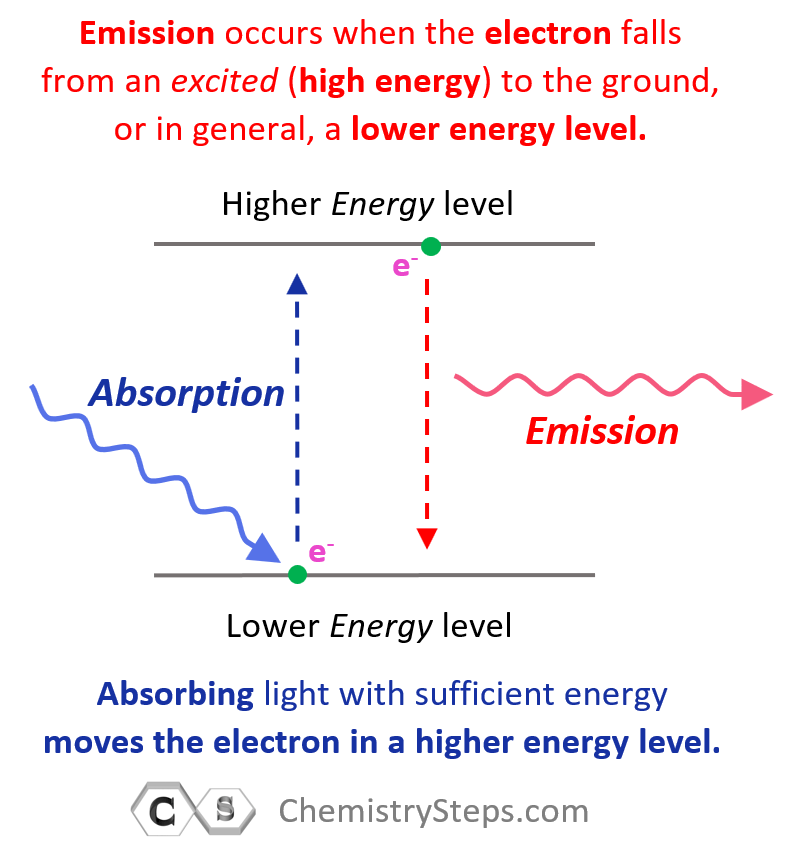
Each transition is characterized by specific (quantized) energy and therefore, the higher the energy of incident light (shorter wavelength, higher frequency), the greater the energy level the electron jumps to.
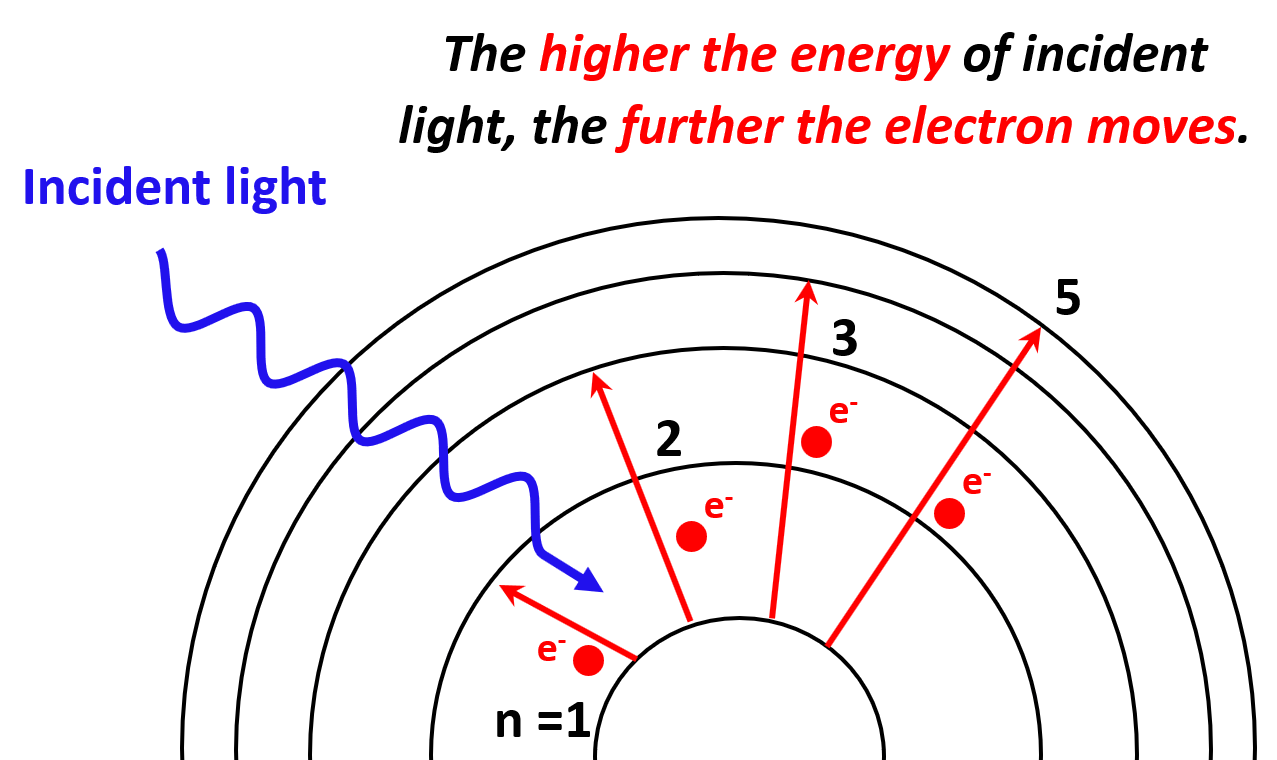
One question you may be wondering is what happens if we keep increasing the energy of the incident light? It turns out that the electron will eventually leave the atom, so let’s see how that happens.
The Photoelectric Effect
We have seen that electrons can transition to higher energy levels if sufficient energy is provided. So, what would happen if the photons striking the electrons have higher energy than the energy level of the greatest orbit? In this case, the electron is expelled from the atom as it passes through all the energy barriers associated it the orbital energy levels:

So, the next question is to figure out how much this energy should be for a given atom in order to kick out electrons from the atom. And this is what the photoelectric effect is used for.
The Photoelectric Effect
To illustrate the photoelectric effect, photons of different energies are shined on a metal surface.
If the light has high enough energy, then electrons are expelled from the metal surface, while below certain threshold, there is no ejection of electrons. For example, most metals do not demonstrate a photoelectric effect when a red light is shined on their surface because it has a relatively low energy.

On the other hand, if blue light is shined, electrons from many metals are expelled as the blue light has a higher energy and therefore, the photons are characterized with higher frequency.
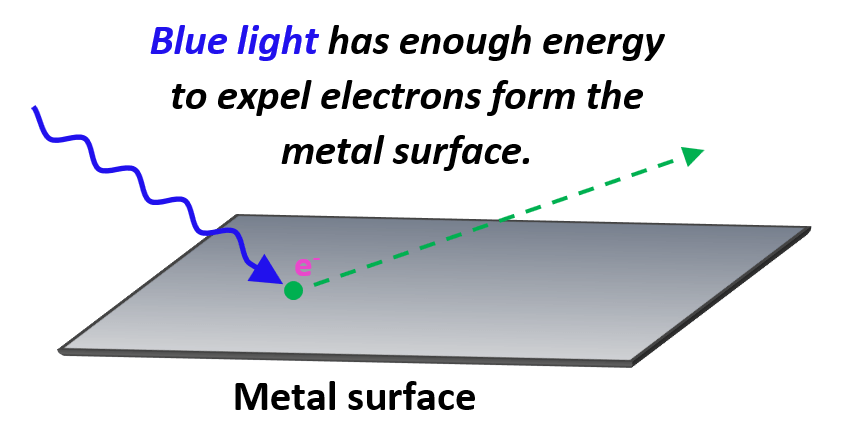
The minimum frequency of the photon required to dislodge an electron from the metal surface is called the threshold frequency.
The minimum energy required to expel an electron is called the work function (Φ) and is characteristic of each metal. These are generally the lowest for the group 1A and group 2A elements as their electrons are bound less tightly than those of other metals.
Let’s see an example. What is the minimum frequency, and the maximum wavelength of light needed to eject an electron from lithium given its function is 283 kJ/mol?
The first you need to remember is that all the formulas for energy, frequency, wavelength and etc., are for one photon, and therefore, we must express the work function is Joules instead of kJ/mol to use it in the calculations.
Let’s from now on, instead of Φ, use Eo for the work function, νo for the threshold frequency.
\[{E_{\rm{o}}}\;{\rm{ = }}\;\frac{{{\rm{283}}\,\cancel{{{\rm{kJ}}}}}}{{\cancel{{{\rm{mol}}}}}}\;{\rm{ \times }}\,\frac{{{\rm{1000}}\,{\rm{J}}}}{{{\rm{1}}\;\cancel{{{\rm{kJ}}}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;\cancel{{{\rm{mol}}}}}}{{{\rm{6}}{\rm{.02}}\,{\rm{ \times }}\;{\rm{1}}{{\rm{0}}^{{\rm{23}}}}\,\cancel{{{\rm{photon}}}}}}\;{\rm{ = }}\,{\rm{4}}{\rm{.70}}\;{\rm{ \times }}\;{\rm{1}}{{\rm{0}}^{{\rm{ – 19}}}}\,{\rm{J/photon}}\]
After this, all we need to do is rearrange the formula for energy, Eo = hνo to find the frequency:
\[{\nu _o}\, = \,\frac{{{E_{\rm{o}}}}}{h}\;{\rm{ = }}\;\frac{{{\rm{4}}{\rm{.70}}\;{\rm{ \times }}\;{\rm{1}}{{\rm{0}}^{{\rm{ – 19}}}}\,\cancel{{\rm{J}}}}}{{{\rm{6}}{\rm{.626}}\,{\rm{ \times }}\;{\rm{1}}{{\rm{0}}^{{\rm{ – 19}}}}\,\cancel{{\rm{J}}}\, \cdot \,s}}\;{\rm{ = }}\,{\rm{7}}{\rm{.90}}\;{\rm{ \times }}\;{\rm{1}}{{\rm{0}}^{{\rm{14}}}}\,{{\rm{s}}^{{\rm{ – 1}}}}\,{\rm{ = }}\,{\rm{7}}{\rm{.90}}\;{\rm{ \times }}\;{\rm{1}}{{\rm{0}}^{{\rm{14}}}}\,{\rm{Hz}}\]
For the next question, we use the correlation between frequency and wavelength to find the maximum wavelength of the light capable of expelling an electron from lithium.
\[\lambda \;{\rm{ = }}\;\frac{c}{\upsilon }\; = \;\frac{{{\rm{3}}\,{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{\rm{8}}}\,{\rm{m/}}\cancel{{\rm{s}}}}}{{{\rm{7}}{\rm{.90}}\;{\rm{ \times }}\;{\rm{1}}{{\rm{0}}^{{\rm{14}}}}\,\cancel{{{{\rm{s}}^{{\rm{ – 1}}}}}}\;}}\, = \,3.80\,{\rm{ \times }}\;{\rm{1}}{{\rm{0}}^{{\rm{ – 7}}}}\,{\rm{m}}\]
And since the wavelength is normally given in nanometers, we can also do the following conversion:
\[\lambda \; = \,3.80\; \times \;{10^{ – 7}}\,\cancel{{\rm{m}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}{{\rm{0}}^{\rm{9}}}\;{\rm{nm}}}}{{{\rm{1}}\;\cancel{{\rm{m}}}}}\; = \;380.\;{\rm{nm}}\]
Let’s now consider what will happen if we keep increasing the energy of incident light. You can think of it this way: the stronger the photon with sufficient energy kicks the electron, the faster the latter is going to be ejected. Some of the energy is consumed to dislodge the electron and the rest of it transforms into the kinetic energy of the electron. So, we can write the following equation correlating the energy of the photon with the work function of the metal and the kinetic energy of the electron:
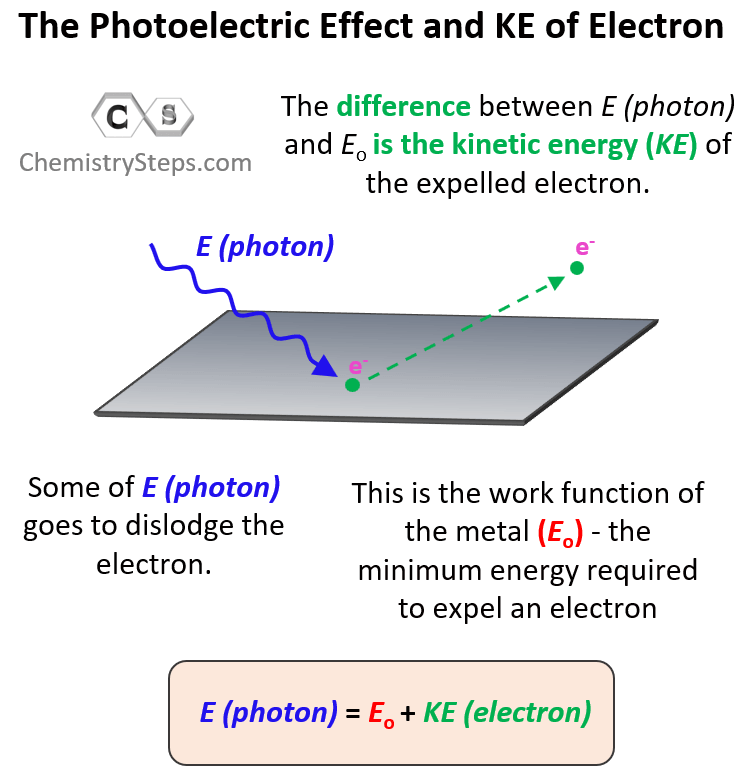
The incident light is powerful enough to dislodge the electron and expelled with certain kinetic energy. Therefore, it is the sum of the work function of the metal and the kinetic energy of the electron.
Now, sometimes, you may be asked to calculate the kinetic energy or the velocity of the electron. The kinetic energy (KE) of the ejected electron is the difference between the energy of the photon and the work function of the metal (the binding energy of the electron). So, to calculate it, you will need to rearrange this equation as:
KE = E (photon) – Eo
For example, it takes 208.4 kJ of energy to remove 1 mole of electrons from the surface of a metal. What would be the kinetic energy and the velocity of an electron ejected when a light of 416 nm is shined on this metal?
(Kinetic energy)
Let’s first check what we are missing to calculate the kinetic energy using the KE = E (photon) – Eo formula. The energy of photons can be calculated using the formula E = hc/λ which we all have. Once we find this, we can subtract from it the work function (Eo) to determine the kinetic energy of the electron.
Once again, remember to convert the energy to Joules per photon or simply Joules.
\[{E_{\rm{o}}}\;{\rm{ = }}\;\frac{{208.4\,\cancel{{{\rm{kJ}}}}}}{{\cancel{{{\rm{mol}}}}}}\;{\rm{ \times }}\,\frac{{{\rm{1000}}\,{\rm{J}}}}{{{\rm{1}}\;\cancel{{{\rm{kJ}}}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;\cancel{{{\rm{mol}}}}}}{{{\rm{6}}{\rm{.02}}\,{\rm{ \times }}\;{\rm{1}}{{\rm{0}}^{{\rm{23}}}}\,\cancel{{{\rm{photon}}}}}}\;{\rm{ = }}\,{\rm{3}}{\rm{.4618}}\;{\rm{ \times }}\;{\rm{1}}{{\rm{0}}^{{\rm{ – 19}}}}\,{\rm{J/photon}}\]
This is the energy required to dislodge one electron from the metal, and we will round off the significant figures in the end.
Let’s convert the wavelength to meters as the speed of light (c) is equal to 108 m/s.
\[\lambda \;{\rm{ = }}\,{\rm{416}}\,\cancel{{{\rm{nm}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\;{\rm{m}}}}{{{\rm{1}}{{\rm{0}}^{\rm{9}}}\;\cancel{{{\rm{nm}}}}}}\;{\rm{ = }}\;{\rm{4}}{\rm{.16}}\,{\rm{ \times }}\,{10^{ – 7}}\;{\rm{m}}\]
Now we can calculate the energy of one photon for the 416 nm light.
\[E\; = \;\frac{{hc}}{\lambda }\; = \;\frac{{\left( {{\rm{6}}{\rm{.626}}\; \times \;{{10}^{ – 34}}\;{\rm{J}} \cdot \cancel{{\rm{s}}}} \right)\,\left( {3\; \times \,{{10}^8}\,\cancel{{\rm{m}}}{\rm{/}}\cancel{{\rm{s}}}} \right)}}{{{\rm{4}}{\rm{.16}}\,{\rm{ \times }}\,{{10}^{ – 7}}\;\cancel{{\rm{m}}}}}\; = \;4.7783\, \times \;{10^{ – 19}}\,{\rm{J}}\]
So, 4.7783 x 10-19 J energy is brought by the photon, and 3.4618 x 10-19 J of it goes for removing the electron. The remaining energy is transferred to the electron in the form of kinetic energy and therefore, we can calculate it by finding the difference in these energies:
KE = E (photon) – Eo
KE = 4.7783 x 10-19 J – 3.4618 x 10-19 J = 1.32 x 10-19 J
(Electron velocity)
To calculate the velocity of the electron, we need to use the formula of kinetic energy:
\[KE\;{\rm{ = }}\;\frac{1}{2}m{v^2}\,\]
Where m is the mass, and v is the velocity (of the electron)
Therefore,
\[\frac{1}{2}m{v^2}\, = \,1.32\, \times \;{10^{ – 19}}\,{\rm{J}}\,\]
Remember, 1 J = kg · m2/s2, and the mass of electron is 9.11 x 10-31 kg.
\[\frac{1}{2}m{v^2}\, = \,1.32\, \times \;{10^{ – 19}}\,{\rm{kg \cdot }}{{\rm{m}}^{\rm{2}}}{\rm{/}}{{\rm{s}}^{\rm{2}}}\,\]
\[{v^2}\, = \,\frac{{{\rm{2}}\;{\rm{ \times 1}}{\rm{.32}}\,{\rm{ \times }}\;{\rm{1}}{{\rm{0}}^{{\rm{ – 19}}}}\,{\rm{kg \cdot }}{{\rm{m}}^{\rm{2}}}{\rm{/}}{{\rm{s}}^{\rm{2}}}\,\;}}{{{\rm{mass}}}}\]
\[v\, = \,\sqrt {\frac{{{\rm{2}}\;{\rm{ \times 1}}{\rm{.32}}\,{\rm{ \times }}\;{\rm{1}}{{\rm{0}}^{{\rm{ – 19}}}}\,\cancel{{{\rm{kg}}}}{\rm{ \cdot }}{{\rm{m}}^{\rm{2}}}{\rm{/}}{{\rm{s}}^{\rm{2}}}\,\;}}{{{\rm{9}}{\rm{.11}}\,{\rm{ \times }}\;{\rm{1}}{{\rm{0}}^{{\rm{ – 31}}}}\;\cancel{{{\rm{kg}}}}}}} \]
v = 5.38 x 105 m/s
The Photoelectric Effect and Light Intensity
One more thing I wanted to address is the term “photoelectric effect” itself. What is the “electric” doing there? Well, to observe and prove the ejection of electrons, the metal plate is placed against another one which serves as a detector. They are connected to the ends of a voltmeter, and the only way a current can occur is when there is a beak of electrons going from one metal to the other.
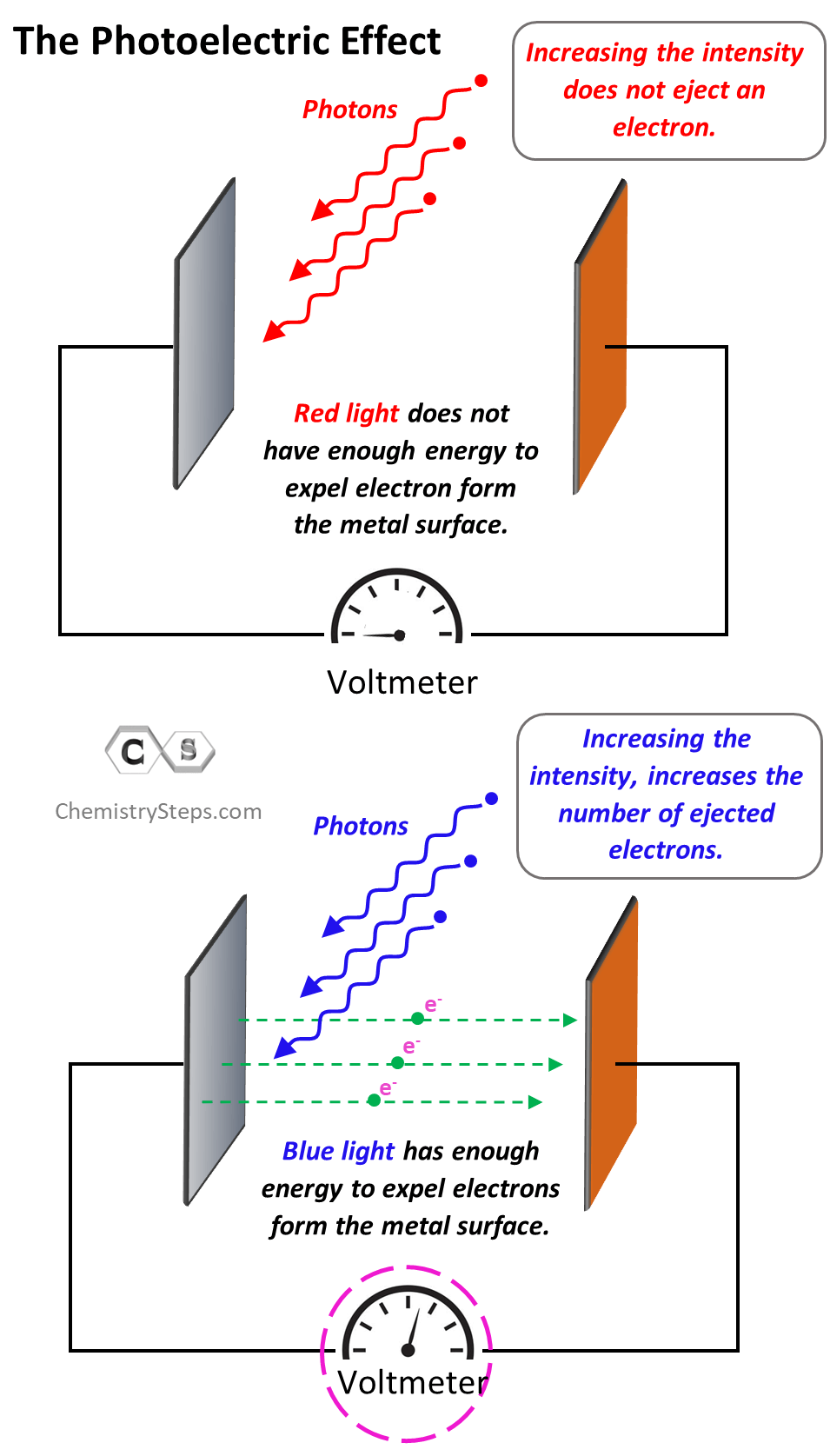
The photoelectric effect is only observed when the incident light has a certain minimum energy. If it does not, then increasing the intensity of the light won’t expel electrons. Remember, the intensity of light depends on the number of photons but not the energy of an individual photon. So, if an individual photon does not have enough energy to dislodge an electron, it wouldn’t matter how many there are in the beam of the beam. On the other hand, increasing the intensity of the light with higher energy than the work function of the metal increases the number of electrons expelled from the metal. This proves the dual nature of light and Einstein suggested that light can be viewed as a wave and small particles called photons.
Check this 95-question, Multiple-Choice Quiz on the Electronic Structure of Atoms including questions on properties of light such as wavelength, frequency, energy, quantum numbers, atomic orbitals, electron configurations, and more.
Check Also
- Atomic Orbitals
- Electron Configurations
- Electron Configurations of Ions
- Orbital Diagrams
- Aufbau’s Principle, Hund’s Rule, and Pauli’s Exclusion Principle
- Hund’s Rule
- Pauli Exclusion Principle
- Quantum Numbers (n, l, ml, ms)
- Bohr Model of the Hydrogen Atom
- Rydberg Formula
- Calculating The Energy of a Photon
- Ionization Energy
- Electron Affinity
- Energy, Wavelength, and Frequency Practice Problems

