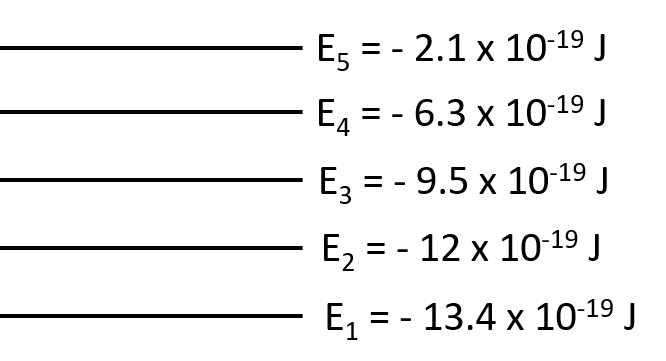Energy Frequency Wavelength and Planck’s Constant formula

General Chemistry

The energy of a photon, which is the energy of the light, can be calculated using the following two formulas:

 

 

The second formula is derived from the first by using the relationship between the frequency (ν), wavelength (λ), and speed of light (c) Plank’s constant:

 

\[\upsilon \;{\rm{ = }}\;\frac{c}{\lambda }\]

 

Before going over some examples, remember the following features of the energy, wavelength, and frequency of light:

 

 

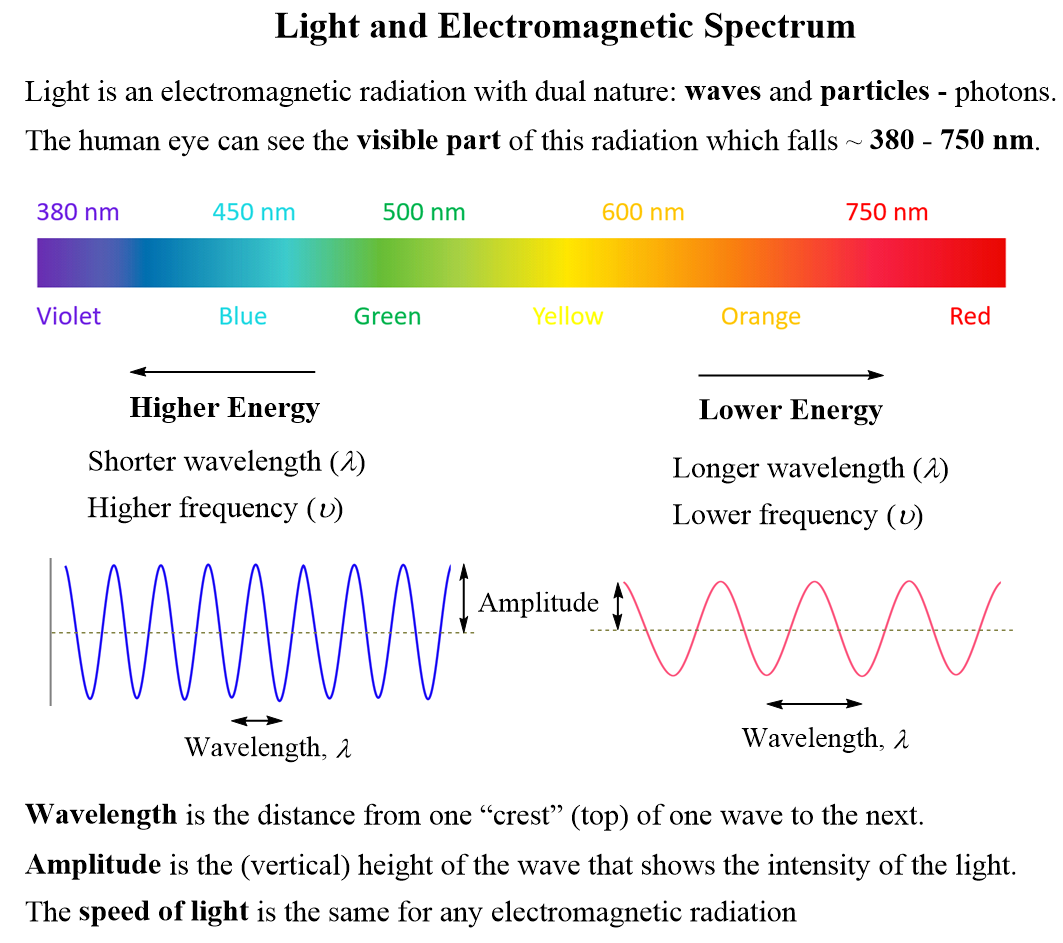
Some key correlations about the parameters of light: Higher energy means shorter wavelength (λ) and higher frequency (ν), and lower energy indicates longer wavelength (λ) and lower frequency (ν).

 

Calculating the Energy of One Photon

Example: A photon has a wavelength of 462 nm. Calculate the energy of the photon in joules. 

Solution: Frequency (ν) is inversely proportional to the wavelength (λ) and they are correlated by the following formula:

E = hν

\[\upsilon \;{\rm{ = }}\;\frac{c}{\lambda }\]

 

Therefore, we can substitute the frequency (ν) with this expression and get a new formula correlating the energy and the wavelength:

                                                                                          

\[E\; = h\upsilon \; = \;\frac{{hc}}{\lambda }\]

 

Always make sure all the units in the formula match! In this case, we need to match the units of wavelength to those of c (speed of light) which is 3 x 108 m/s, and because 1 nm = 10-9 m, we add the 10-9 exponent in the denominator.

 

\[E\; = \;\frac{{hc}}{\lambda }\; = \;\frac{{\left( {{\rm{6}}{\rm{.626}}\; \times \;{{10}^{ – 34}}\;{\rm{J}} \cdot \cancel{{\rm{s}}}} \right)\,\left( {3\; \times \,{{10}^8}\,\cancel{{\rm{m}}}{\rm{/}}\cancel{{\rm{s}}}} \right)}}{{462\, \times \,{{10}^{ – 9}}\;\cancel{{\rm{m}}}}}\; = \;4.30\, \times \;{10^{ – 19}}\,{\rm{J}}\]

 

Note: This is the energy of one photon and can also be written as 4.30 x 10-19 J/photon.

 

Calculating the Energy Based on the Moles of Photons

Example: What is the energy of 1 mol of photons, in kJ, for a 724 nm red light?

Solution: Remember, the formula correlating the energy and the wavelength is for one photon. Therefore, we can calculate the energy of one photon for the light of 724 nm wavelength. Once we find this, we can multiply the value by Avogadro’s number to determine the energy of one mole of photons. 

 

So, first, let’s calculate the energy of one photon:

 

\[E\; = \;\frac{{hc}}{\lambda }\; = \;\frac{{\left( {{\rm{6}}{\rm{.626}}\; \times \;{{10}^{ – 34}}\;{\rm{J}} \cdot \cancel{{\rm{s}}}} \right)\,\left( {3\; \times \,{{10}^8}\,\cancel{{\rm{m}}}{\rm{/}}\cancel{{\rm{s}}}} \right)}}{{724\, \times \,{{10}^{ – 9}}\;\cancel{{\rm{m}}}}}\; = \;2.7\underline 4 558\, \times \;{10^{ – 19}}\,{\rm{J/photon}}\]

 

The underlined number is to keep track of three significant figures which we will round off the final answer to.

Now, because one mole contains 6.02 x 1023 photons, we need to multiply the energy of one photon by Avogadro’s number:

 

\[E\; = \;2.7\underline 4 558\,{\rm{ \times }}\;{\rm{1}}{{\rm{0}}^{{\rm{ – 19}}}}\,\frac{{\rm{J}}}{{\cancel{{{\rm{photon}}}}}}\;{\rm{ \times }}\;\frac{{{\rm{6}}{\rm{.02}}\,{\rm{ \times }}\;{\rm{1}}{{\rm{0}}^{{\rm{23}}}}\,\cancel{{{\rm{photon}}}}}}{{{\rm{1}}\;{\rm{mol}}}}\;{\rm{ = }}\,{\rm{165,284}}\,{\rm{J/mol}}\;{\rm{ = }}\;{\rm{165}}\;{\rm{kJ/mol}}\]

 

Calculating the Number of Photons

Example: Calculate the number of photons in a laser pulse with a wavelength of 537 nm that contains 6.29 mJ (milli Joules) of energy.

Solution: Remember, the formula correlating the energy and the wavelength is for one photon. Therefore, we can calculate the energy of one photon for the light of 537 nm wavelength. Once we find this, we can compare it with 6.29 mJ to determine how many photons would make that much energy.

So, first, let’s calculate the energy of one photon:

 

\[E\; = \;\frac{{hc}}{\lambda }\; = \;\frac{{\left( {{\rm{6}}{\rm{.626}}\; \times \;{{10}^{ – 34}}\;{\rm{J}} \cdot \cancel{{\rm{s}}}} \right)\,\left( {3\; \times \,{{10}^8}\,\cancel{{\rm{m}}}{\rm{/}}\cancel{{\rm{s}}}} \right)}}{{537\, \times \,{{10}^{ – 9}}\;\cancel{{\rm{m}}}}}\; = \;3.7\underline 0 167\, \times \;{10^{ – 19}}\,{\rm{J/photon}}\]

 

Next, we need to match the units of energy. We can convert the J to mJ (1 J = 1000 mJ).

                                               

\[E\; = \;3.7\underline 0 167\;{\rm{ \times }}\;{\rm{1}}{{\rm{0}}^{{\rm{ – 19}}}}\,\cancel{{\rm{J}}}\,{\rm{ \times }}\;\frac{{{\rm{1000}}\;{\rm{mJ}}}}{{{\rm{1}}\;\cancel{{\rm{J}}}}}\, = \;3.7\underline 0 167\;{\rm{ \times }}\;{\rm{1}}{{\rm{0}}^{{\rm{ – 16}}}}\;{\rm{mJ}}\]

 

And now, we use this energy as a conversion factor to determine the number of photons:

                                

\[{\rm{N(photons)}}\;{\rm{ = }}\,\;\frac{{{\rm{1}}\,{\rm{photon}}}}{{3.7\underline 0 167\;{\rm{ \times }}\;{\rm{1}}{{\rm{0}}^{{\rm{ – 16}}}}\;\cancel{{{\rm{mJ}}}}}}\;{\rm{ \times }}\,6.29\,\cancel{{{\rm{mJ}}}}\;{\rm{ = }}\;1.70\, \times \;{10^{16}}\;{\rm{photons}}\]

 

Alternatively, you can set up a cross-multiplication correlation for the energy and the number of photons:

 

1 photon – 3.701675 x 10-16 mJ

x photons – 6.29 mJ

 

Cross multiplying x with 3.701675 x 10-16 mJ, and 1 with 6.29 mJ, we can find the x:

                                                    

\[{\rm{x}}\; = \;\frac{{{\rm{1}}\;{\rm{photon}}\;{\rm{ \times }}\;{\rm{6}}{\rm{.29}}\,\cancel{{{\rm{mJ}}}}}}{{3.701675\;{\rm{ \times }}\;{\rm{1}}{{\rm{0}}^{{\rm{ – 16}}}}\;\cancel{{{\rm{mJ}}}}}}\;{\rm{ = }}\;{\rm{1}}{\rm{.70}}\,{\rm{ \times }}\;{\rm{1}}{{\rm{0}}^{{\rm{16}}}}\;{\rm{photons}}\]

 

Check this 95-question, Multiple-Choice Quiz on the Electronic Structure of Atoms including questions on properties of light such as wavelength, frequency, energy, quantum numbers, atomic orbitals, electron configurations, and more. 

 

Check Also

 

Practice

Join Chem Steps today to access all the Practice Problems together with Quizzes and Study guides.
1.

Calculate the frequency of the light with a wavelength of 756 nm.

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
2.

A photon has a wavelength of 587 nm. Calculate the energy of the photon in joules.

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
3.

An FM station broadcasts music at a radio wave with a frequency of 115 MHz. Calculate the wavelength of these radio waves.

 

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
4.

The blue light used in dental curing has a frequency of about 7.2 x 1014 Hz. What is the wavelength, in nm, associated with this radiation?

 

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
5.

Calculate the number of photons in a laser pulse with a wavelength of 624 nm that contains 4.19 mJ of energy.

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
6.

What is the energy of 1 mol of photons, in kJ, for a 520. nm green light?

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
7.

The ultraviolet (UV) light is dangerous to human beings. Calculate the energy of a single UV photon and a mole of UV photons with a wavelength of 165 nm.

 

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
8.

The UV light associated with sunburn symptoms has an energy of about 400. kJ/mole. Which of the following compounds would be suitable to use in a sunscreen to protect from UV radiation?

A – 450 nm, B – absorbs 560 nm, C – absorbs 300 nm, C – absorbs 120 nm

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
9.

How many moles of a metal are in a sample that emits light at a wavelength of 345 nm if the total energy is 2.54 x 105 J. Assume that each atom emits one photon.

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
10.

Certain cancer cells are killed by photodynamic therapy by radiating a light in the range of wavelengths from 650 to 1350 (nm). This is called the biological or therapeutic window. Which of the following lasers could be used for this purpose?

 

 

Laser A – emits light of 4.00 x 108 MHz

Laser B – emits light of 5.40 x 108 MHz

Laser C – emits light of 6.62 x 108 MHz

a)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
11.

In the coming up semesters you might be taking organic chemistry where infrared (IR) spectroscopy is used to determine the functional groups in the molecule. The principle of IR spectroscopy is that each type of covalent bond absorbs a specific range of radiation in the IR region that matches the vibration of the atoms in the bond. For example, the C-C bond absorbs the light of 3.44 μM. What is the vibrational frequency of the C-C bond in Hz?

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
12.

Rank the following electromagnetic waves in order of (a) increasing energy; (b) increasing frequency; (c) increasing amplitude.

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
13.

Answer the questions below for the following representation of an electromagnetic radiation:

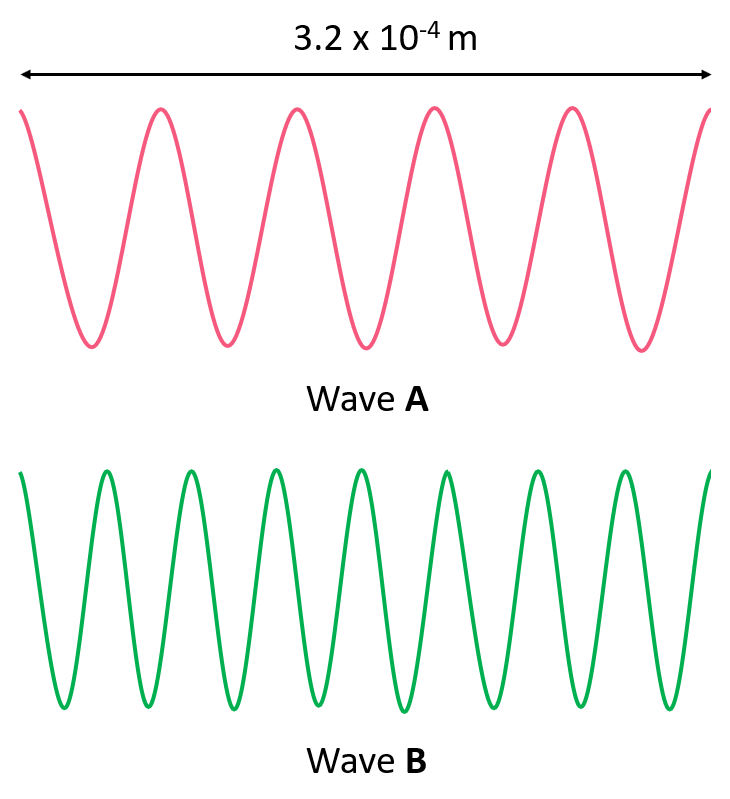
a) Calculate the wavelength of each radiation.

b) Which wave has the higher energy?

c) Which wave has the higher frequency?

d) Which wave has the greater velocity?

e) Calculate the energy and frequency of each wave.

 

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
14.

The energy required to remove an electron from an aluminum atom is 6.73 x 10-22 kJ. Calculate the maximum wavelength, in nm, of light that can do this.

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
15.

The energy required to expel an electron from an atom in gas phase is called ionization energy. Would a light beam of 256 nm be enough to ionize a silver atom given that its ionization energy is 731 kJ/mol?

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
16.

Calculate the velocities of electrons with de Broglie wavelengths of 285 nm.

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
17.

Calculate the de Broglie wavelength of an electron traveling at 5.47 x 104 m/s.

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
18.

Hydrogen Atom: The Bohr Model

1Some electron transitions are shown below on a Bohr-model representation of the H atom.

 

 

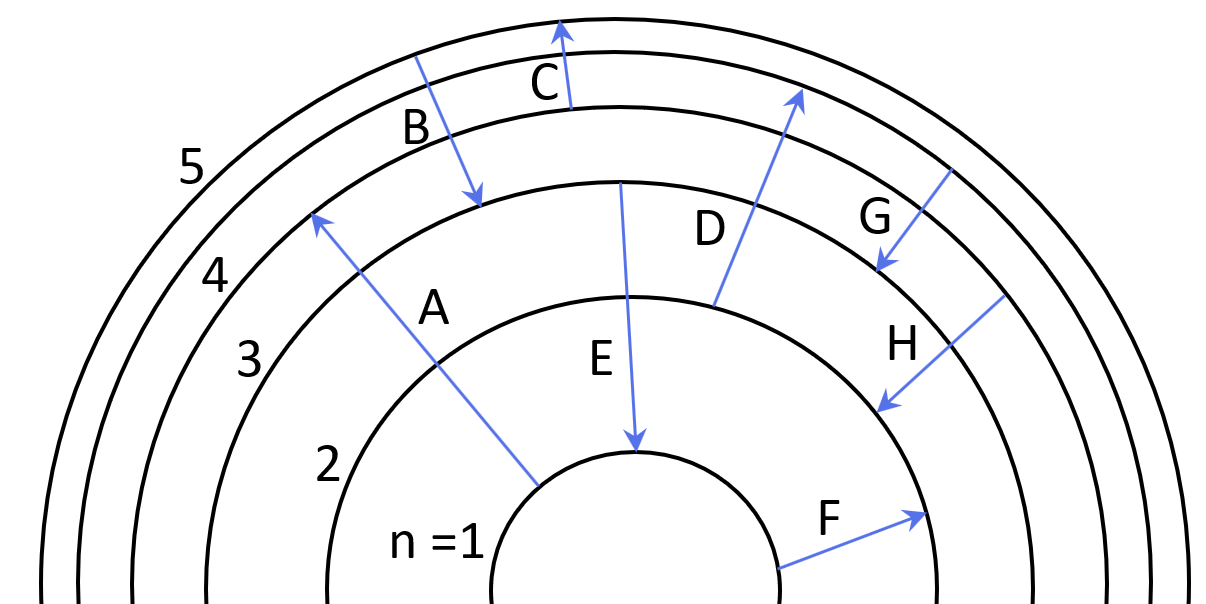
(a) Classify each transition as absorption or emission.

(b) Arrange the absorptions in terms of increasing energy.

(c) Rank the emissions in terms of decreasing wavelength of light.

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
19.

For each of the following transitions, use the Rydberg equation to calculate the wavelength of light emitted by a hydrogen atom:

a) n = 3 → n = 2

b) n = 4 → n = 1

c) n = 6 → n = 3

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
20.

What is the maximum wavelength of a photon that can excite the electron from n = 1 to n = 3 level in a hydrogen atom?

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
21.

What is the energy level that the electron moves when a hydrogen atom at ground state absorbs a photon of wavelength 95 nm?

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
22.

Would a photon of 115 nm light have sufficient energy to excite an electron in a ground state hydrogen atom to the n = 4 energy state?

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
23.

What is the wavelength of the photon needed to excite an electron from the E1 to E4 level for a hypothetical atom given the following energy levels:

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the Answers and Solutions for all the Practice Problems, Quizzes, and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  

Leave a Comment