In the previous post, we talked about significant figures, the ways of counting them, and their importance in the certainty of measurements. Significant figures of a measured number also dictate the certainty of the answer obtained by mathematical operations such as addition, subtraction, multiplication, and division. The idea behind this is that we cannot have an answer that is more certain than the starting numbers because the calculations are based on those initial measurements with their certainty. Therefore, there are rules we need to be familiar with when doing calculations involving measured numbers. There are two main rules applied to addition and subtraction and multiplication and division respectively.

Significant Figures in Multiplication and Division
In multiplication or division, the answer can’t have more significant figures than either of the original numbers. More specifically, the answer should have the same number of significant figures as the one with the fewest significant figures.

If you checked the calculation with a calculator, you would see that the answers have more digits and this is where we are limited to not having as many numbers as we see. Recall the rules for rounding off to the correct number of significant figures. The number is rounded down if the one to the right is four or less, and we round up if the next digit is five or more.
For example, in the multiplication above the exact answer is 17.75845, however, we round it to 3 significant figures according to the number 8.65 which has three significant figures, while 2.053 has four significant figures. This means the 17.75845 needs to be rounded up because of the 5 next to it:

Same for the division, 138 ÷ 11.9 = 11.596638, and we round up the 5 to 6 because of the 9 on the right. Therefore, the answer is 11.6.

Significant Figures in Addition and Subtraction
When doing addition or subtraction, the answer carries the same number of decimal places as the number with the fewest decimal places. Don’t forget to apply the same rules for rounding off as well.

Now, here is an interesting question:
What if one or all the numbers do not have decimal places?
How do we determine the correct number of significant figures in an addition or subtraction when there is no decimal place?
Remember, the whole idea of rounding off is to drop the insignificant digits. These are all the digits to the right of the last significant digit.
For example, what is the answer to 23 – 14.6? 23 does not have a decimal place, which means the 3 is the last significant figure, and all the digits after it should be dropped following the rules for rounding off.
The calculator gives 8.4, however, we round it to 8 with no decimal place because the number with the least number of decimal places (23) has none.
You can still do this by drawing a line like we did for numbers with decimal places. In this case, the line stops at the 1 because it is the last significant figure:

In other words, we can say that we rounded the answer to the ones place because 23 has the certainty of ones which is less than tenths (8.4).
Let’s look at another example: 5,289 + 100?
The sum of 5,289 and 100 is 5,389 but we need to round the final answer. The first number (5,289) ends with the ones place, while the second number (100) is significant only to the hundreds place, and therefore, we round 5,389 to the hundreds place: 5,400 (no decimal at the end).
Drawing a line is still a good approach to follow this. Just make sure to place the numbers in correct positions (thousands, hundreds, tens etc.).

Once again, remember that these rules are only for measured numbers. For example, adding the number of students in a class of 300 and 68 does not require rounding off because these numbers are exact with an infinite number of significant figures as they are not measured with an instrument.
On the contrary, if the length of an object is measured using a ruler with a 100s grid, we cannot know the ones of this measurement; we cannot say if it is 345 or 359, but we can tell whether it is 300 or 400. So, the certainty is only applicable to the hundreds and we cannot have tens or ones in the answer when doing a mathematical operation.
Significant Numbers in Multistep Calculations
If there are more than two numbers involved in the calculation, the rule is to not round off any intermediate result and only do it for the final answer.
For example:

The calculation involves only multiplication and therefore, we keep all the digits for the intermediate numbers and round off the final answer according to the number with the fewest number of significant figures.
Now, what we mean by an intermediate result is, for example, when we multiply 3.54 by 2.6458, the answer is 9.366132. Do not round off this number to 3 significant figures yet. If we do, the answer would be 9.37 and after multiplying it by 7.48764, we get 70.159186 which, after rounding off again, gives 70.2 as a final answer.
The same would be true if there was a division in the calculation. For example,
2.1 x 5.687 ÷ 1.654 = 7.2205 ≈ 7.2
The answer has 2 significant figures based on the number 2.1.
Multistep Calculations with Mixed Operations
Let’s now discuss the significant figures when the calculation involves both subtraction division and addition subtraction. Although the same principle of rounding off only at the very end is applicable, there are some nuances we need to consider.
For example, the following calculation involves multiplication and subtraction.
4.647 x 2.5149 x (6.2594 – 2.34)
Now, the first thing is to follow the correct order of operations. Remember, the one in the parenthesis must be done before the result is multiplied by the other number. So, in this case, we first subtract 2.34 from 6.2594. The result is 3.9194 and if it was the final answer, we’d round it off to 3.92 because 2.34 has only two decimal places.
Instead, we only underline the last digit (1) to keep track of the significant figure. By the last digit, we mean the last digit that is supposed to be there based on the decimal places. Underlining the 1 indicates that the answer should have 3 significant figures after the multiplication:

Let’s do one more example of a calculation involving addition/subtraction and multiplication/division.
Calculate the answer of this calculation expressed in correct number of significant figures:
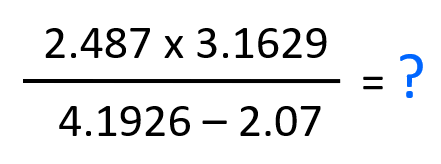
In this case, it does not matter if we do the operation in the numerator or denominator first. Let’s do the subtraction and see how many significant figures is the result going to have when we divide the product in the denominator.

The intermediate number in the denominator is limited to two decimal places which, in this case, is equivalent to three significant figures. We do not round off this number because there is still one step it is going to be used in. However, we keep in mind that it will be used as having three significant figures and because the two numbers in the numerator have more significant figures, the final answer is rounded to three significant figures.
Significant Figures in Calculations with Scientific Notation
Let’s quickly recap what scientific notation is and why we use it. We often work with extremely large or small numbers in chemistry which can be written or understood wrongly if one zero is misplaced. To avoid these mistakes and represented the numbers easier, the scientific notation is used which has a general form of N × 10n
N here is a number between 1 and 10 and n is the exponent that can be a positive or negative integer (whole number).
For example, 1.34 x 105 = 134,000, 8.6 x 10-4 = 0.00086.
For counting the number of significant figures in scientific notation, we focus on the N, which is the number that comes before the 10n. The exponent is only to tell us about the magnitude of the number.
Therefore, 1.34 x 105 has 3 significant figures, and 8.6 x 10-4 has 2 significant figures. 1.34 x 105 written as 134,000 has 6 digits and if we wanted to express 1.34 x 105 with 6 significant figures, we need to add the zeros after the decimal point in the initial number: 1.34000 x 105.
On the other hand, if the number has more digits than it is supposed to have, the initial number is rounded off according to how many significant figures there should be. For example, how can we express 46897 in two significant figures?
What we do in this case is round up the 6 to seven as there is an 8 after it, and add the corresponding exponent: 4.7 x 104.
Scientific Notation in Addition and Elimination
Now, let’s say we need to add two numbers expressed in scientific notation. For example,
2.65 x 103 + 6.4 x 103 = ?
The good news about this problem is that the exponents on the 10s are the same which means we can just add the numbers in front of the powers of ten and put the exponent next to the answer:
2.65 + 8.4 = 9.05 ≈ 9.1 x 103
Notice that we rounded the result to one decimal place as we learned for the addition and subtraction.
If you are confused about how we can add the numbers, think of this as an expression
2.65X + 6.4X
We can rewrite it by putting the numbers in parenthesis and the X outside of them:
(2.65 + 6.4) X
So, X and 103 are identical factors here, therefore, we can also write:
2.65 x 103 + 6.4 x 103 = (2.65 + 6.4) 103
If the exponents are not identical, then we can take both numbers out of scientific notation, do the addition or subtraction, and then put the answer back into scientific notation. For example,
9.578 x 103 – 5.326 x 102
First, take the numbers out of scientific notation: 9.578 x 103 = 9578, 5.326 x 102 = 532.6. And now, we can do the subtraction and convert the answer back to scientific notation, and round the answer to two decimal places.
9578 – 532.6 = 9,045.4
Round the decimals to the ones place and add the correct exponent according to the magnitude of the number:
9,045.4 ≈ 9,045 = 9.045 x 103
We can still draw the line after the last significant figure to make this more visual:

Another approach is to match the exponents by changing one of the numbers in front of the 10s.
For example, 3.48 x 102 – 8.46 x 101 can be written as 3.48 x 102 – 0.846 x 102.
We decrease 8.46 ten times by moving the decimal to the left and to balance this, the exponent is increased by one. After this, we can subtract the numbers and add the 102:
3.48 x 102 – 0.846 x 102 = (3.48 – 0.846) x 102 = 2.634 x 102 ≈ 2.63 x 102
Notice that we rounded the decimal place to the hundredths place based on 3.48. 0.846 has a certainty of thousandths place but we are limited to the hundredth’s place by 3.48.

Scientific Notation in Multiplication and Division
First, remember the rules for changing the exponent during multiplication and subtraction. When multiplying the exponents are added, and when divided, the exponents are subtracted.
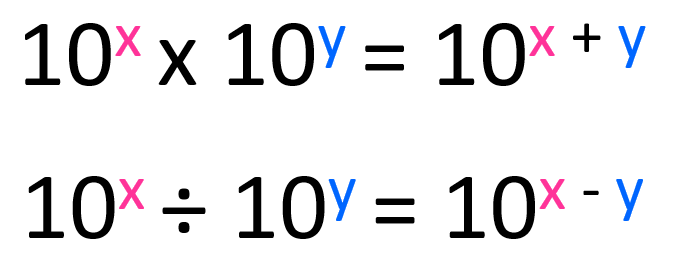
The numbers in front of the 10s are multiplied and divided accordingly.

For example, what is the answer to this calculation expressed in scientific notation?
(3.4 × 10-6) × (2.5 × 104)
We multiply the numbers in front of the × 10 (3.4 x 2.5 = 8.5), and then add the exponents from the powers of ten (10-6 × 104 = 10-6 +4 = 10-2). Therefore, the answer is 8.5 × 10-2.
Check Also
- Significant Figures
- Significant Figures Practice Problems
- Converting Units With Conversion Factors Dimensional Analysis
- Conversion Factors and Dimensional Analysis Practice Problems
- Density Practice Problems
Practice
Perform the following calculations and report the answers in the correct number of significant figures.

