In these practice problems, we will work on determining the density, volume, and the mass of different objects. First, density is calculated by the ratio of the mass and the volume of the object:
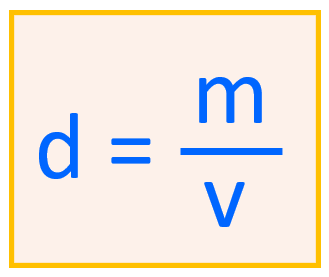
For example, what is the density of a metal if its 2.35 g sample has a volume of 0.654 g/mL?
\[{\rm{d}}\;{\rm{ = }}\,\,\frac{{\rm{m}}}{{\rm{v}}}\,{\rm{ = }}\frac{{{\rm{2}}{\rm{.35}}\,{\rm{g}}}}{{{\rm{0}}{\rm{.654}}\,{\rm{mL}}}}\,{\rm{ = }}\;{\rm{3}}{\rm{.59}}\,{\rm{g/mL}}\]
Sometimes the volume may not be given and there are two main scenarios here depending on if the object has a regular or irregular shape. So, let’s discuss them one by one.
The density of Objects with Regular Shapes
The first example here would be the density of an object with a cubic shape. For example, a wood block with a length of 11 in, 7.5 in width and 1.95 in thickness weighs 4.93 lb. Calculate density of the block in lb/in3.
The mass is given and therefore, the only thing missing is the volume of the block which we find by multiplying all the sides:
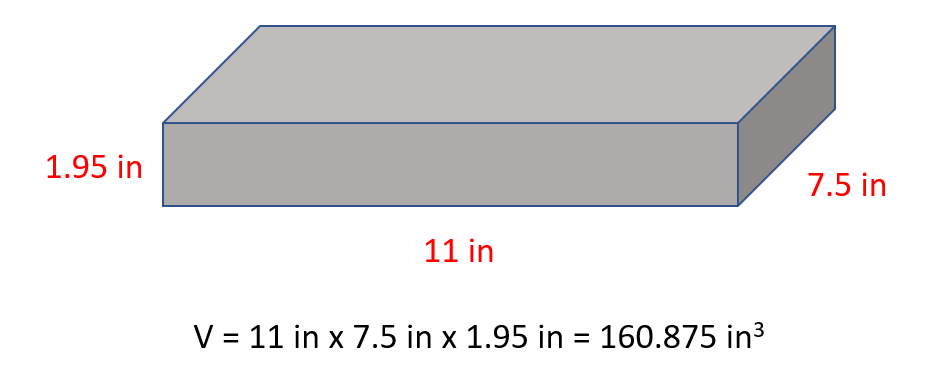
And now, we can determine the density:
\[{\rm{d}}\;{\rm{ = }}\,\,\frac{{\rm{m}}}{{\rm{v}}}\,{\rm{ = }}\frac{{{\rm{4}}{\rm{.93}}\,{\rm{lb}}}}{{{\rm{160}}{\rm{.875}}\,{\rm{i}}{{\rm{n}}^{\rm{3}}}}}\,{\rm{ = }}\;{\rm{0}}{\rm{.031}}\,{\rm{lb/i}}{{\rm{n}}^{\rm{3}}}\]
The density of Objects with Irregular Shapes
The most common example here is the one where the density of metal pellets needs to be determined. For example, a sample containing 15.4 g of metal pellets is poured into a graduated cylinder initially containing 12.0 mL of water, causing the water level in the cylinder to rise to 16.2 mL. Calculate the density of the metal.
What you need to visualize in these problems, is that the volume of pellets or anything else that was added to water, is equal to the volume of the water displaced:
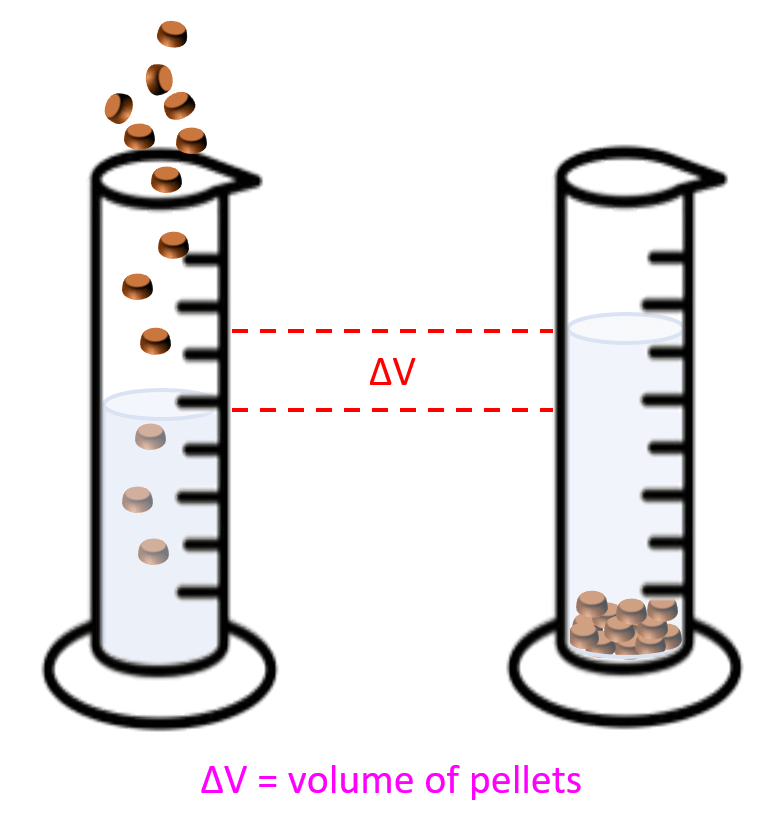
So, in this case, the volume of the pellets would be:
16.2 – 12.0 = 4.20 mL
Therefore, the density is the ratio of the mass and this difference in initial and final volumes:
\[{\rm{d}}\;{\rm{ = }}\,\,\frac{{\rm{m}}}{{\rm{v}}}\,{\rm{ = }}\frac{{{\rm{15}}{\rm{.4}}\,{\rm{g}}}}{{{\rm{4}}{\rm{.20}}\,{\rm{mL}}}}\,{\rm{ = }}\;{\rm{3}}{\rm{.67}}\,{\rm{g/mL}}\]
Density When the Units are Different
Another type of problem is when the initial units are different than what they are asked to be in the answer. For example, determine the density of a plastic in g/cm3 if a 1.39-lb piece occupies 6.48 in3 volume.
First, we can calculate the density in lb/in3 and then convert the units to g/cm3.
\[{\rm{d}}\;{\rm{ = }}\,\,\frac{{\rm{m}}}{{\rm{v}}}\,{\rm{ = }}\frac{{{\rm{1}}{\rm{.39}}\,{\rm{lb}}}}{{{\rm{6}}{\rm{.48}}\,{\rm{i}}{{\rm{n}}^{\rm{3}}}}}\,{\rm{ = }}\;{\rm{0}}{\rm{.2145}}\,{\rm{lb/i}}{{\rm{n}}^{\rm{3}}}\]
Now, remember, for converting two units, we treat them like separate units and do the conversions one by one. Check the “Multi-Step Unit Conversion” section here for more details.
\[{\rm{0}}{\rm{.2145}}\;\frac{{\cancel{{{\rm{lb}}}}}}{{\cancel{{{\rm{i}}{{\rm{n}}^{\rm{3}}}}}}}\,{\rm{ \times }}\,\frac{{{\rm{453}}{\rm{.6}}\,{\rm{g}}}}{{{\rm{1}}\;\cancel{{{\rm{lb}}}}}}\,{\rm{ \times }}\,\frac{{{\rm{(1}}\,\cancel{{{\rm{in}}{{\rm{)}}^{\rm{3}}}}}}}{{{{{\rm{(2}}{\rm{.54}}\,{\rm{cm)}}}^{\rm{3}}}}}\,{\rm{ = }}\;{\rm{5}}{\rm{.94}}\,{\rm{g/c}}{{\rm{m}}^{\rm{3}}}\,\,\]
So, in the first part, we converted pounds to grams, and the second multiplication was to convert in3 to cm3. Remember, you need to apply the exponent to both the number and the unit when converting units raised to a power (Converting Units Raised to Power).
The density of a Cylinder
Another common question is determining the density of a cylinder. What you need to remember here is the formula that may not be given:
If you forget it, try to remember the formula for the surface of circle:
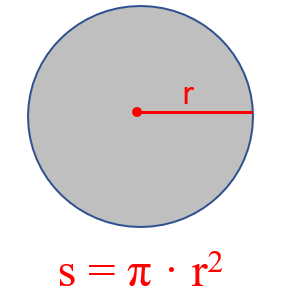
Now you can visualize the cylinder as a stack of multiple circles and therefore, its volume is the product of the circle’s surface and the height of the cylinder.
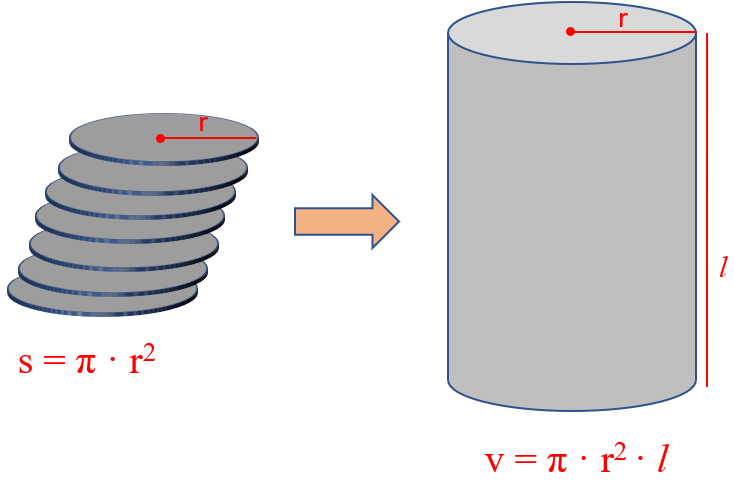
For example, a plastic cylinder has a length of 8.52 in, a radius of 2.34 in, and a mass of 5.60 lb. What is the density of the plastic in lb/in3?
The volume of a cylinder is calculated by the formula v = π · r2 · l, and therefore,
v = π · r2 · l = 3.14 x (2.34)2 in x 8.52 in = 146.488 in3
The density is the ratio of the mass and the calculated volume:
\[{\rm{d}}\;{\rm{ = }}\,\,\frac{{\rm{m}}}{{\rm{v}}}\,{\rm{ = }}\frac{{{\rm{5}}{\rm{.60}}\,{\rm{lb}}}}{{{\rm{146}}{\rm{.488}}\,{\rm{i}}{{\rm{n}}^{\rm{3}}}}}\,{\rm{ = }}\;{\rm{0}}{\rm{.0382}}\,{\rm{lb/i}}{{\rm{n}}^{\rm{3}}}\]
Mass and Volume from Density
The formula for the density can be rearranged to get an expression for the mass or the volume. For example, what is the mass of a metal block with a density of 9.25 g/ml if it occupies 14.6 cm3 volume?
Rearranging the formula for density, we ger that the mass if the product of the volume and density:
m = d x v
Therefore,
\[{\rm{m}}\;{\rm{ = }}\,{\rm{d}}\,{\rm{ \times }}\,{\rm{v}}\,{\rm{ = }}\,{\rm{9}}{\rm{.25}}\,\frac{{\rm{g}}}{{\cancel{{{\rm{mL}}}}}}\;{\rm{ \times }}\,{\rm{14}}{\rm{.6}}\,\cancel{{{\rm{mL}}}}\,{\rm{ = }}\;{\rm{135}}\;{\rm{g}}\]
Notice that 1 mL = 1cm3 that is why we replaced cm3 by ml for the volume and canceled them with the density units.
The volume is the ratio of the mass and density. For example, what is the volume of 154 g bromine in milliliters if it has a density of 3.10 g/cm3?
\[{\rm{v}}\;{\rm{ = }}\,\frac{{\rm{m}}}{{\rm{d}}}\,{\rm{ = }}\,\frac{{{\rm{154}}\,{\rm{g}}}}{{{\rm{3}}{\rm{.10}}\,{\rm{c}}{{\rm{m}}^{\rm{3}}}}}\,{\rm{ = }}\;{\rm{49}}{\rm{.7}}\,{\rm{g/c}}{{\rm{m}}^{\rm{3}}}\]
Check Also
- Significant Figures
- Significant Figures in Addition, Subtraction Multiplication, and Division
- Significant Figures Practice Problems
- Converting Units With Conversion Factors Dimensional Analysis
- Conversion Factors and Dimensional Analysis Practice Problems
Practice
How many dozen eggs are in 15,652 eggs?
1304 dozens
1 dozen = 12, therefore:
\[{\rm{15,652}}\,\cancel{{{\rm{eggs}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{dozen}}}}{{{\rm{12}}\,\cancel{{{\rm{eggs}}}}}}\;{\rm{ = }}\;1,304.3\,{\rm{dozen}}\]
How many years are in 5,489 days?
15.04 years
\[{\rm{5,489}}\,\cancel{{{\rm{days}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{year}}}}{{{\rm{365}}\,\cancel{{{\rm{days}}}}}}\;{\rm{ = }}\;{\rm{15}}{\rm{.04}}\;{\rm{years}}\]
How many weeks are in 2.5 centuries? (1 yr. = 52 weeks)
13,000 weeks
\[{\rm{2}}{\rm{.5}}\,\cancel{{{\rm{century}}}}\;{\rm{ \times }}\,\frac{{{\rm{100}}\,\cancel{{{\rm{years}}}}}}{{{\rm{1}}\,\cancel{{{\rm{century}}}}}}{\rm{ \times }}\,\frac{{{\rm{52}}\,{\rm{weaks}}}}{{{\rm{1}}\,\cancel{{{\rm{year}}}}}}{\rm{ = }}\;{\rm{13,000}}\,{\rm{weaks}}\]
Would 550 m2 of fabric be enough to upholster 200 chairs if each requires 35.4 ft2 fabric?
The material won’t be enough.
We can first determine how many ft2 of fabric is needed for 200 chairs, and then compare it to 150 m2 by convert the units of either.
200 x 35.4 ft2 = 7080 ft2
Let’s now convert this to m2 according to this plan:
\[{\rm{995}}\;{\rm{f}}{{\rm{t}}^{\rm{2}}}\;{\rm{ \times }}\,\frac{{{{{\rm{(12}}\,{\rm{in)}}}^{\rm{2}}}}}{{{{{\rm{(1}}\,{\rm{ft)}}}^{\rm{2}}}}}\,{\rm{ \times }}\,\frac{{{{{\rm{(2}}{\rm{.54}}\,{\rm{cm)}}}^{\rm{2}}}}}{{{{{\rm{(12}}\,{\rm{in)}}}^{\rm{2}}}}}\,{\rm{ \times }}\,\frac{{{{{\rm{(1}}\,{\rm{m)}}}^{\rm{2}}}}}{{{{{\rm{(100}}\,{\rm{cm)}}}^{\rm{2}}}}}\]
\[{\rm{7080}}\;\cancel{{{\rm{f}}{{\rm{t}}^{\rm{2}}}}}\;{\rm{ \times }}\,\frac{{{\rm{144}}\,\cancel{{{\rm{i}}{{\rm{n}}^{\rm{2}}}}}}}{{{\rm{1}}\,\cancel{{{\rm{f}}{{\rm{t}}^{\rm{2}}}}}}}\,{\rm{ \times }}\,\frac{{{\rm{6}}{\rm{.4516}}\,\cancel{{{\rm{c}}{{\rm{m}}^{\rm{2}}}}}}}{{{\rm{1}}\,\cancel{{{\rm{i}}{{\rm{n}}^{\rm{2}}}}}}}\,{\rm{ \times }}\,\frac{{{\rm{1}}\,{{\rm{m}}^{\rm{2}}}}}{{{\rm{10000}}\,\cancel{{{\rm{c}}{{\rm{m}}^{\rm{2}}}}}}}\, = \,658\,{{\rm{m}}^{\rm{2}}}\]
200 chairs will require 658 m2 of fabric, therefore, the material won’t be enough.
A 20.0-mL sample of a liquid has a mass of 17.8 g. What is the liquid’s density in grams per milliliter?
0.89 g/mL
\[{\rm{d}}\;{\rm{ = }}\,\,\frac{{\rm{m}}}{{\rm{v}}}\,{\rm{ = }}\frac{{{\rm{17}}{\rm{.8}}\,{\rm{g}}}}{{{\rm{20}}{\rm{.0}}\,{\rm{mL}}}}\,{\rm{ = }}\;{\rm{0}}{\rm{.89}}\,{\rm{g/mL}}\]
A sample containing 31.25 g of metal pellets is poured into a graduated cylinder initially containing 11.9 mL of water, causing the water level in the cylinder to rise to 18.7 mL. Calculate the density of the metal.
4.60 g/mL
In these types of problems, you need to realize that the volume displaced by the metal pellets is the volume of the liquid. Therefore, we have the mass and the volume of the metal, and we can calculate the density:
\[{\rm{d}}\;{\rm{ = }}\,\,\frac{{\rm{m}}}{{\rm{v}}}\,{\rm{ = }}\frac{{{\rm{31}}{\rm{.25}}\,{\rm{g}}}}{{{\rm{(18}}{\rm{.7}}\;{\rm{ – }}\,{\rm{11}}{\rm{.9)}}\;{\rm{mL}}}}\,{\rm{ = }}\;{\rm{4}}{\rm{.60}}\,{\rm{g/mL}}\]
What is the mass of a 2.85 L sample of a liquid that has a density of 0.954 g/mL?
2.72 x 103 g
The first thing is to make sure the units in density match those of volume. It is not the case here, and we can convert the L to mL first:
\[{\rm{v}}\,{\rm{ = }}\;{\rm{2}}{\rm{.85}}\,\cancel{{\rm{L}}}\; \times \,\frac{{{\rm{1000}}\,{\rm{mL}}}}{{{\rm{1}}\;\cancel{{\rm{L}}}}}\,{\rm{ = }}\;{\rm{2850}}\;{\rm{mL}}\]
And now we can calculate the mass:
\[{\rm{m}}\;{\rm{ = }}\,{\rm{d}}\,{\rm{ \times }}\,{\rm{v}}\,{\rm{ = 0}}{\rm{.954}}\,\frac{{\rm{g}}}{{\cancel{{{\rm{mL}}}}}}\;{\rm{ \times }}\,{\rm{2850}}\,\cancel{{{\rm{mL}}}}\,{\rm{ = }}\;{\rm{2}}{\rm{.72}}\;{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{\rm{3}}}\;{\rm{g}}\]
What is the volume of 100. g bromine in milliliters if it has a density of 3.10 g/cm3?
32.3 g/cm3
\[{\rm{v}}\;{\rm{ = }}\,\frac{{\rm{m}}}{{\rm{d}}}\,{\rm{ = }}\,\frac{{{\rm{100}}{\rm{.}}\,{\rm{g}}}}{{{\rm{3}}{\rm{.10}}\,{\rm{c}}{{\rm{m}}^{\rm{3}}}}}\,{\rm{ = }}\;{\rm{32}}{\rm{.3}}\,{\rm{g/c}}{{\rm{m}}^{\rm{3}}}\]
Complete the missing data for the density, mass, and volume in the following table:
| Mass | Volume | Density |
| 2.35 g | 0.035 L | X g/mL |
| X lb | 356 mL | 1.56 g/cm3 |
| 14.6 kg | X gal | 4.81 g/mL |
Row 1 – 0.0671 g/mL
Row 2 – 1.22 lb
Row 3 – 0.802 gal
For all the questions, we need to pay attention to the units.
Row 1)
In the first step, we get the density in g/L, and the second multiplication converts L to mL.
\[{\rm{d}}\;{\rm{ = }}\,\,\frac{{\rm{m}}}{{\rm{v}}}\,{\rm{ = }}\frac{{{\rm{2}}{\rm{.35}}\,{\rm{g}}}}{{{\rm{0}}{\rm{.035}}\;\cancel{{\rm{L}}}}}\,{\rm{ \times }}\,\frac{{{\rm{1}}\,\cancel{{\rm{L}}}}}{{{\rm{1000}}\,{\rm{mL}}}}{\rm{ = }}\;{\rm{0}}{\rm{.0671}}\,{\rm{g/mL}}\]
Row 2) Remember that 1 cm3 = 1 mL, and therefore, we cancel them.
\[{\rm{m}}\;{\rm{ = }}\,{\rm{d}}\,{\rm{ \times }}\,{\rm{v}}\,{\rm{ = }}\,{\rm{1}}{\rm{.56}}\,\frac{{\cancel{{\rm{g}}}}}{{\cancel{{{\rm{c}}{{\rm{m}}^{\rm{3}}}}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{lb}}}}{{{\rm{453}}{\rm{.6}}\,\cancel{{\rm{g}}}}}\,{\rm{ \times }}\,{\rm{356}}\,\cancel{{{\rm{c}}{{\rm{m}}^{\rm{3}}}}}\,{\rm{ = }}\;{\rm{1}}{\rm{.22}}\;{\rm{lb}}\]
Row 3)
We can convert the units of m and d first, and then plug in the numbers in the formula of volume.
m = 14.6 kg x 1000 = 14600 g
\[{\rm{d}}\;{\rm{ = }}\,{\rm{4}}{\rm{.81}}\,\frac{{\rm{g}}}{{\cancel{{{\rm{mL}}}}}}\;{\rm{ \times }}\;\frac{{{\rm{1000}}\,\cancel{{{\rm{mL}}}}}}{{{\rm{1}}\,\cancel{{\rm{L}}}}}\,{\rm{ \times }}\,\frac{{{\rm{3}}{\rm{.786}}\,\cancel{{\rm{L}}}}}{{{\rm{1}}\,{\rm{gal}}}}{\rm{ = }}\;{\rm{18,211}}\,{\rm{g/gal}}\]
\[{\rm{v}}\;{\rm{ = }}\,\frac{{\rm{m}}}{{\rm{d}}}\,{\rm{ = }}\,\frac{{{\rm{14600}}\,{\rm{g}}}}{{{\rm{18211}}\,{\rm{g/gal}}}}\,{\rm{ = }}\;{\rm{0}}{\rm{.802 gal}}\]
How many kilograms of honey with a density of 1.40 kg/L are there in a gallon container?
5.30 kg
In the first part of the calculation, we convert the units of density to kg/gal, and the last multiplication is to determine the mass in kilograms.
\[{\rm{m}}\;{\rm{ = }}\,{\rm{d}}\,{\rm{ \times }}\,{\rm{v}}\,{\rm{ = }}\,{\rm{1}}{\rm{.40}}\,\frac{{{\rm{kg}}}}{{\cancel{{\rm{L}}}}}\;{\rm{ \times }}\,\frac{{{\rm{3}}{\rm{.786}}\,\cancel{{\rm{L}}}}}{{{\rm{1}}\,\cancel{{{\rm{gal}}}}}}\,{\rm{ \times }}\,{\rm{1}}\,\cancel{{{\rm{gal}}}}\,{\rm{ = }}\;{\rm{5}}{\rm{.30}}\;{\rm{kg}}\]
The density of iron is 8.96 g/cm3. What is its density in pounds per cubic inch (lb/in3)?
0.324 lb/in3
\[{\rm{8}}{\rm{.96}}\,\frac{{\cancel{{\rm{g}}}\,}}{{\cancel{{{\rm{c}}{{\rm{m}}^{\rm{3}}}}}}}\,{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{lb}}}}{{{\rm{453}}{\rm{.6}}\,\cancel{{\rm{g}}}}}{\rm{ \times }}\,\frac{{{\rm{(2}}{\rm{.54}}\,\cancel{{{\rm{cm}}{{\rm{)}}^{\rm{3}}}}}}}{{{{{\rm{(1}}\,{\rm{in)}}}^{\rm{3}}}}}\,{\rm{ = }}\,{\rm{0}}{\rm{.324}}\,{\rm{lb/i}}{{\rm{n}}^{\rm{3}}}\]
The density of iron is 7.86 g/cm3. What is the volume of 5.24 lb of iron expressed in cubic inches?
18.5 in3
The plan would be to convert the mass to grams and use it to calculate the volume which would be in cm3. Once we have this, we can convert it to in3.
\[{\rm{m}}\;{\rm{ = }}\,{\rm{5}}{\rm{.24}}\;\cancel{{{\rm{lb}}}}\,{\rm{ \times }}\;\frac{{{\rm{453}}{\rm{.6}}\,{\rm{g}}}}{{{\rm{1}}\,\cancel{{{\rm{lb}}}}}}\;{\rm{ = }}{\rm{2376}}{\rm{.9}}\,{\rm{g}}\]
\[{\rm{v}}\;{\rm{ = }}\,\frac{{\rm{m}}}{{\rm{d}}}\,{\rm{ = }}\,\frac{{{\rm{2376}}{\rm{.9}}\,{\rm{g}}}}{{{\rm{7}}{\rm{.86}}\,{\rm{g/c}}{{\rm{m}}^{\rm{3}}}}}\,{\rm{ = }}\;{\rm{302}}{\rm{.4 c}}{{\rm{m}}^{\rm{3}}}\]
\[{\rm{v}}\;{\rm{ = }}\,{\rm{302}}{\rm{.4 c}}{{\rm{m}}^{\rm{3}}}\,{\rm{ \times }}\,\frac{{{{\left( {{\rm{1}}\,{\rm{in}}} \right)}^{\rm{3}}}}}{{{{{\rm{(2}}{\rm{.54}}\,{\rm{cm)}}}^{\rm{3}}}}}\; = \;18.5\,{\rm{i}}{{\rm{n}}^{\rm{3}}}\]
A plastic cylinder has a length of 7.25 in, a radius of 1.26 in, and a mass of 841 g. What is the density of the plastic in g/cm3?
1.42 g/cm3
The volume of a cylinder is calculated by the formula v = π · r2 · l. We can either convert the length and radius to cm and determine the volume in cm3, or use the data given in inches, determine the volume in in3 and convert that into cm3.
Let’s go with the second option.
v = π · r2 · l = 3.14 x (1.26)2 in x 7.25 in = 36.1417 in3
Next, we convert the volume to cm3:
\[{\rm{v}}\;{\rm{ = }}\,{\rm{36}}{\rm{.1417 i}}{{\rm{n}}^{\rm{3}}}\,{\rm{ \times }}\,\frac{{{{{\rm{(2}}{\rm{.54}}\,{\rm{cm)}}}^{\rm{3}}}}}{{{{\left( {{\rm{1}}\,{\rm{in}}} \right)}^{\rm{3}}}}}\; = \;592.3\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\]
The last step is to determine the density:
\[{\rm{d}}\;{\rm{ = }}\,\,\frac{{\rm{m}}}{{\rm{v}}}\,{\rm{ = }}\frac{{{\rm{841}}\,{\rm{g}}}}{{{\rm{592}}{\rm{.3}}\;{\rm{c}}{{\rm{m}}^{\rm{3}}}}}\, = \,{\rm{1}}{\rm{.42}}\,{\rm{g/c}}{{\rm{m}}^{\rm{3}}}\]
What is the radius of a steel sphere that has a mass of 65.0 g and a density of 7.86 g/cm3?
1.25 cm
The key here is the formula for the sphere volume:
\[{\rm{v}}\;{\rm{ = }}\,\frac{{\rm{4}}}{{\rm{3}}}\;{\rm{\pi }}\,{{\rm{r}}^{\rm{3}}}\]
We can rearrange the equation to get an expression for r and the only missing value would be the volume of the sphere which we can calculate from the mass and the density.
\[{\rm{v}}\;{\rm{ = }}\,\frac{{\rm{m}}}{{\rm{d}}}\,{\rm{ = }}\,\frac{{{\rm{65}}\,{\rm{g}}}}{{{\rm{7}}{\rm{.86}}\,{\rm{g/c}}{{\rm{m}}^{\rm{3}}}}}\,{\rm{ = }}\;{\rm{8}}{\rm{.2697 c}}{{\rm{m}}^{\rm{3}}}\]
The expression for r would be:
\[\sqrt[{\rm{3}}]{{\frac{{{\rm{3v}}}}{{{\rm{4\pi }}}}\;{\rm{ = }}\;}}\sqrt[{\rm{3}}]{{\frac{{{\rm{3}}\,{\rm{ \times }}\;{\rm{8}}{\rm{.2697}}\,{\rm{c}}{{\rm{m}}^{\rm{3}}}}}{{{\rm{4}}\,{\rm{ \times }}\,{\rm{3}}{\rm{.14}}}}\;{\rm{ = }}\;}}{\rm{1}}{\rm{.25}}\,{\rm{cm}}\]