All the measurements such as quantity, length, and volume are given with a number and a unit. For example, 2.5 lb, 35 miles, 15 gallons and etc. Now, these units are familiar to you if you live in a country that uses the English system, but they may not be as evident for someone who is in a country where the metric system is used. Kilogram, centimeter, and Celsius which are the measuring units there are probably just as foreign to you.
This issue of having inconsistent units spread to scientists too as they were not able to communicate their data accurately across research groups in different countries and therefore, the International System of Units (SI), was set to be the standard for communication. It is based on the metric system, and in today’s article, we will learn some strategies for converting different units including the metric ones.
Dimensional Analysis
The most common tool used for converting units is the dimensional analysis and it is a convenient approach for doing that. The only thing we need for dimensional analysis is what is called conversion factors and correctly picking them for our conversions.
So, what is a conversion factor?
These are essentially the ratios of the units for the given quantity.
For example, we know that 1 ft is 12 in, and therefore, we can derive two conversion factors by simply getting the ratio of these units:
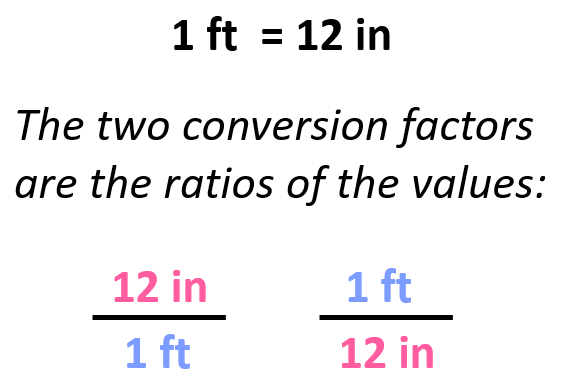
Once we have the conversion factor, we can convert a quantity given in one unit into an equivalent quantity with a different unit by multiplying it with the correct factor.
Let’s say we need to calculate how many inches 4.58 ft is.
The first step is to write the conversion factors, and we have already got for the ft-in relationship:
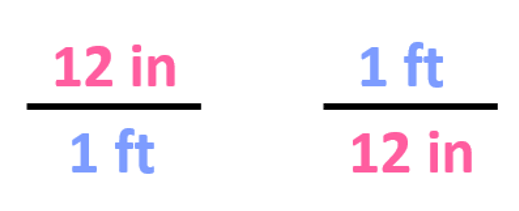
Step 2. Choose the correct conversion factor. The idea is that we need to cancel the original units into final units which means we need to pick the conversion factor where the initial unit is in the denominator. In this case, it is the second conversion factor since it allows to cancel the ft:
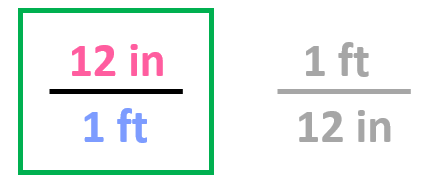
All we need to do at this point is multiply the initial number with the conversion factor:
Notice that we kept 3 significant figures even though 12 in has only two as written. The reason for this is the conversion factors have an infinite number of significant figures because they are not measured but rather set numbers. In other words, nobody is using a ruler with limited accuracy to tell how many significant figures they think it has. So, for your calculations, the number of significant figures is always going to be limited by the given number and not the conversion factors.
Summarizing what we did, we can write the steps as follows:
Below are some of the common conversion factors for the length that you are going to need in a general chemistry class:
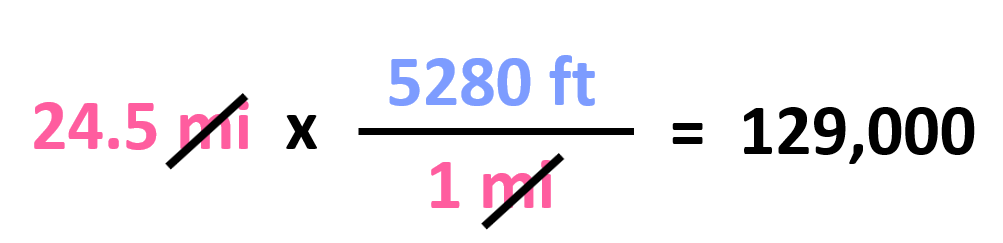
Let’s now try to convert 241 miles to ft.
First, we find that 1 mi is 5280 ft, and therefore, the conversion factors are:
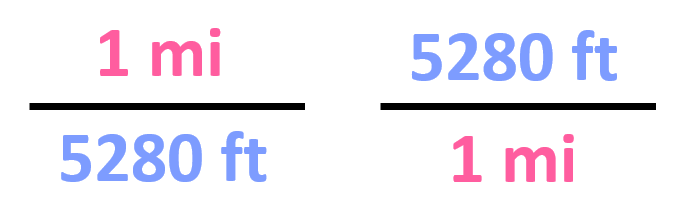
Out of these, we need to pick the second one since it has the mi in the denominator, and we can cancel them with the initial data:
Multi-Step Unit Conversion
Sometimes, you may not be given a conversion factor between two units. For example, how many inches is 2.68 km?
In these cases, you will need to link the units through in more than one conversion. We can find from the table that 1 km is 1000 m, and 1 m is 100 cm which in turn can be converted to inches because we find that 1 in = 2.54 cm. So, the plan is km → m → cm → in.
A great thing about dimensional analysis is that we can combine all the steps in one operation by simply adding the correct conversion factors one by one.
You can first write the initial number with the unit, and add a fraction with just units in the correct place:
And once we know which units go to the denominator, we can write the correct conversion factors from the table:
Another example, convert 1459 km to yards given that 1 m = 1.09361 yd.
The plan here would be going from km to m, and m to yd.
Keep in mind that there might be several ways of going about the same conversion depending on what factors we have. For example, if we did not have the m-yd conversion, we could go km → m → cm → in → ft → yd based on the data we have in the table.
Converting Mass Units
There is no difference in what units you are converting – dimensional analysis is always based on the same strategy.
For example, how many kilograms is 6.85 lb?
Here are some conversion numbers for mass units that we can use to pick suitable factors:
Based on these, we can set up a plan lb → g → kg:
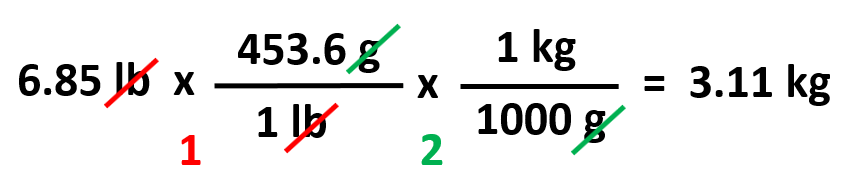
Converting Volume Units
Unlike the mass and the length, there are two types of units for the volume. In one of them, the volume is given in a simple unit such as L, mL, or gallon, which already presume a volume, and the other is when the volume is given cubes. This, in general, is referred to units raised to a power, and for volume, it is the cube.
Let’s do an example with a simple volume unit conversion first.
Using the conversion factors given below, calculate the volume of 5.26 L water in gallons.
To find the correct conversion factors, first look for a unit that is correlated to liters. In this table, it is the qt which is then linked to gallons. Therefore, we can write a two-step conversion using dimensional analysis:
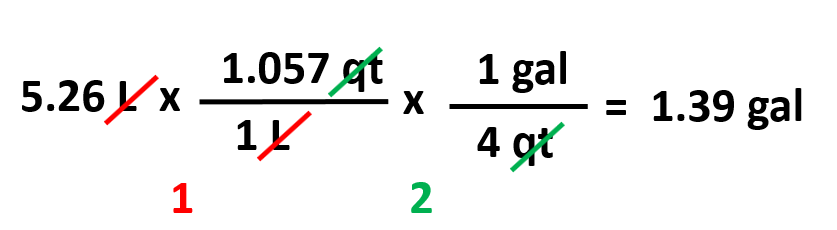
Converting Units Raised to Power
The most important thing you need to remember here is to raise both the number and unit to the given power. For example, if 1 in = 2.54 cm, then
Do not confuse this when the problem says, for example, how many cm2 is 15 in2. You do not want to square 15 because that number whatever it was is already squared and it is the final number with the squared unit. So, to find this in cm2, we write:
Converting Volume Units Raised to Power
What is the volume of a textbook in cm3 if the sides are 10.5 and 7.90 in respectively and the thickness is 1.85 in?
We can first calculate the volume in in3 by multiplying the sides and the thickness:
V (in3) = 10.5 in x 7.90 in x 1.85 in = 153.46 in3
Next, we use dimensional analysis to convert in3 to cm3:
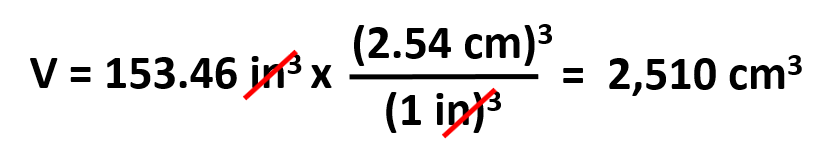
Converting Quantitates with Two Units
A good example of measurements with two units is the speed which is described by the ratio of distance over time. For example, 75 mi/h means the vehicle goes 75 mi per hour. So, let’s say we are asked to express this speed in m/s.
This may look confusing at first, but don’t worry – we are going to follow exactly what we have been doing for converting one unit. The only difference is that we repeat the process for the two units as if we are converting separate units. It does not matter which you nit you start with, so we can go with the miles. The conversion plan for miles to meters would be mi → km → m, and therefore we can write the first part as:
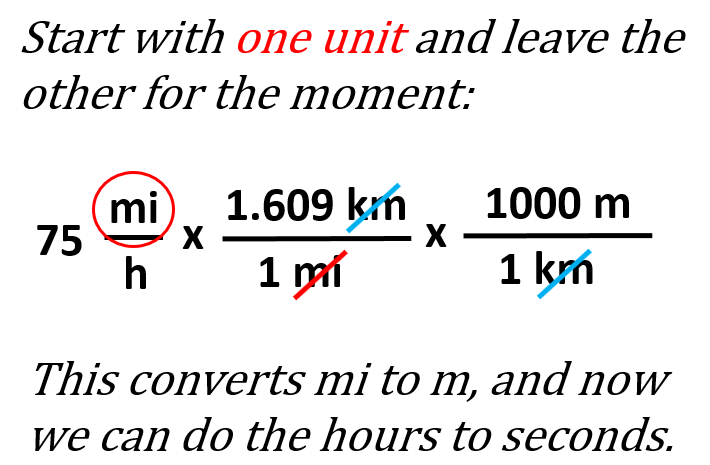
This part converts the miles to meters and next, we do the same for the hours-seconds by simply adding the conversion factors:
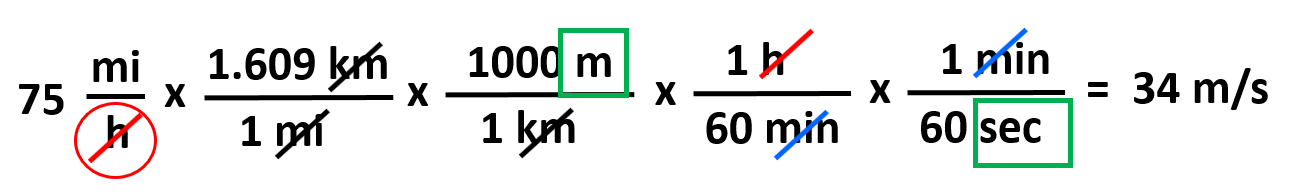
So, the first part gets us to meters, and the second part converts the hours to seconds. Notice that because the hour is in the denominator, place it at the top and the minute at the bottom for the first conversion factor.
Check Also
Practice
Perform each of the following conversions.
a) 5.98 cm to millimeters
b) 65 cm to meters
c) 487 mm to inches (1 in = 2.54 cm, 1 cm = 10 mm)
d) 2894 ft to kilometers (1 mi = 1.609 km)
e) 6854 m to miles (1 mi = 1.609 km)
f) 548 lb to kilograms
g) 451 oz to kilograms
h) 1564 mL to gallons (1 gal = 3.785 L)
i) 659 mL to quarts
j) 72 gal to milliliters
k) 482 lb to grams
l) 54 quarts to milliliters
59.8 mm
0.0365 m
0.192 in
0.882 km
4.26 mi
250. kg
12.9 kg
0.413 gal
0.697 qt
3.30 x 104 mL
2.20 x 105 g
5.1 x 104 mL
a) 98 cm to millimeters
1 cm = 10 mm, therefore:
\[{\rm{5}}{\rm{.98}}\,\cancel{{{\rm{cm}}}}\;{\rm{ \times }}\,\frac{{{\rm{10}}\,{\rm{mm}}}}{{{\rm{1}}\,\cancel{{{\rm{cm}}}}}}\;{\rm{ = }}\;{\rm{59}}{\rm{.8}}\,{\rm{mm}}\]
b) 65 cm to meters
1 m = 100 cm, therefore:
\[{\rm{3}}{\rm{.65}}\,\cancel{{{\rm{cm}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{m}}}}{{{\rm{100}}\,\cancel{{{\rm{cm}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.0365}}\,{\rm{m}}\]
c) 487 mm to inches (1 in = 2.54 cm, 1 cm = 10 mm)
\[{\rm{4}}{\rm{.87}}\,\cancel{{{\rm{mm}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\,\cancel{{{\rm{cm}}}}}}{{{\rm{10}}\,\cancel{{{\rm{mm}}}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{in}}}}{{{\rm{2}}{\rm{.54}}\,\cancel{{{\rm{cm}}}}}}{\rm{ = }}\;{\rm{0}}{\rm{.192}}\,{\rm{in}}\]
d) 2894 ft to kilometers (1 mi = 1.609 km)
\[{\rm{2894}}\,\cancel{{{\rm{ft}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\,\cancel{{{\rm{mi}}}}}}{{{\rm{5280}}\,\cancel{{{\rm{ft}}}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}{\rm{.609}}\,{\rm{km}}}}{{{\rm{1}}\,\cancel{{{\rm{mi}}}}}}{\rm{ = }}\;{\rm{0}}{\rm{.882}}\,{\rm{km}}\]
e) 6854 m to miles (1 mi = 1.609 km)
\[{\rm{6854}}\,\cancel{{\rm{m}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\,\cancel{{{\rm{km}}}}}}{{{\rm{1000}}\,\cancel{{\rm{m}}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{mi}}}}{{{\rm{1}}{\rm{.609}}\,\cancel{{{\rm{km}}}}}}{\rm{ = }}\;{\rm{4}}{\rm{.26}}\,{\rm{mi}}\]
f) 548 lb to kilograms
\[{\rm{548}}\,\cancel{{{\rm{lb}}}}\;{\rm{ \times }}\,\frac{{{\rm{456}}{\rm{.3}}\,\cancel{{\rm{g}}}}}{{{\rm{1}}\,\cancel{{{\rm{lb}}}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{kg}}}}{{{\rm{1000}}\,\cancel{{\rm{g}}}}}{\rm{ = }}\;{\rm{250}}{\rm{.}}\,{\rm{kg}}\]
g) 451 oz to kilograms
\[{\rm{451}}\,\cancel{{{\rm{oz}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\,\cancel{{{\rm{lb}}}}}}{{{\rm{16}}\,\cancel{{{\rm{oz}}}}}}\;{\rm{ \times }}\,\frac{{{\rm{456}}{\rm{.3}}\,\cancel{{\rm{g}}}}}{{{\rm{1}}\,\cancel{{{\rm{lb}}}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{kg}}}}{{{\rm{1000}}\,\cancel{{\rm{g}}}}}{\rm{ = }}\;{\rm{12}}{\rm{.9}}\,{\rm{kg}}\]
h) 1564 mL to gallons (1 gal = 3.785 L)
\[{\rm{1564}}\,\cancel{{{\rm{mL}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\,\cancel{{\rm{L}}}}}{{{\rm{1000}}\,\cancel{{{\rm{mL}}}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{gal}}}}{{{\rm{3}}{\rm{.785}}\,\cancel{{\rm{L}}}}}{\rm{ = }}\;{\rm{0}}{\rm{.413}}\,{\rm{gal}}\]
i) 659 mL to quarts
\[{\rm{659}}\,\cancel{{{\rm{mL}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\,\cancel{{\rm{L}}}}}{{{\rm{1000}}\,\cancel{{{\rm{mL}}}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}{\rm{.057}}\,{\rm{qt}}}}{{{\rm{1}}\,\cancel{{\rm{L}}}}}{\rm{ = }}\;{\rm{0}}{\rm{.697}}\,{\rm{qt}}\]
j) 72 gal to milliliters
\[{\rm{8}}{\rm{.72}}\,\cancel{{{\rm{gal}}}}\;{\rm{ \times }}\,\frac{{{\rm{4}}\,\cancel{{{\rm{qt}}}}}}{{{\rm{1}}\,\cancel{{{\rm{gal}}}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\,\cancel{{\rm{L}}}}}{{{\rm{1}}{\rm{.057}}\,{\rm{qt}}}}{\rm{ \times }}\,\frac{{{\rm{1000}}\,{\rm{mL}}}}{{{\rm{1}}\,\cancel{{\rm{L}}}}}{\rm{ = }}\;{\rm{3}}{\rm{.30}}\, \times \,{\rm{1}}{{\rm{0}}^{\rm{4}}}\,{\rm{mL}}\]
k) 482 lb to grams
\[{\rm{482}}\,\cancel{{{\rm{lb}}}}\;{\rm{ \times }}\,\frac{{{\rm{456}}{\rm{.3}}\;{\rm{g}}}}{{{\rm{1}}\,\cancel{{{\rm{lb}}}}}}\;{\rm{ = }}\;219,936\; = \,{\rm{2}}{\rm{.20}}\, \times \,{\rm{1}}{{\rm{0}}^{\rm{5}}}\,{\rm{g}}\]
l) 54 quarts to milliliters
\[{\rm{54}}\,\cancel{{{\rm{qt}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\,\cancel{{\rm{L}}}}}{{{\rm{1}}{\rm{.057}}\,\cancel{{{\rm{qt}}}}}}{\rm{ \times }}\,\frac{{{\rm{1000}}\,{\rm{mL}}}}{{{\rm{1}}\,\cancel{{\rm{L}}}}}{\rm{ = }}\;51,088\; = \;5.1\, \times \,{10^4}\,{\rm{mL}}\]
How many dozen eggs are in 15,652 eggs?
1304 dozens
1 dozen = 12, therefore:
\[{\rm{15,652}}\,\cancel{{{\rm{eggs}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{dozen}}}}{{{\rm{12}}\,\cancel{{{\rm{eggs}}}}}}\;{\rm{ = }}\;1,304.3\,{\rm{dozen}}\]
How many years are in 5,489 days?
15.04 years
\[{\rm{5,489}}\,\cancel{{{\rm{days}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{year}}}}{{{\rm{365}}\,\cancel{{{\rm{days}}}}}}\;{\rm{ = }}\;{\rm{15}}{\rm{.04}}\;{\rm{years}}\]
How many weeks are in 2.5 centuries? (1 yr. = 52 weeks)
13,000 weeks
\[{\rm{2}}{\rm{.5}}\,\cancel{{{\rm{century}}}}\;{\rm{ \times }}\,\frac{{{\rm{100}}\,\cancel{{{\rm{years}}}}}}{{{\rm{1}}\,\cancel{{{\rm{century}}}}}}{\rm{ \times }}\,\frac{{{\rm{52}}\,{\rm{weaks}}}}{{{\rm{1}}\,\cancel{{{\rm{year}}}}}}{\rm{ = }}\;{\rm{13,000}}\,{\rm{weaks}}\]
Units Raised to a Power
Perform each of the following conversions.
a) 45 cm2 to in2
b) 59 mm2 to ft2
c) 995 ft2 to m2
d) 2.54 dm3 to in3 (1 dm = 10 cm)
e) 4.22 gallons to cm3 (1 L = 1000 cm3)
f) 5.64 L to ft3
7.0 in2
6.35 x 10-4 ft2
92.4 m2
155 in3
1.60 x 104 cm3
0.199 ft3
Remember to apply the exponent to the number and the unit!
a)
\[{\rm{45}}\;{\rm{c}}{{\rm{m}}^{\rm{2}}}\;{\rm{ \times }}\,\frac{{{{{\rm{(1}}\,{\rm{in)}}}^{\rm{2}}}}}{{{{{\rm{(2}}{\rm{.54}}\,{\rm{cm)}}}^{\rm{2}}}}}\; = \;{\rm{45}}\;\cancel{{{\rm{c}}{{\rm{m}}^{\rm{2}}}}}\, \times \;\frac{{{\rm{1}}\,{\rm{i}}{{\rm{n}}^{\rm{2}}}}}{{{\rm{6}}{\rm{.4516}}\,\cancel{{{\rm{c}}{{\rm{m}}^{\rm{2}}}}}}}\; = \,7.0\,{\rm{i}}{{\rm{n}}^{\rm{2}}}\]
b)
\[{\rm{59}}\;{\rm{m}}{{\rm{m}}^{\rm{2}}}\;{\rm{ \times }}\,\frac{{{{{\rm{(1}}\,{\rm{cm)}}}^{\rm{2}}}}}{{{{{\rm{(10}}\,{\rm{mm)}}}^{\rm{2}}}}}\;{\rm{ \times }}\,\frac{{{{{\rm{(1}}\,{\rm{in)}}}^{\rm{2}}}}}{{{{{\rm{(2}}{\rm{.54}}\,{\rm{cm)}}}^{\rm{2}}}}}\,{\rm{ \times }}\,\frac{{{{{\rm{(1}}\,{\rm{ft)}}}^{\rm{2}}}}}{{{{{\rm{(12}}\,{\rm{in)}}}^{\rm{2}}}}}\]
\[{\rm{59}}\;\cancel{{{\rm{m}}{{\rm{m}}^{\rm{2}}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\,\cancel{{{\rm{c}}{{\rm{m}}^{\rm{2}}}}}}}{{{\rm{100}}\,\cancel{{{\rm{m}}{{\rm{m}}^{\rm{2}}}}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\,\cancel{{{\rm{i}}{{\rm{n}}^{\rm{2}}}}}}}{{{\rm{6}}{\rm{.4516}}\,\cancel{{{\rm{c}}{{\rm{m}}^{\rm{2}}}}}}}\,{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{f}}{{\rm{t}}^{\rm{2}}}}}{{{\rm{144}}\,\cancel{{{\rm{i}}{{\rm{n}}^{\rm{2}}}}}}}\; = \,6.35\, \times \;{10^{ – 4}}\,{\rm{f}}{{\rm{t}}^{\rm{2}}}\]
c)
\[{\rm{995}}\;{\rm{f}}{{\rm{t}}^{\rm{2}}}\;{\rm{ \times }}\,\frac{{{{{\rm{(12}}\,{\rm{in)}}}^{\rm{2}}}}}{{{{{\rm{(1}}\,{\rm{ft)}}}^{\rm{2}}}}}\,{\rm{ \times }}\,\frac{{{{{\rm{(2}}{\rm{.54}}\,{\rm{cm)}}}^{\rm{2}}}}}{{{{{\rm{(12}}\,{\rm{in)}}}^{\rm{2}}}}}\,{\rm{ \times }}\,\frac{{{{{\rm{(1}}\,{\rm{m)}}}^{\rm{2}}}}}{{{{{\rm{(100}}\,{\rm{cm)}}}^{\rm{2}}}}}\]
\[{\rm{995}}\;\cancel{{{\rm{f}}{{\rm{t}}^{\rm{2}}}}}\;{\rm{ \times }}\,\frac{{{\rm{144}}\,\cancel{{{\rm{i}}{{\rm{n}}^{\rm{2}}}}}}}{{{\rm{1}}\,\cancel{{{\rm{f}}{{\rm{t}}^{\rm{2}}}}}}}\,{\rm{ \times }}\,\frac{{{\rm{6}}{\rm{.4516}}\,\cancel{{{\rm{c}}{{\rm{m}}^{\rm{2}}}}}}}{{{\rm{1}}\,\cancel{{{\rm{i}}{{\rm{n}}^{\rm{2}}}}}}}\,{\rm{ \times }}\,\frac{{{\rm{1}}\,{{\rm{m}}^{\rm{2}}}}}{{{\rm{10000}}\,\cancel{{{\rm{c}}{{\rm{m}}^{\rm{2}}}}}}}\, = \,92.4\,{{\rm{m}}^{\rm{2}}}\]
d)
\[{\rm{2.54}}\;{\rm{d}}{{\rm{m}}^{\rm{3}}}\;{\rm{ \times }}\,\frac{{{{{\rm{(10}}\,{\rm{cm)}}}^{\rm{3}}}}}{{{{{\rm{(1}}\,{\rm{dm)}}}^{\rm{3}}}}}\,{\rm{ \times }}\,\frac{{{{{\rm{(1}}\,{\rm{in)}}}^{\rm{3}}}}}{{{{{\rm{(2}}{\rm{.54}}\,{\rm{cm)}}}^{\rm{3}}}}}\,\]
\[{\rm{2}}{\rm{.54}}\;\cancel{{{\rm{d}}{{\rm{m}}^{\rm{3}}}}}\;{\rm{ \times }}\,\frac{{{\rm{1000}}\,\cancel{{{\rm{c}}{{\rm{m}}^{\rm{3}}}}}}}{{{\rm{1}}\,\cancel{{{\rm{d}}{{\rm{m}}^{\rm{3}}}}}}}\,{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{i}}{{\rm{n}}^{\rm{3}}}}}{{{\rm{16}}{\rm{.387}}\,\cancel{{{\rm{c}}{{\rm{m}}^{\rm{3}}}}}}}\; = \,155\,{\rm{i}}{{\rm{n}}^{\rm{3}}}\]
e) 4.22 gallons to cm3 (1 L = 1000 cm3)
\[{\rm{4}}{\rm{.22}}\;\cancel{{{\rm{gal}}}}\;{\rm{ \times }}\,\frac{{{\rm{4}}\,\cancel{{{\rm{qt}}}}}}{{{\rm{1}}\,\cancel{{{\rm{gal}}}}}}\,{\rm{ \times }}\,\frac{{{\rm{1}}\,\cancel{{\rm{L}}}{\rm{ }}}}{{{\rm{1}}{\rm{.057 }}\cancel{{{\rm{qt}}}}}}\,{\rm{ \times }}\;\frac{{{\rm{1000}}\,{\rm{c}}{{\rm{m}}^{\rm{3}}}{\rm{ }}}}{{{\rm{1}}\,\cancel{{\rm{L}}}}}\; = \,15,970\, = \;1.60\, \times \,{10^4}\,\]
f) 64 L to ft3
One unit is raised to a power, and therefore, we need to look up what length unit is correlated to liters when cubed. From the conversion factors, we find that 1 L = 1000 cm3, and once we convert L to cm3, it is like converting cm to ft. Remember to apply the exponent to the number and the unit.
\[{\rm{5}}{\rm{.64}}\;\cancel{{\rm{L}}}\;{\rm{ \times }}\,\frac{{{\rm{1000}}\,{\rm{c}}{{\rm{m}}^{\rm{3}}}{\rm{ }}}}{{{\rm{1}}\,\cancel{{\rm{L}}}}}\;{\rm{ \times }}\,\frac{{{{{\rm{(1}}\,{\rm{in)}}}^{\rm{3}}}}}{{{{{\rm{(2}}{\rm{.54}}\,{\rm{cm)}}}^{\rm{3}}}}}\,{\rm{ \times }}\,\frac{{{{{\rm{(1}}\,{\rm{ft)}}}^{\rm{3}}}}}{{{{{\rm{(12}}\,{\rm{in)}}}^{\rm{3}}}}}\]
\[{\rm{5}}{\rm{.64}}\;\cancel{{\rm{L}}}\;{\rm{ \times }}\,\frac{{{\rm{1000}}\,\cancel{{{\rm{c}}{{\rm{m}}^{\rm{3}}}}}{\rm{ }}}}{{{\rm{1}}\,\cancel{{\rm{L}}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\,\cancel{{{\rm{i}}{{\rm{n}}^{\rm{3}}}}}}}{{{\rm{16}}{\rm{.387}}\,\cancel{{{\rm{c}}{{\rm{m}}^{\rm{3}}}}}}}\,{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{f}}{{\rm{t}}^{\rm{3}}}}}{{{\rm{1728}}\,\cancel{{{\rm{i}}{{\rm{n}}^{\rm{3}}}}}}}\; = \;0.199\,{\rm{f}}{{\rm{t}}^{\rm{3}}}\]
Would 550 m2 of fabric be enough to upholster 200 chairs if each requires 35.4 ft2 fabric?
The material won’t be enough.
We can first determine how many ft2 of fabric is needed for 200 chairs, and then compare it to 150 m2 by convert the units of either.
200 x 35.4 ft2 = 7080 ft2
Let’s now convert this to m2 according to this plan:
\[{\rm{995}}\;{\rm{f}}{{\rm{t}}^{\rm{2}}}\;{\rm{ \times }}\,\frac{{{{{\rm{(12}}\,{\rm{in)}}}^{\rm{2}}}}}{{{{{\rm{(1}}\,{\rm{ft)}}}^{\rm{2}}}}}\,{\rm{ \times }}\,\frac{{{{{\rm{(2}}{\rm{.54}}\,{\rm{cm)}}}^{\rm{2}}}}}{{{{{\rm{(12}}\,{\rm{in)}}}^{\rm{2}}}}}\,{\rm{ \times }}\,\frac{{{{{\rm{(1}}\,{\rm{m)}}}^{\rm{2}}}}}{{{{{\rm{(100}}\,{\rm{cm)}}}^{\rm{2}}}}}\]
\[{\rm{7080}}\;\cancel{{{\rm{f}}{{\rm{t}}^{\rm{2}}}}}\;{\rm{ \times }}\,\frac{{{\rm{144}}\,\cancel{{{\rm{i}}{{\rm{n}}^{\rm{2}}}}}}}{{{\rm{1}}\,\cancel{{{\rm{f}}{{\rm{t}}^{\rm{2}}}}}}}\,{\rm{ \times }}\,\frac{{{\rm{6}}{\rm{.4516}}\,\cancel{{{\rm{c}}{{\rm{m}}^{\rm{2}}}}}}}{{{\rm{1}}\,\cancel{{{\rm{i}}{{\rm{n}}^{\rm{2}}}}}}}\,{\rm{ \times }}\,\frac{{{\rm{1}}\,{{\rm{m}}^{\rm{2}}}}}{{{\rm{10000}}\,\cancel{{{\rm{c}}{{\rm{m}}^{\rm{2}}}}}}}\, = \,658\,{{\rm{m}}^{\rm{2}}}\]
200 chairs will require 658 m2 of fabric, therefore, the material won’t be enough.
Convert 16.4 cubic decimeters (16.4 dm3) to gallons, using the following conversion factors:
2.54 cm = 1 in, 231 in3 = 1 gallon, 1 dm = 10 cm
4.33 gal
\[{\rm{16}}{\rm{.4}}\;{\rm{d}}{{\rm{m}}^{\rm{3}}}\;{\rm{ \times }}\,\frac{{{{{\rm{(10}}\,{\rm{cm)}}}^{\rm{3}}}}}{{{{{\rm{(1}}\,{\rm{dm)}}}^{\rm{3}}}}}\,{\rm{ \times }}\,\frac{{{{{\rm{(1}}\,{\rm{in)}}}^{\rm{3}}}}}{{{{{\rm{(2}}{\rm{.54}}\,{\rm{cm)}}}^{\rm{3}}}}}\,{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{gal}}}}{{{\rm{231}}\,{\rm{i}}{{\rm{n}}^{\rm{3}}}}}\]
\[{\rm{16}}{\rm{.4}}\;{\rm{d}}{{\rm{m}}^{\rm{3}}}\;{\rm{ \times }}\,\frac{{{\rm{1000}}\,{\rm{c}}{{\rm{m}}^{\rm{3}}}}}{{{\rm{1}}\,{\rm{d}}{{\rm{m}}^{\rm{3}}}}}\,{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{i}}{{\rm{n}}^{\rm{3}}}}}{{{\rm{16}}{\rm{.387}}\,{\rm{c}}{{\rm{m}}^{\rm{3}}}}}\,{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{gal}}}}{{{\rm{231}}\,{\rm{i}}{{\rm{n}}^{\rm{3}}}}}\;{\rm{ = }}\;{\rm{4}}{\rm{.33}}\,{\rm{gal}}\]
Converting Two Units
8) Perform each of the following conversions.
a) 195 cm/s to mi/h
b) 55 km/h to yd/min (1 m = 1.094 yd)
c) 45 mi/h to m/s
4.36 mi/h
1.00 x 103 yd/min
20.1 m/s
a) 195 cm/s to mi/h
The plan is to first convert cm to mi and then sec to hours.
\[{\rm{195}}\,\frac{{\cancel{{{\rm{cm}}}}}}{{\cancel{{{\rm{sec}}}}}}\,{\rm{ \times }}\,\frac{{{\rm{1}}\,\cancel{{\rm{m}}}}}{{{\rm{100}}\,\cancel{{{\rm{cm}}}}}}{\rm{ \times }}\,\frac{{{\rm{1}}\,\cancel{{{\rm{km}}}}}}{{{\rm{1000}}\,\cancel{{\rm{m}}}}}\,{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{mi}}}}{{{\rm{1}}{\rm{.609}}\,\cancel{{{\rm{km}}}}}}{\rm{ \times }}\,\frac{{{\rm{60}}\,\cancel{{{\rm{sec}}}}}}{{{\rm{1}}\,\cancel{{{\rm{min}}}}}}{\rm{ \times }}\,\frac{{{\rm{60}}\,\cancel{{{\rm{min}}}}}}{{{\rm{1}}\,{\rm{h}}}}{\rm{ = }}\;{\rm{4}}{\rm{.36}}\,{\rm{mi/h}}\]
b) 55 km/h to yd/min (1 m = 1.094 yd)
\[{\rm{55}}\,\frac{{\cancel{{{\rm{km}}}}}}{{\cancel{{\rm{h}}}}}\,{\rm{ \times }}\,\frac{{{\rm{1000}}\,\cancel{{\rm{m}}}}}{{{\rm{1}}\,\cancel{{{\rm{km}}}}}}{\rm{ \times }}\,\frac{{{\rm{1}}{\rm{.094}}\,{\rm{yd}}}}{{{\rm{1}}\,\cancel{{\rm{m}}}}}\,{\rm{ \times }}\,\frac{{{\rm{1}}\,\cancel{{\rm{h}}}}}{{{\rm{60}}\,{\rm{min}}}}{\rm{ = }}\;{\rm{1}}{\rm{.00 }} \times \;{\rm{1}}{{\rm{0}}^{\rm{3}}}\,{\rm{yd/min}}\]
c) 45 mi/h to m/s
\[{\rm{45}}\,\frac{{\cancel{{{\rm{mi}}}}}}{{\cancel{{\rm{h}}}}}\,{\rm{ \times }}\,\frac{{{\rm{1}}{\rm{.609}}\,\cancel{{{\rm{km}}}}}}{{{\rm{1}}\,\cancel{{{\rm{mi}}}}}}{\rm{ \times }}\,\frac{{{\rm{1000}}\,{\rm{m}}}}{{{\rm{1}}\,\cancel{{{\rm{km}}}}}}\,{\rm{ \times }}\,\frac{{{\rm{1}}\,\cancel{{\rm{h}}}}}{{{\rm{60}}\,\cancel{{{\rm{min}}}}}}{\rm{ \times }}\,\frac{{{\rm{1}}\,\cancel{{{\rm{min}}}}}}{{{\rm{60}}\,{\mathop{\rm s}\nolimits} }}{\rm{ = }}\;{\rm{20}}{\rm{.1}}\,{\rm{m/s}}\]
The world record for 100-m dash is 8.58 s. Calculate the average speed of the athlete in mi/h.
26.1 mi/h
The speed is 100 m/8.58 s = 11.66 m/s, and this is what we need to convert to mi/h.
\[{\rm{100}}\,\frac{{\cancel{{\rm{m}}}}}{{{\rm{8}}{\rm{.58}}\,\cancel{{\rm{s}}}}}\,{\rm{ \times }}\,\frac{{{\rm{1}}\,\cancel{{{\rm{km}}}}}}{{{\rm{1000}}\,\cancel{{\rm{m}}}}}\,{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{mi}}}}{{{\rm{1}}{\rm{.609}}\,\cancel{{{\rm{km}}}}}}{\rm{ \times }}\,\frac{{{\rm{60}}\,\cancel{{\rm{s}}}}}{{{\rm{1}}\,\cancel{{{\rm{min}}}}}}{\rm{ \times }}\,\frac{{{\rm{60}}\,\cancel{{{\rm{min}}}}}}{{{\rm{1}}\,{\rm{h}}}}{\rm{ = }}\;{\rm{26}}{\rm{.1}}\,{\rm{mi/h}}\]
Assuming constant speed, how long will it take for the athlete to run 500. m if she runs the 100-yard dash in 12.0 s?
65.6 s
We can convert the given speed 100 yd/12.0 s to m/s and then the 500 m by this to get the time.
\[\frac{{\,{\rm{100}}\cancel{{{\rm{yd}}}}}}{{{\rm{12}}\;{\rm{s}}}}\,{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{m}}}}{{{\rm{1}}{\rm{.094}}\,\cancel{{{\rm{yd}}}}}}{\rm{ = }}\;{\rm{7}}{\rm{.617}}\,{\rm{m/s}}\]
So, the athlete runs 7.617 meters in one second, therefore, if we divide 500 by 7.617:
\[{\rm{500}}\,{\rm{m}}\,{\rm{ \div }}\frac{{\,{\rm{7}}{\rm{.617}}\,{\rm{m}}}}{{\rm{s}}}\,{\rm{ = }}\,\,{\rm{500}}\,\cancel{{\rm{m}}}\,{\rm{ \times }}\frac{{{\rm{s}}\,}}{{{\rm{7}}{\rm{.617}}\,\cancel{{\rm{m}}}}}{\rm{ = 65}}{\rm{.6s}}\]
We could also convert 500 m to yards, and then divide this by the speed given as 100 yd/12 s, which is one conversion would look like:
\[{\rm{500}}\,\cancel{{\rm{m}}}\,{\rm{ \times }}\,\frac{{{\rm{1}}{\rm{.094}}\,\cancel{{{\rm{yd}}}}}}{{{\rm{1}}\,\cancel{{\rm{m}}}}}\,{\rm{ \times }}\,\frac{{{\rm{12}}\,{\rm{s}}\,}}{{{\rm{100}}\,\cancel{{{\rm{yd}}}}}}{\rm{ = 65}}{\rm{.6s}}\]
Notice that the last step is dividing the distance by the speed, and it is reversed in order to perform multiplication.
Ho many liters of soda will be needed for 50 guests if each of them drinks 10. fl. oz. of soda?
14.8 L
First multiply 10 fl oz by 50 to find how many fl oz of soda is needed for all the gests, and then we convert it to liters. (1 fl oz = 29.6 mL)
\[{\rm{50}}\,\cancel{{{\rm{guests}}}}\,{\rm{ \times }}\,\frac{{{\rm{10}}{\rm{.}}\,\cancel{{{\rm{fl}}\,{\rm{oz}}}}}}{{{\rm{1}}\,\cancel{{{\rm{guest}}}}}}\,{\rm{ \times }}\,\frac{{{\rm{29}}{\rm{.6}}\,\cancel{{{\rm{mL}}}}\,}}{{{\rm{1}}\,\cancel{{{\rm{fl}}\,{\rm{oz}}}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\;{\rm{L}}\,}}{{{\rm{1000}}\,\cancel{{{\rm{mL}}}}}}{\rm{ = 14}}{\rm{.8}}\,{\rm{L}}\]
What is the speed of a car in cm/s if it goes 25 mi/h?
11.2 m/s
The plan is to first convert mi to m, and then hours to sec.
\[{\rm{25}}\,\frac{{\cancel{{{\rm{mi}}}}}}{{\cancel{{\rm{h}}}}}\,{\rm{ \times }}\,\frac{{{\rm{1}}{\rm{.609}}\,\cancel{{{\rm{km}}}}}}{{{\rm{1}}\,\cancel{{{\rm{mi}}}}}}\,{\rm{ \times }}\,\frac{{{\rm{1000}}\,{\rm{m}}}}{{{\rm{1}}\,\cancel{{{\rm{km}}}}}}{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{h}}}}{{{\rm{60}}\,\cancel{{{\rm{min}}}}}}\,{\rm{ \times }}\,\frac{{{\rm{1}}\,\cancel{{{\rm{min}}}}}}{{{\rm{60}}\,{\rm{s}}}}\,{\rm{ = }}\;{\rm{11}}{\rm{.2}}\,{\rm{m/s}}\]
Would a car traveling at a constant speed of 62 km/h violate a 40 mi/h speed limit?
The speed is slightly over the limit.
We can convert the speed to mi/h and compare with the speed limit given in mi/h.
\[{\rm{62}}\,\frac{{\cancel{{{\rm{km}}}}}}{{\rm{h}}}\,{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{mi}}}}{{{\rm{1}}{\rm{.609}}\,\cancel{{{\rm{km}}}}}}\,{\rm{ = }}\;{\rm{38}}{\rm{.5}}\,{\rm{mi/h}}\]
The speed is slightly over the limit.
A kilogram of mandarin costs 1.45 euros. Given the exchange rate of 1 euro = 1.18 dollars, how many lb of mandaring can you by with 5.00 dollars?
2.92 kg
This will be a two-step calculation where first, we convert the 5 dollars to euros and divide that by the price of mandarins. In dimensional analysis, there is no division, and we always multiply by choosing the correct conversion factor that cancels the unnecessary units.
\[{\rm{5}}{\rm{.00}}\,\cancel{{{\rm{dollars}}}}\,{\rm{ \times }}\,\frac{{{\rm{1}}\,\cancel{{{\rm{euro}}}}}}{{{\rm{1}}{\rm{.18}}\,\cancel{{{\rm{dollars}}}}}}\,{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{kg}}\,}}{{{\rm{1}}{\rm{.45}}\,\cancel{{{\rm{euro}}}}}}\;{\rm{ = }}\,{\rm{2}}{\rm{.92}}\,{\rm{kg}}\]
Density
A 20.0-mL sample of a liquid has a mass of 17.8 g. What is the liquid’s density in grams per milliliter?
0.89 g/mL
\[{\rm{d}}\;{\rm{ = }}\,\,\frac{{\rm{m}}}{{\rm{v}}}\,{\rm{ = }}\frac{{{\rm{17}}{\rm{.8}}\,{\rm{g}}}}{{{\rm{20}}{\rm{.0}}\,{\rm{mL}}}}\,{\rm{ = }}\;{\rm{0}}{\rm{.89}}\,{\rm{g/mL}}\]
A sample containing 31.25 g of metal pellets is poured into a graduated cylinder initially containing 11.9 mL of water, causing the water level in the cylinder to rise to 18.7 mL. Calculate the density of the metal.
4.60 g/mL
In these types of problems, you need to realize that the volume displaced by the metal pellets is the volume of the liquid. Therefore, we have the mass and the volume of the metal, and we can calculate the density:
\[{\rm{d}}\;{\rm{ = }}\,\,\frac{{\rm{m}}}{{\rm{v}}}\,{\rm{ = }}\frac{{{\rm{31}}{\rm{.25}}\,{\rm{g}}}}{{{\rm{(18}}{\rm{.7}}\;{\rm{ – }}\,{\rm{11}}{\rm{.9)}}\;{\rm{mL}}}}\,{\rm{ = }}\;{\rm{4}}{\rm{.60}}\,{\rm{g/mL}}\]
What is the mass of a 2.85 L sample of a liquid that has a density of 0.954 g/mL?
2.72 x 103 g
The first thing is to make sure the units in density match those of volume. It is not the case here, and we can convert the L to mL first:
\[{\rm{v}}\,{\rm{ = }}\;{\rm{2}}{\rm{.85}}\,\cancel{{\rm{L}}}\; \times \,\frac{{{\rm{1000}}\,{\rm{mL}}}}{{{\rm{1}}\;\cancel{{\rm{L}}}}}\,{\rm{ = }}\;{\rm{2850}}\;{\rm{mL}}\]
And now we can calculate the mass:
\[{\rm{m}}\;{\rm{ = }}\,{\rm{d}}\,{\rm{ \times }}\,{\rm{v}}\,{\rm{ = 0}}{\rm{.954}}\,\frac{{\rm{g}}}{{\cancel{{{\rm{mL}}}}}}\;{\rm{ \times }}\,{\rm{2850}}\,\cancel{{{\rm{mL}}}}\,{\rm{ = }}\;{\rm{2}}{\rm{.72}}\;{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{\rm{3}}}\;{\rm{g}}\]
What is the volume of 100. g bromine in milliliters if it has a density of 3.10 g/cm3?
32.3 g/cm3
\[{\rm{v}}\;{\rm{ = }}\,\frac{{\rm{m}}}{{\rm{d}}}\,{\rm{ = }}\,\frac{{{\rm{100}}{\rm{.}}\,{\rm{g}}}}{{{\rm{3}}{\rm{.10}}\,{\rm{c}}{{\rm{m}}^{\rm{3}}}}}\,{\rm{ = }}\;{\rm{32}}{\rm{.3}}\,{\rm{g/c}}{{\rm{m}}^{\rm{3}}}\]
Complete the missing data for the density, mass, and volume in the following table:
| Mass | Volume | Density |
| 2.35 g | 0.035 L | X g/mL |
| X lb | 356 mL | 1.56 g/cm3 |
| 14.6 kg | X gal | 4.81 g/mL |
Row 1 – 0.0671 g/mL
Row 2 – 1.22 lb
Row 3 – 0.802 gal
For all the questions, we need to pay attention to the units.
Row 1)
In the first step, we get the density in g/L, and the second multiplication converts L to mL.
\[{\rm{d}}\;{\rm{ = }}\,\,\frac{{\rm{m}}}{{\rm{v}}}\,{\rm{ = }}\frac{{{\rm{2}}{\rm{.35}}\,{\rm{g}}}}{{{\rm{0}}{\rm{.035}}\;\cancel{{\rm{L}}}}}\,{\rm{ \times }}\,\frac{{{\rm{1}}\,\cancel{{\rm{L}}}}}{{{\rm{1000}}\,{\rm{mL}}}}{\rm{ = }}\;{\rm{0}}{\rm{.0671}}\,{\rm{g/mL}}\]
Row 2) Remember that 1 cm3 = 1 mL, and therefore, we cancel them.
\[{\rm{m}}\;{\rm{ = }}\,{\rm{d}}\,{\rm{ \times }}\,{\rm{v}}\,{\rm{ = }}\,{\rm{1}}{\rm{.56}}\,\frac{{\cancel{{\rm{g}}}}}{{\cancel{{{\rm{c}}{{\rm{m}}^{\rm{3}}}}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{lb}}}}{{{\rm{453}}{\rm{.6}}\,\cancel{{\rm{g}}}}}\,{\rm{ \times }}\,{\rm{356}}\,\cancel{{{\rm{c}}{{\rm{m}}^{\rm{3}}}}}\,{\rm{ = }}\;{\rm{1}}{\rm{.22}}\;{\rm{lb}}\]
Row 3)
We can convert the units of m and d first, and then plug in the numbers in the formula of volume.
m = 14.6 kg x 1000 = 14600 g
\[{\rm{d}}\;{\rm{ = }}\,{\rm{4}}{\rm{.81}}\,\frac{{\rm{g}}}{{\cancel{{{\rm{mL}}}}}}\;{\rm{ \times }}\;\frac{{{\rm{1000}}\,\cancel{{{\rm{mL}}}}}}{{{\rm{1}}\,\cancel{{\rm{L}}}}}\,{\rm{ \times }}\,\frac{{{\rm{3}}{\rm{.786}}\,\cancel{{\rm{L}}}}}{{{\rm{1}}\,{\rm{gal}}}}{\rm{ = }}\;{\rm{18,211}}\,{\rm{g/gal}}\]
\[{\rm{v}}\;{\rm{ = }}\,\frac{{\rm{m}}}{{\rm{d}}}\,{\rm{ = }}\,\frac{{{\rm{14600}}\,{\rm{g}}}}{{{\rm{18211}}\,{\rm{g/gal}}}}\,{\rm{ = }}\;{\rm{0}}{\rm{.802 gal}}\]
How many kilograms of honey with a density of 1.40 kg/L are there in a gallon container?
5.30 kg
In the first part of the calculation, we convert the units of density to kg/gal, and the last multiplication is to determine the mass in kilograms.
\[{\rm{m}}\;{\rm{ = }}\,{\rm{d}}\,{\rm{ \times }}\,{\rm{v}}\,{\rm{ = }}\,{\rm{1}}{\rm{.40}}\,\frac{{{\rm{kg}}}}{{\cancel{{\rm{L}}}}}\;{\rm{ \times }}\,\frac{{{\rm{3}}{\rm{.786}}\,\cancel{{\rm{L}}}}}{{{\rm{1}}\,\cancel{{{\rm{gal}}}}}}\,{\rm{ \times }}\,{\rm{1}}\,\cancel{{{\rm{gal}}}}\,{\rm{ = }}\;{\rm{5}}{\rm{.30}}\;{\rm{kg}}\]
The density of iron is 8.96 g/cm3. What is its density in pounds per cubic inch (lb/in3)?
0.324 lb/in3
\[{\rm{8}}{\rm{.96}}\,\frac{{\cancel{{\rm{g}}}\,}}{{\cancel{{{\rm{c}}{{\rm{m}}^{\rm{3}}}}}}}\,{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{lb}}}}{{{\rm{453}}{\rm{.6}}\,\cancel{{\rm{g}}}}}{\rm{ \times }}\,\frac{{{\rm{(2}}{\rm{.54}}\,\cancel{{{\rm{cm}}{{\rm{)}}^{\rm{3}}}}}}}{{{{{\rm{(1}}\,{\rm{in)}}}^{\rm{3}}}}}\,{\rm{ = }}\,{\rm{0}}{\rm{.324}}\,{\rm{lb/i}}{{\rm{n}}^{\rm{3}}}\]
The density of iron is 7.86 g/cm3. What is the volume of 5.24 lb of iron expressed in cubic inches?
18.5 in3
The plan would be to convert the mass to grams and use it to calculate the volume which would be in cm3. Once we have this, we can convert it to in3.
\[{\rm{m}}\;{\rm{ = }}\,{\rm{5}}{\rm{.24}}\;\cancel{{{\rm{lb}}}}\,{\rm{ \times }}\;\frac{{{\rm{453}}{\rm{.6}}\,{\rm{g}}}}{{{\rm{1}}\,\cancel{{{\rm{lb}}}}}}\;{\rm{ = }}{\rm{2376}}{\rm{.9}}\,{\rm{g}}\]
\[{\rm{v}}\;{\rm{ = }}\,\frac{{\rm{m}}}{{\rm{d}}}\,{\rm{ = }}\,\frac{{{\rm{2376}}{\rm{.9}}\,{\rm{g}}}}{{{\rm{7}}{\rm{.86}}\,{\rm{g/c}}{{\rm{m}}^{\rm{3}}}}}\,{\rm{ = }}\;{\rm{302}}{\rm{.4 c}}{{\rm{m}}^{\rm{3}}}\]
\[{\rm{v}}\;{\rm{ = }}\,{\rm{302}}{\rm{.4 c}}{{\rm{m}}^{\rm{3}}}\,{\rm{ \times }}\,\frac{{{{\left( {{\rm{1}}\,{\rm{in}}} \right)}^{\rm{3}}}}}{{{{{\rm{(2}}{\rm{.54}}\,{\rm{cm)}}}^{\rm{3}}}}}\; = \;18.5\,{\rm{i}}{{\rm{n}}^{\rm{3}}}\]
A plastic cylinder has a length of 7.25 in, a radius of 1.26 in, and a mass of 841 g. What is the density of the plastic in g/cm3?
1.42 g/cm3
The volume of a cylinder is calculated by the formula v = π · r2 · l. We can either convert the length and radius to cm and determine the volume in cm3, or use the data given in inches, determine the volume in in3 and convert that into cm3.
Let’s go with the second option.
v = π · r2 · l = 3.14 x (1.26)2 in x 7.25 in = 36.1417 in3
Next, we convert the volume to cm3:
\[{\rm{v}}\;{\rm{ = }}\,{\rm{36}}{\rm{.1417 i}}{{\rm{n}}^{\rm{3}}}\,{\rm{ \times }}\,\frac{{{{{\rm{(2}}{\rm{.54}}\,{\rm{cm)}}}^{\rm{3}}}}}{{{{\left( {{\rm{1}}\,{\rm{in}}} \right)}^{\rm{3}}}}}\; = \;592.3\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\]
The last step is to determine the density:
\[{\rm{d}}\;{\rm{ = }}\,\,\frac{{\rm{m}}}{{\rm{v}}}\,{\rm{ = }}\frac{{{\rm{841}}\,{\rm{g}}}}{{{\rm{592}}{\rm{.3}}\;{\rm{c}}{{\rm{m}}^{\rm{3}}}}}\, = \,{\rm{1}}{\rm{.42}}\,{\rm{g/c}}{{\rm{m}}^{\rm{3}}}\]
What is the radius of a steel sphere that has a mass of 65.0 g and a density of 7.86 g/cm3?
1.25 cm
The key here is the formula for the sphere volume:
\[{\rm{v}}\;{\rm{ = }}\,\frac{{\rm{4}}}{{\rm{3}}}\;{\rm{\pi }}\,{{\rm{r}}^{\rm{3}}}\]
We can rearrange the equation to get an expression for r and the only missing value would be the volume of the sphere which we can calculate from the mass and the density.
\[{\rm{v}}\;{\rm{ = }}\,\frac{{\rm{m}}}{{\rm{d}}}\,{\rm{ = }}\,\frac{{{\rm{65}}\,{\rm{g}}}}{{{\rm{7}}{\rm{.86}}\,{\rm{g/c}}{{\rm{m}}^{\rm{3}}}}}\,{\rm{ = }}\;{\rm{8}}{\rm{.2697 c}}{{\rm{m}}^{\rm{3}}}\]
The expression for r would be:
\[\sqrt[{\rm{3}}]{{\frac{{{\rm{3v}}}}{{{\rm{4\pi }}}}\;{\rm{ = }}\;}}\sqrt[{\rm{3}}]{{\frac{{{\rm{3}}\,{\rm{ \times }}\;{\rm{8}}{\rm{.2697}}\,{\rm{c}}{{\rm{m}}^{\rm{3}}}}}{{{\rm{4}}\,{\rm{ \times }}\,{\rm{3}}{\rm{.14}}}}\;{\rm{ = }}\;}}{\rm{1}}{\rm{.25}}\,{\rm{cm}}\]