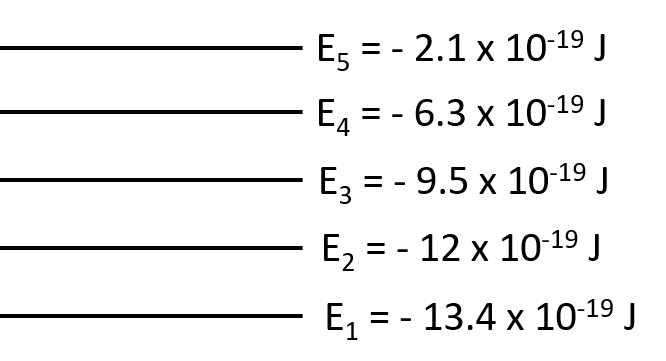Rydberg formula is used for calculating the wavelength or the energy of the light emitted during electron transitions.
So, first, what are the electron transitions, and how are they associated with light? The first thing you need to know here is the model suggested by Niels Bohr for the hydrogen atom.
This is shoer recap, but if you need to go over the details of this great theory that won a Nobel prize for Bohr, check the linked article here.
According to this model, the electron in the hydrogen atom circulates around the positively charged nucleus much like planets moving in orbits around the sun.
He postulated that each orbit has its own constant radius which is directly related to energy, and these energy levels are characterized by the principal quantum number (n) which is a whole number. Each energy level is represented as n1, n2, n3, and so on. The larger the radius, the higher energy, so n = 2 has greater energy than n = 1 and n = 3 has greater energy than n = 2, and so on.
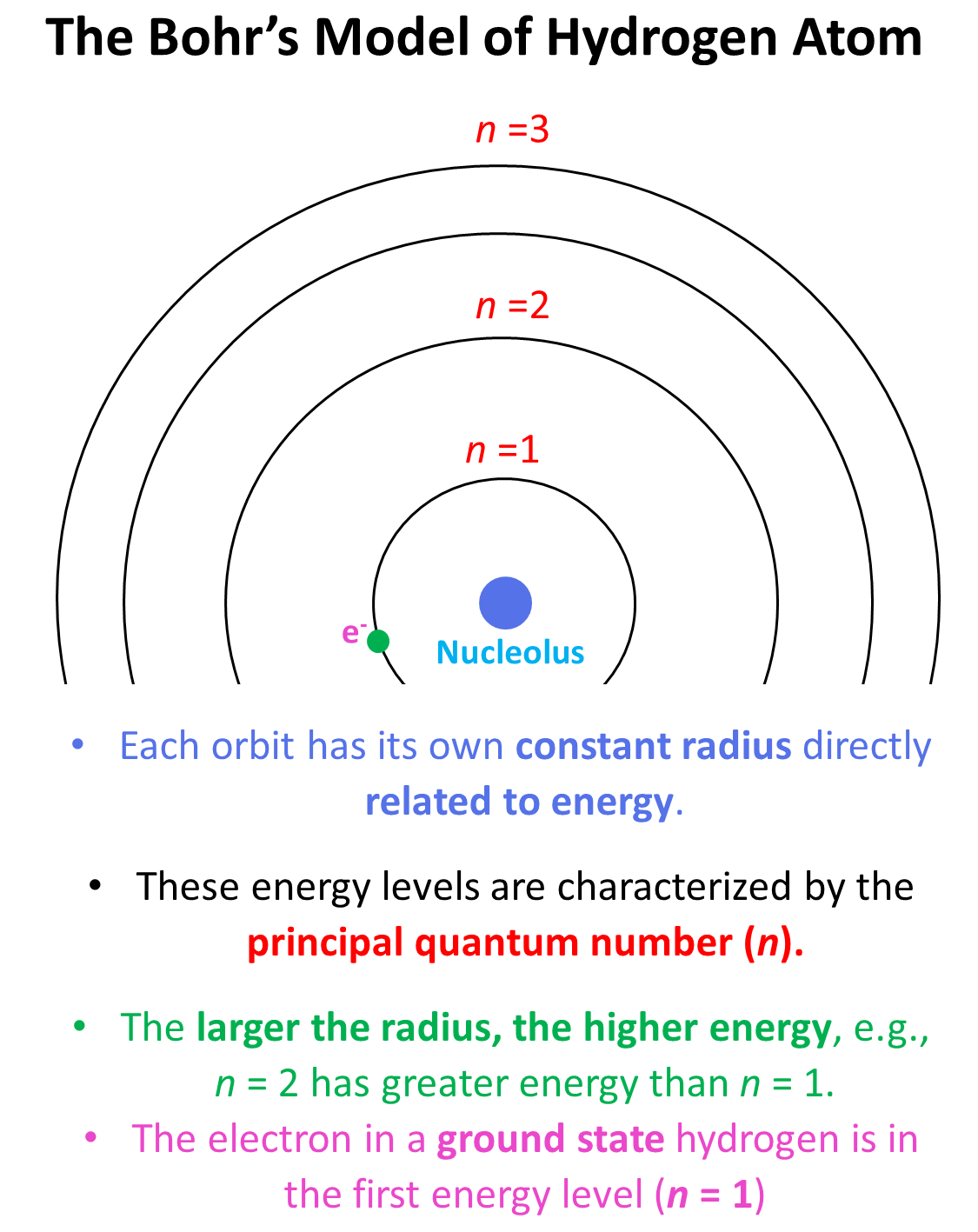
Generally, when the electron(s) is in the lowest possible energy level, the atom is said to be in the ground state, and when it is in a higher energy state, the atom is in an excited state. Importantly, the electron cannot randomly change orbits. To go into a higher energy level, it needs to absorb energy, and falling back into a lower energy level, it releases energy mainly in the form of light.
So, absorbing light with sufficient energy moves the electron to a higher energy level, and when it falls back to a lower energy level, light is emitted as energy is lost.
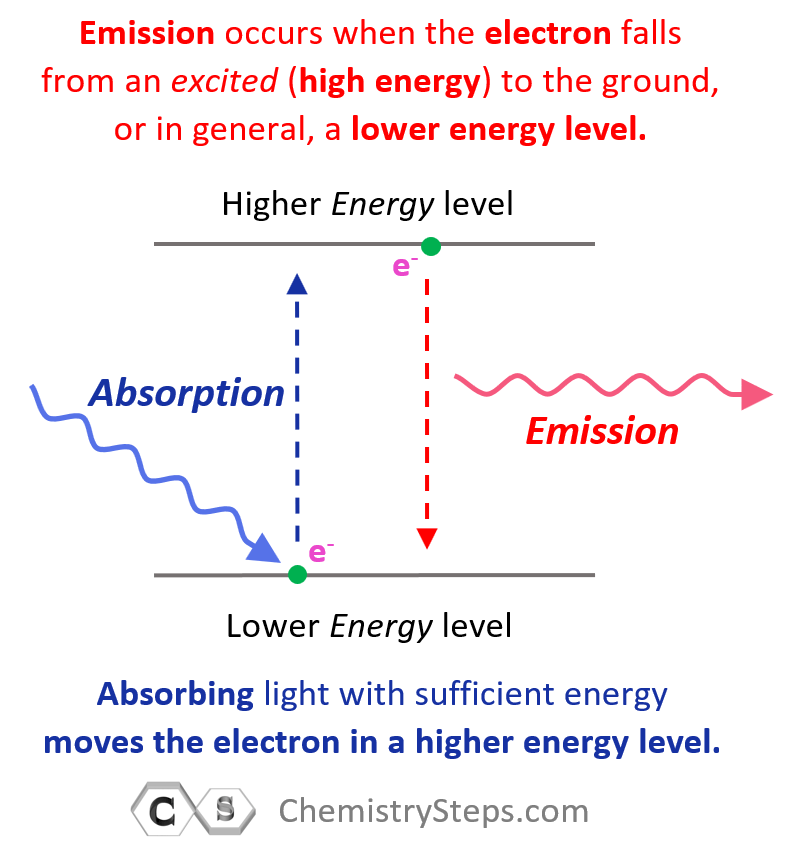
Each transition is characterized by specific (quantized) energy and therefore, photons (light) of specific colors are emitted. The greater the difference in energy levels, the higher energy (shorter wavelength) of the emitted light is.

And this was observed first by using a set consisting of a hydrogen lamp, where the electrons were excited by electric current, a narrow slit to pass a beam of light, and a prism that could separate all the wavelengths of the light emitted by hydrogen.
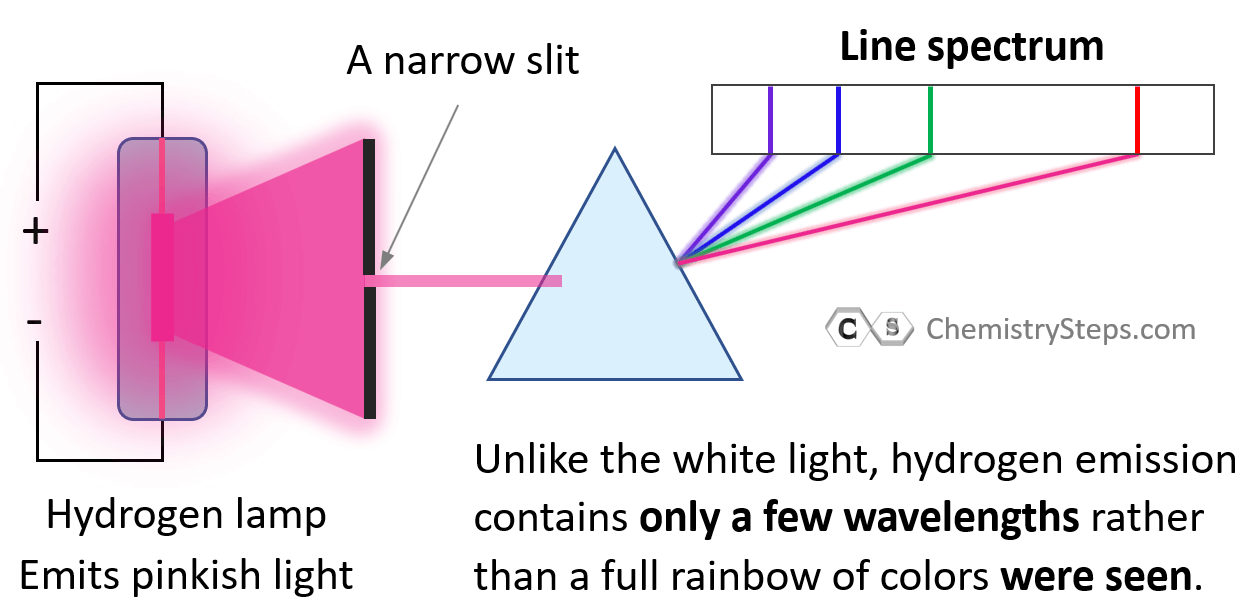
Notice again that only lines of specific few wavelengths rather than a full rainbow of colors were seen.
Calculating The Wavelength of Electron Transition
So, how do we calculate the wavelength of the light for electron transitions in the hydrogen atom? For this, Johann Balmer (1825–1898) and Johannes Rydberg (1854–1919) derived a formula correlating the wavelength of emitted photons for the given n levels.

This is the Balmer – Rydberg equation where m and n are the lower and higher energy orbits respectively, and R∞ (RH) is the Rydberg constant, which is equal to 1.097 x 10-2 nm-1.
For example, calculate the wavelength of light emitted by a hydrogen atom when electron moves from n = 5 → n = 2.
We can first write the Rydberg equation and rearrange it to get an expression for the wavelength:
\[\frac{1}{\lambda }\, = \,{R_\infty }\,\left( {\frac{1}{{{m^2}}}\; – \,\frac{1}{{{n^2}}}} \right)\]
\[\lambda \, = \,\frac{1}{{{R_\infty }\,\left( {\frac{1}{{{m^2}}}\; – \,\frac{1}{{{n^2}}}} \right)}}\,\]
And now, we can plug in the numbers:
\[\lambda \, = \,\frac{{\rm{1}}}{{{\rm{1}}{\rm{.097}}\,{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{ – 2}}}}{\rm{n}}{{\rm{m}}^{{\rm{ – 1}}}}\,\left( {\frac{{\rm{1}}}{{{{\rm{2}}^{\rm{2}}}}}\;{\rm{ – }}\,\frac{{\rm{1}}}{{{{\rm{5}}^{\rm{2}}}}}} \right)}}\,\]
\[\lambda \,{\rm{ = }}\,\frac{{\rm{1}}}{{{\rm{1}}{\rm{.097}}\,{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{ – 2}}}}{\rm{n}}{{\rm{m}}^{{\rm{ – 1}}}}\,\left( {\frac{{\rm{1}}}{{\rm{4}}}\;{\rm{ – }}\,\frac{{\rm{1}}}{{{\rm{25}}}}} \right)}}\;{\rm{ = }}\;{\rm{434}}\;{\rm{nm}}\,\]
We have seen in the picture above that this is one of the wavelengths in the Balmer series and corresponds to the emission of blue-violet light.
Calculating The Energy of Electron Transition
The Balmer – Rydberg equation was derived before the Bohr’s model for the hydrogen atom, and Bohr modified it to calculate the values of energy levels and their difference for the electron transitions. He substituted the λ with the corresponding expression based on the correlation of the wavelength and the speed of light which is given as:
\[E\; = \,{\rm{ – }}\,hc{R_\infty }\,\left( {\frac{1}{{{n^2}}}} \right)\; = \;{\rm{ – 2}}{\rm{.18}}\, \times \;{\rm{1}}{{\rm{0}}^{{\rm{ – 18}}}}\,{\rm{J}}\,\left( {\frac{1}{{{n^2}}}} \right)\]
Where h is the Planck’s constant (6.62 x 10-34 J · s), c is the speed of light (3 x 108 m/s), and RH is the Rydberg constant.
Their product gives a new constant expressed in Joules: 2.18 x 10– 18 J.
Notice that there is a negative sign in the formula, and it makes the energies of the electron negative for all values of n. This can be explained by considering that the energy of the electron in the atom is lower than the energy of a free electron.
So, this is for the energy of a given level. Now, how do we calculate the energy of the electron transition of the electron from one orbit (energy level)? It is calculated according to the difference in the energies of the two orbits:
ΔE = Efinal – Einitial = hν
Substituting the frequency (ν) with the corresponding expression for the λ in the Rydberg equation, we obtain a slightly modified Rydberg equation:
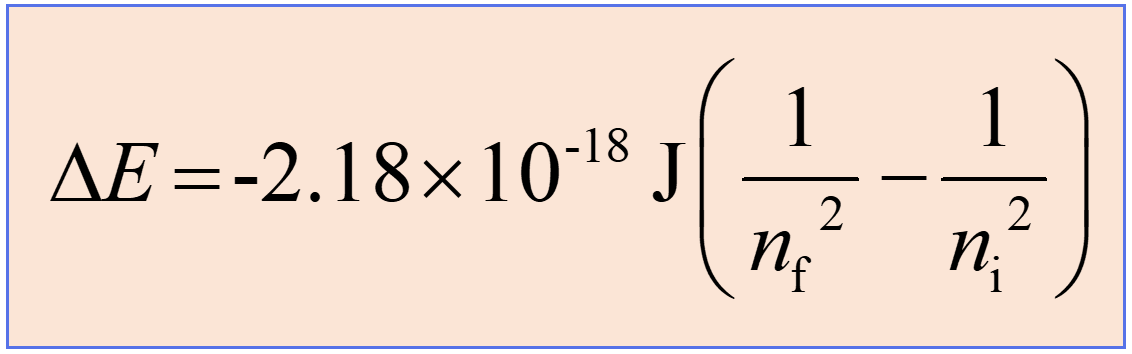
Now, if the electron moves from a lower to a higher energy state, then energy is absorbed, and subtracting 1/ni2 from 1/nf2 will allow canceling the negative signs, thus making ΔE positive. This is what we expect as the energy of the system increases (recall the endothermic and exothermic processes).
On the other hand, when the electron falls from a higher energy state, a photon is released, and the negative sign will stay making ΔE negative meaning the system loses energy. For example, when the electron moves from n = 2 to n = 1, we will have a positive ΔE:
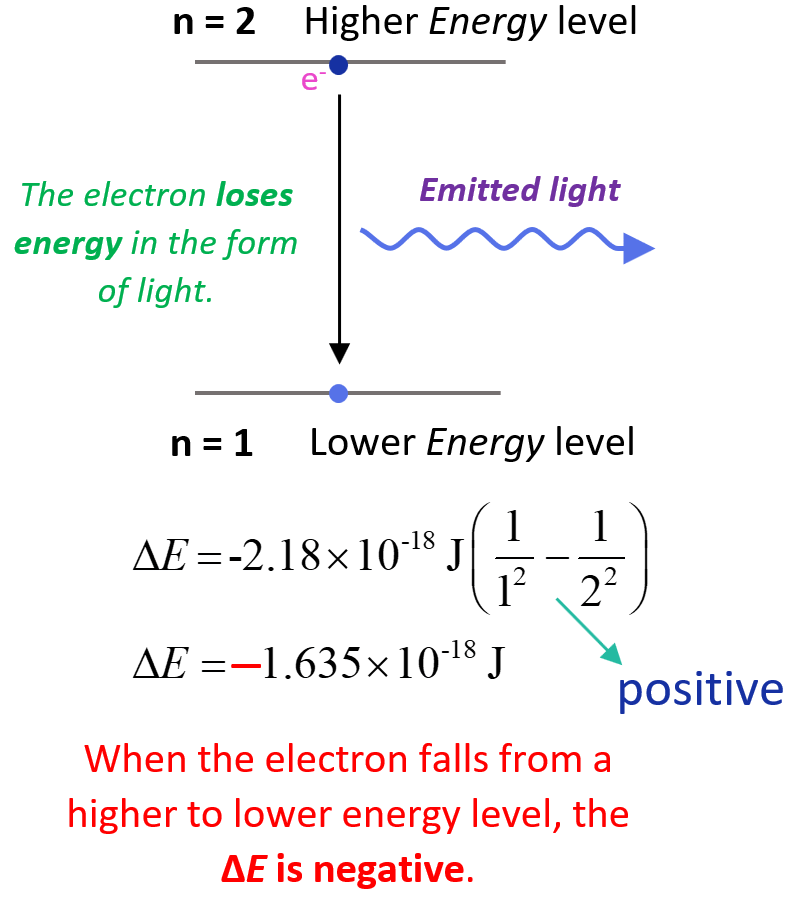
The lower (more negative) the energy is, the more stable the atom is. The energy is lowest (most negative) for n = 1. As n gets larger, the energy becomes less negative and therefore increases.
Let’s work on an example of determining the energy of electron transition in the hydrogen atom. Calculate the energy, in Joules, required to excite the electron from n = 1 to n = 3 level in a hydrogen atom.
\[\Delta E\, = \,{\rm{ – 2}}{\rm{.18}}\, \times \;{\rm{1}}{{\rm{0}}^{{\rm{ – 18}}}}\,{\rm{J}}\,\left( {\frac{1}{{{n_{\rm{f}}}^2}}\; – \,\frac{1}{{{n_{\rm{i}}}^2}}} \right)\]
ni = 1, nf = 3, and therefore, we can write:
\[{\rm{\Delta E}}\,{\rm{ = }}\,{\rm{ – 2}}{\rm{.18}}\,{\rm{ \times }}\;{\rm{1}}{{\rm{0}}^{{\rm{ – 18}}}}\,{\rm{J}}\,\left( {\frac{{\rm{1}}}{{{{\rm{3}}^{\rm{2}}}}}\;{\rm{ – }}\,\frac{{\rm{1}}}{{{{\rm{1}}^{\rm{2}}}}}} \right)\;{\rm{ = }}\;{\rm{1}}{\rm{.93}}\,{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{ – 18}}}}\,{\rm{J}}\]
The energy change is positive and therefore, it is absorbed by the system which is what is expected when the electron goes from a lower energy level (in this case ground state as n = 1) to a higher energy level (excited state).
Check this 95-question, Multiple-Choice Quiz on the Electronic Structure of Atoms including questions on properties of light such as wavelength, frequency, energy, quantum numbers, atomic orbitals, electron configurations, and more.
Check Also
- Atomic Orbitals
- Electron Configurations
- Electron Configurations of Ions
- Orbital Diagrams
- Aufbau’s Principle, Hund’s Rule, and Pauli’s Exclusion Principle
- Hund’s Rule
- Pauli Exclusion Principle
- Quantum Numbers (n, l, ml, ms)
- Bohr Model of the Hydrogen Atom
- The Photoelectric Effect
- Calculating The Energy of a Photon
- Effective Nuclear Charge
- Atomic Radius
- Ionic Radius
- Ionization Energy
- Electron Affinity
- Energy, Wavelength, and Frequency Practice Problems
- Electronic Structure of Atoms Quiz
- Periodic Table and Periodic Trends
Practice
Some electron transitions are shown below on a Bohr-model representation of the H atom.
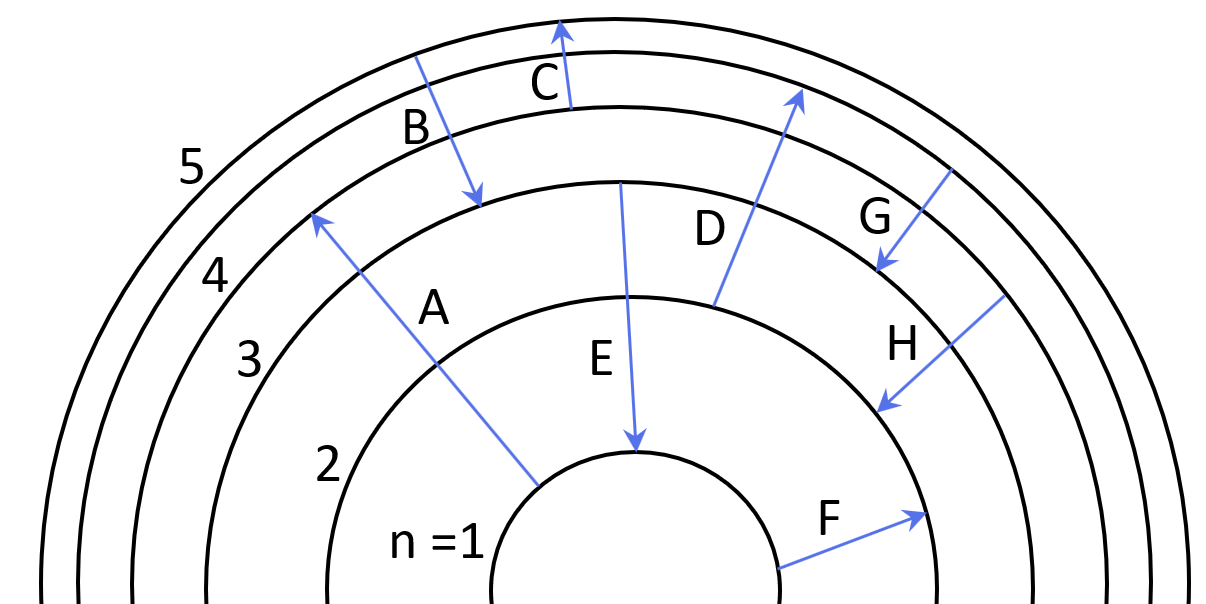
(a) Classify each transition as absorption or emission.
(b) Arrange the absorptions in terms of increasing energy.
(c) Rank the emissions in terms of decreasing wavelength of light.
For each of the following transitions, use the Rydberg equation to calculate the wavelength of light emitted by a hydrogen atom:
a) n = 3 → n = 2
b) n = 4 → n = 1
c) n = 6 → n = 3
What is the maximum wavelength of a photon that can excite the electron from n = 1 to n = 3 level in a hydrogen atom?
What is the energy level that the electron moves when a hydrogen atom at ground state absorbs a photon of wavelength 95 nm?
Would a photon of 115 nm light have sufficient energy to excite an electron in a ground state hydrogen atom to the n = 4 energy state?
What is the wavelength of the photon needed to excite an electron from the E1 to E4 level for a hypothetical atom given the following energy levels: