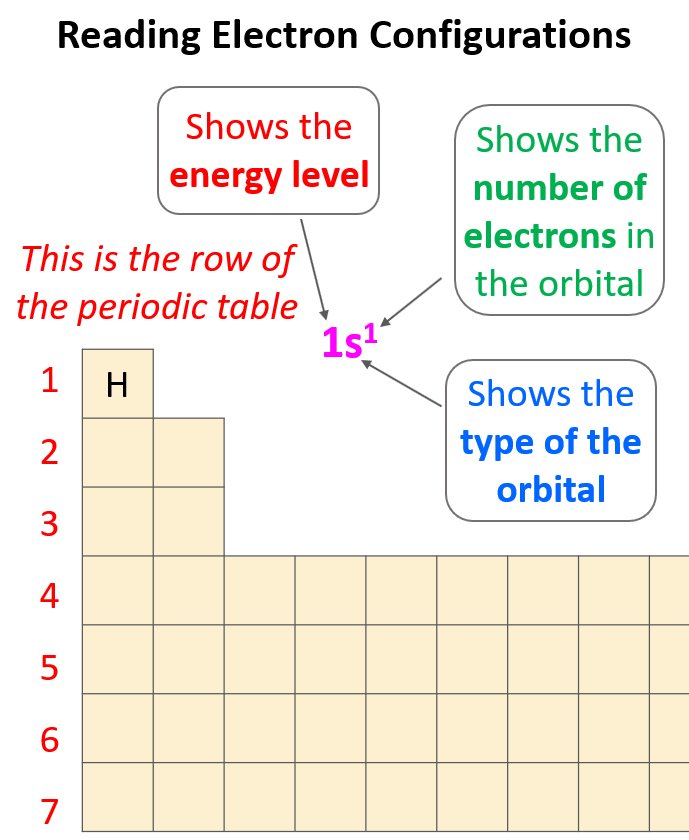
Electron configurations tell us the number and location of electrons in an atom or an ion. Let’s first write a simple electron configuration and see what each letter and number indicate. For example, hydrogen has an electron configuration of 1s¹. So, what do the letter, and the numbers tell us?

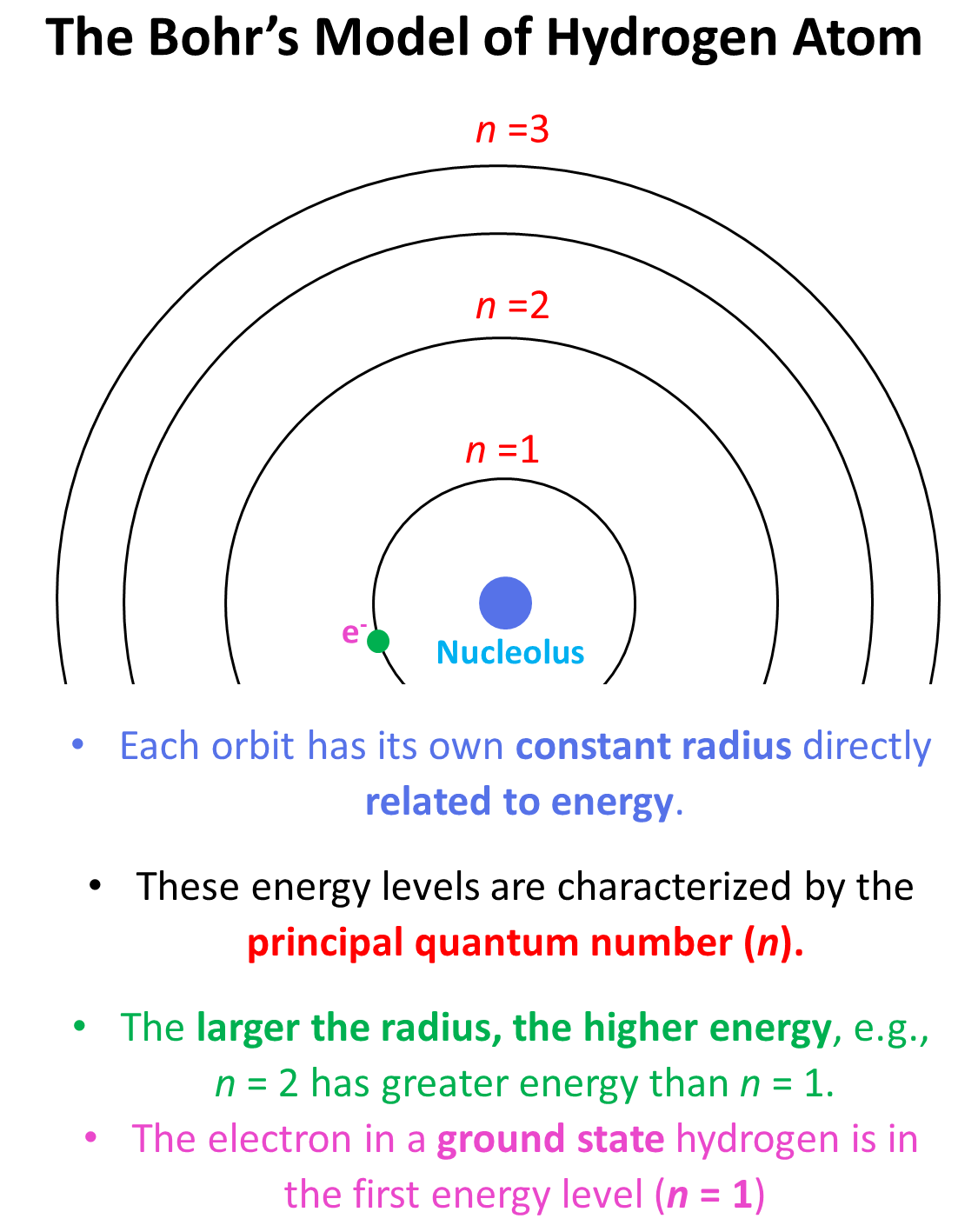
The first number in front of the “s” indicates the main energy level, and this is the principal quantum number, n. Remember, what we discussed about the Bohr model of the hydrogen atom. There are orbits with fixed radii each associated with discrete energy, and this is described by the principal quantum number n.

Next, we have the letter “s”, and this is the type of the orbital that the electron(s) is, and this is the energy sublevel because, for example, s and p orbitals in the same level have different energies. The number 1 given in the exponent tells us how many electrons we have in the s orbital that is in the first energy level:

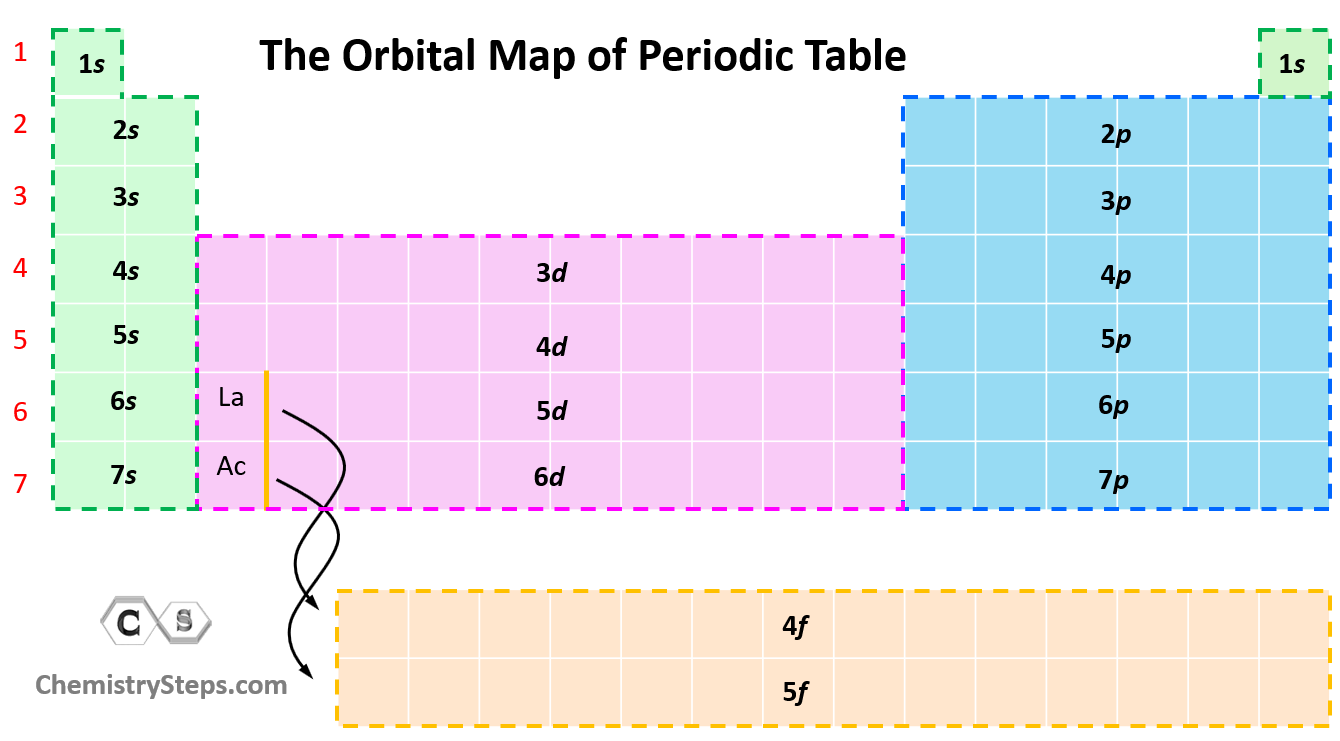
So, the number before each letter (except for the d and f orbitals that we will get to) can easily be determined based on the period of the periodic table where the element is located.

Let’s confirm this by looking at the electron configuration of fluorine: 1s²2s²2p⁵.

The 1s² means there are 2 electrons in the s orbital that is in the first row. Next, we have the orbitals in the second energy level because fluorine is in the second row of the periodic table. In this level, there are 2 electrons in an s orbital, and 5 electrons in the p orbital:

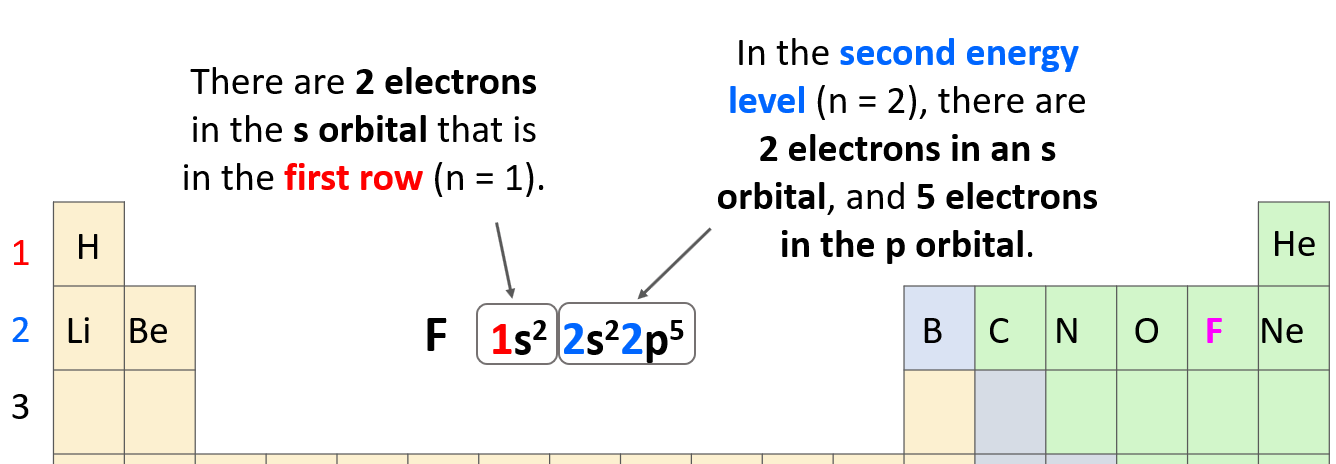
The total number of electrons must be equal to the atomic number of the element because remember, the atomic number shows the number of protons which, for a neutral atom, is equal to the number of electrons. The atomic number of fluorine is 9, and if we sum all the electrons in the configuration, we should get that number (2 + 2 + 5 = 9).

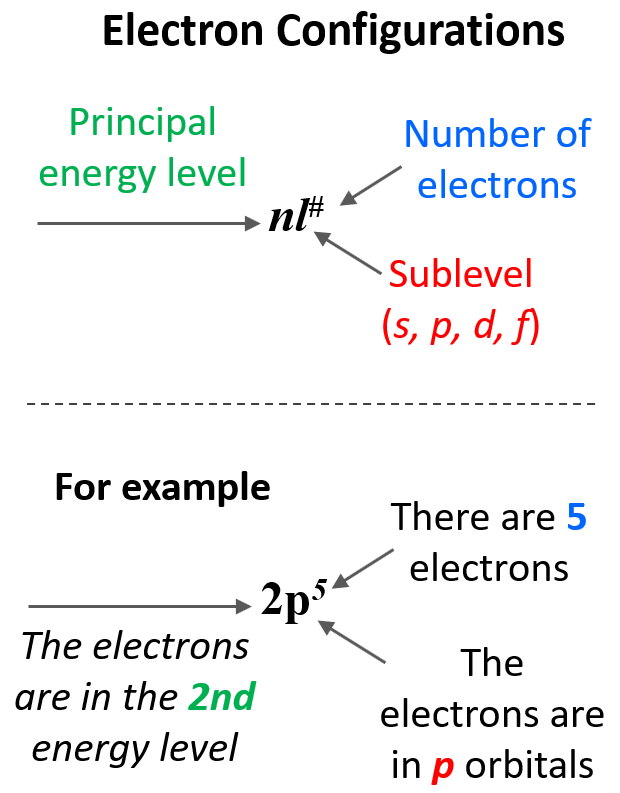
To summarize, we can see that the electron configuration shows first the principal energy level (n value), then the energy sublevel (l value – this is the type of the orbital i.e., s, p, d or f), and the number of electrons in this sublevel given as superscript:

Orbital Characteristics and Orbital Diagrams

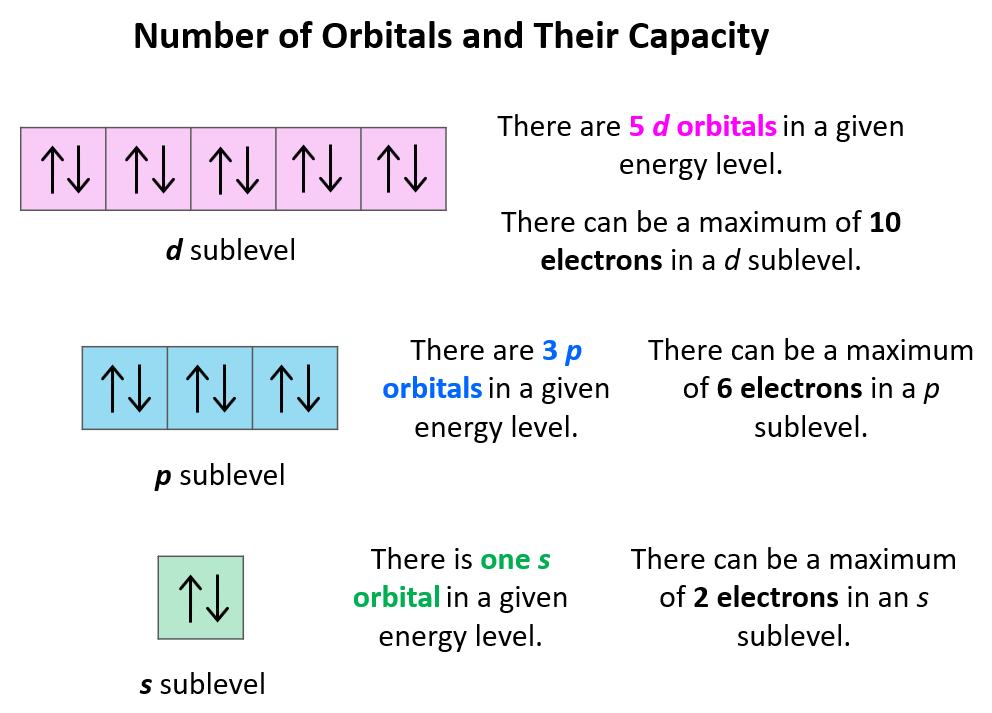
Now, a few important things about the orbitals and their electron capacity. First, remember that each orbital, whether it is s, p, d, or f can accommodate two electrons at most. So, you can never write things like 2s³ or 3p⁷, etc. The reason for 3p⁷ being wrong is that there are only 3 p orbitals in each energy level and because each can only take two electrons, the maximum number of electrons in the p sublevel is six. The orbitals are often shown as squares with electrons in them represented as arrows. These are called orbital diagrams:

If there are two electrons in the orbitals, the arrows must be shown in opposite directions which indicates that they must have opposite spins. This is according to the Pauli exclusion principle which states that no two electrons in an atom can have the same four quantum numbers. So, if the electrons are in the same orbital, they must have the same n, l, m_l, and therefore, the only one that can be different is the m_s which is the spin of the electron shown by the position of the arrow.

Next, remember the number and capacity of s, p, d, and f are energy sublevels There can only be 1 s orbital in the given energy level, 3 p orbitals, 5 d orbitals, and 7 f orbitals. And because each orbital can only take a maximum of two electrons, there can only be a maximum of two electrons in any s sublevel, 6 electrons in the p subshell, 10 in the d, and 14 in the f sublevel.

The next question we want to address is how to easily recognize what orbitals a given element has. For this, try to memorize this orbital map of the periodic table:

Rules of the Aufbau Principle

Aufbau (German aufbauen, “to build up”) principle tells us that electrons fill the orbitals in the order of increasing their energy level. An easy example illustrating the idea behind the aufbau principle would be pouring water into a tube structure with chambers at different height levels:

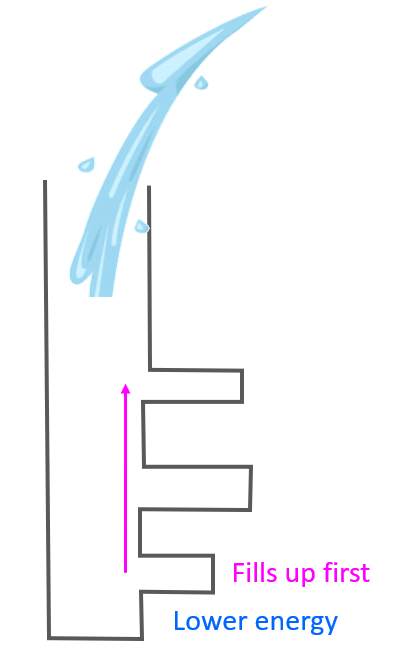
It is clear that the water is going to fill first the chambers in lower levels before starting to go into the ones at a higher level. We can explain this in terms of gravity, and potential energy as the chambers in lower levels have lower energy levels and therefore, the water in them would have lower potential energy which means higher stability. Remember, any system always tends to move towards a lower energy state.

The energy levels of the orbitals can be shown as follows:

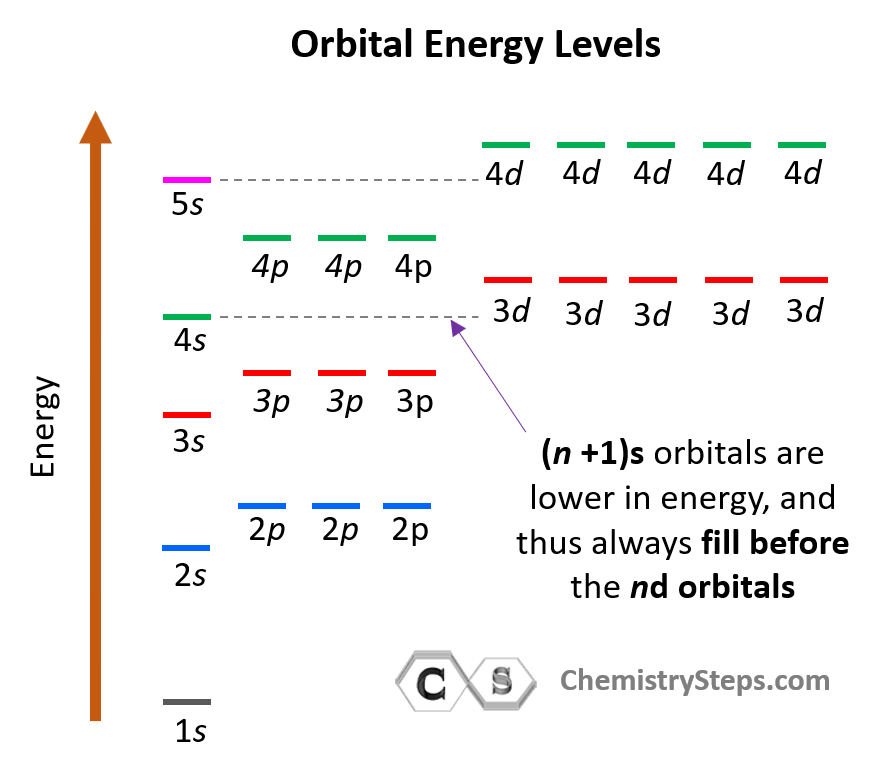
Notice that within the same principal level, orbitals with a lower value of l have lower energy (E) and therefore, are filled first. So, for a given value of n:

E (s orbital) < E ( p orbital) < E (d orbital) < E ( f orbital)

Now, in the periodic table, it may look a little different as the orbitals with lower energy levels are generally in the higher-standing rows. This is because remember, the rows (periods) of the periodic table indicate the principal quantum number (n), which is the energy level, and they increase as we go down the periodic table:

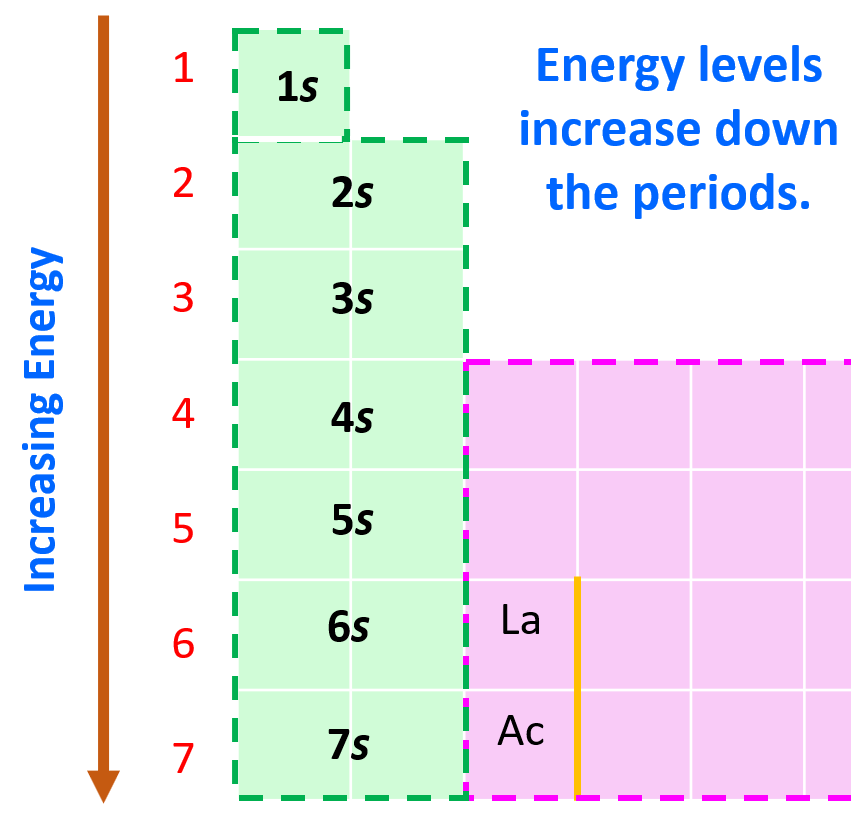
Considering this, and bringing back the analogy of water filling the chambers, you can visualize this pattern for filling the orbitals:

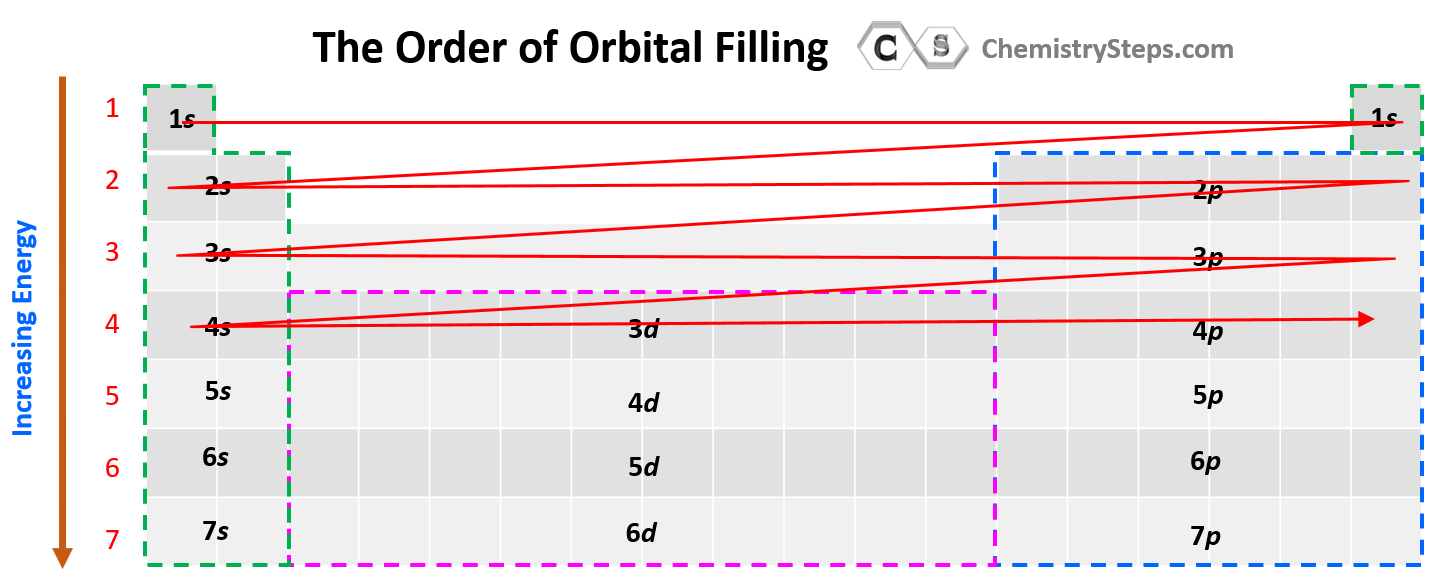
The water (electrons) fills first the s level, then the p, then the d, and the f subshells of the given energy level. There are some deviations when it comes to the d and f orbitals, and we will discuss that later in the article.

Let’s now do some more examples. First is the hydrogen, and it is in the first row, therefore, the only electron it has is going to be in the 1s level, and the electron configuration will be 1s¹:

For the He, it will be 1s² because it has two electrons, and the s orbital can still accommodate one more electron.

Next, we have lithium. Now, it is in the second row, but before getting there, we must use the 1s orbital. Remember, water couldn’t jump up without filling the lower levels. So, lithium has 3 electrons (atomic number), and therefore, the electron configuration will be 1s²2s¹.

Consequently, Be will have one more electron with a configuration of 1s²2s².

Next, we have boron, and it is in the region of p orbitals. Therefore, everything we had for Be, is still going to be in place, and the one additional electron will go to the 2p orbital:

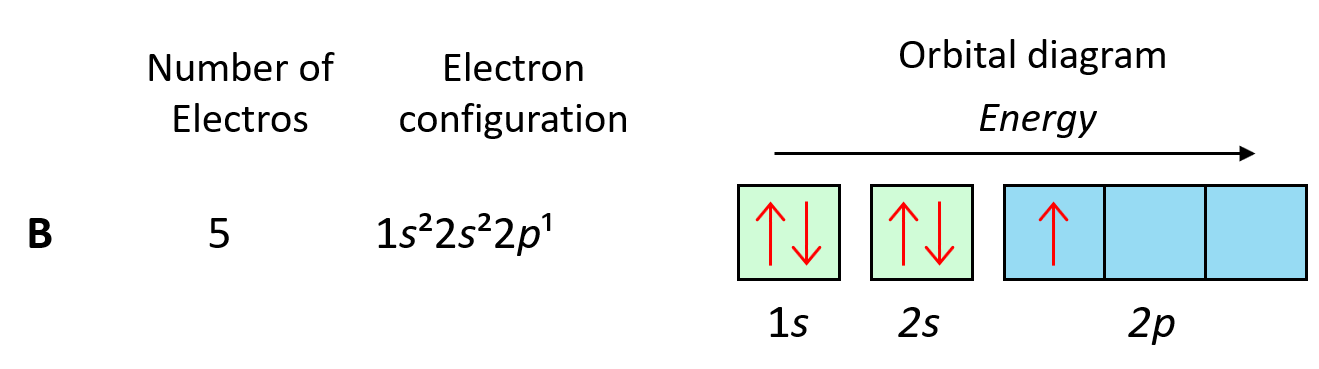
Now, carbon is going to add one more electron in the p sublevel thus having 1s²2s²2p² electron configuration. What is important is that this electron goes to the next (empty) p orbital rather than fitting in with the other electron:

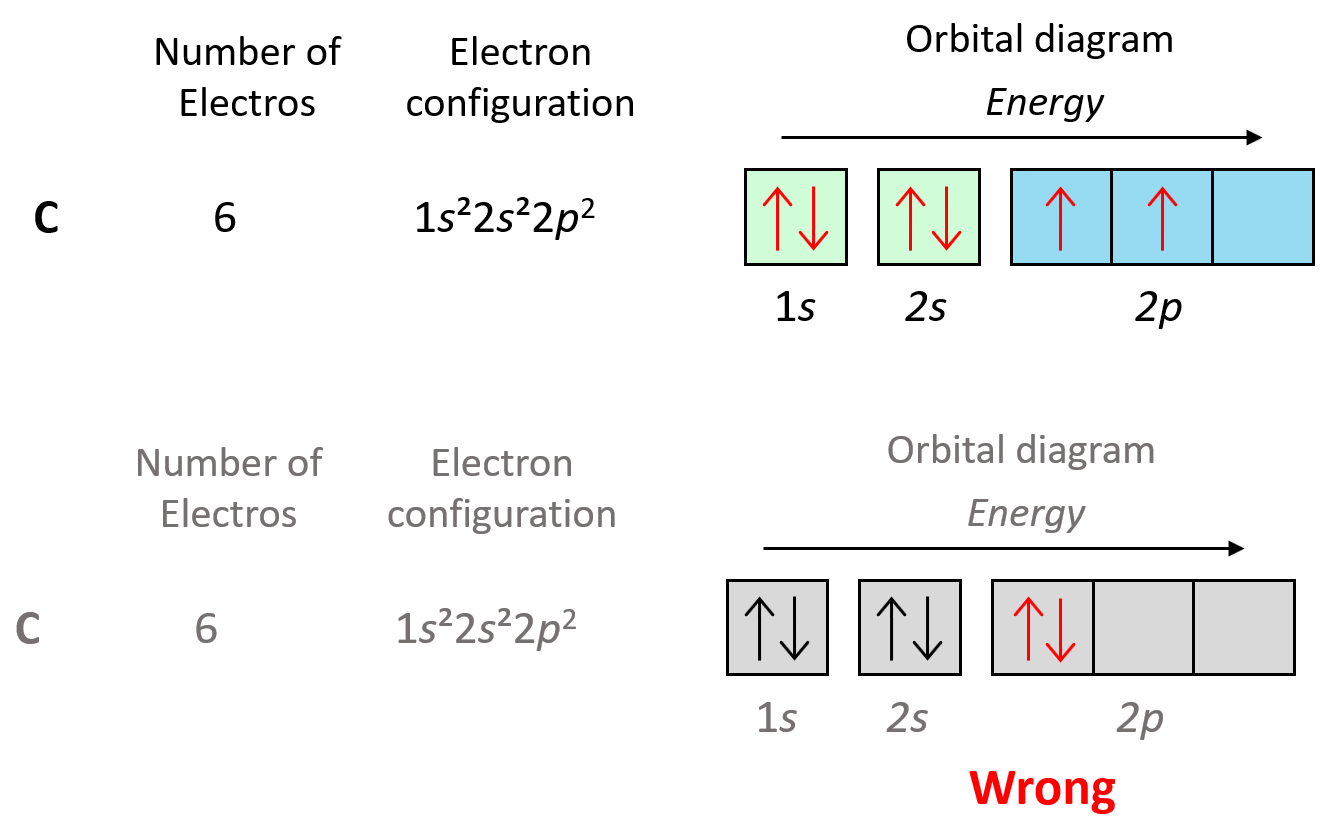
This is the Hund’s rule, which states that electrons will fill all the degenerate orbitals (equal in energy) with parallel spins (both arrows up or down) first before pairing up in one orbital. We can also formulate it as the lowest energy configuration for an atom is the one having the maximum number of unpaired electrons within the same energy sublevel.

Hund’s rule is another demonstration of the same principle which is the tendency to adopt the lowest energy state possible. There is a stronger repulsive interaction between two electrons in the same orbital compared to when they occupy separate orbitals of equal energy.

So, as expected, the next element, nitrogen will place the additional electron in the 3^rd p orbital which is empty in carbon.

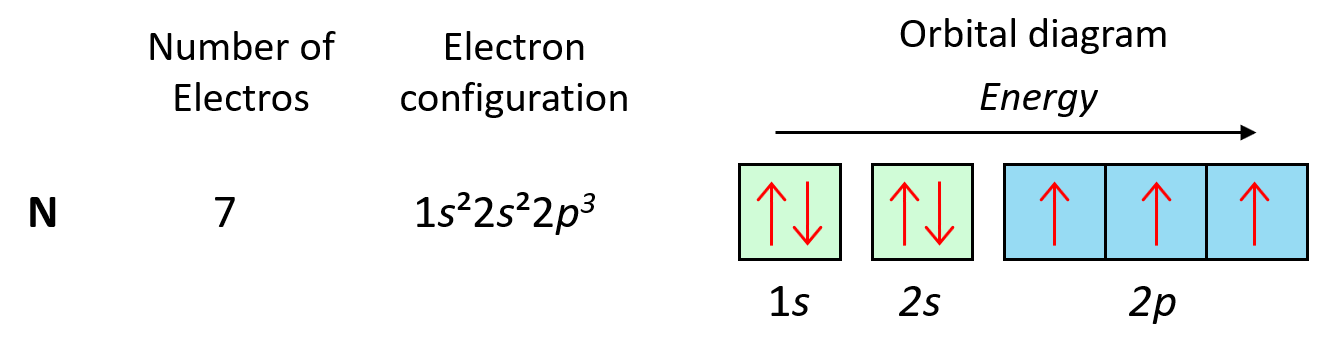
Following the same principle, we get to Ne which has a complete filling of the n = 2 principal level.

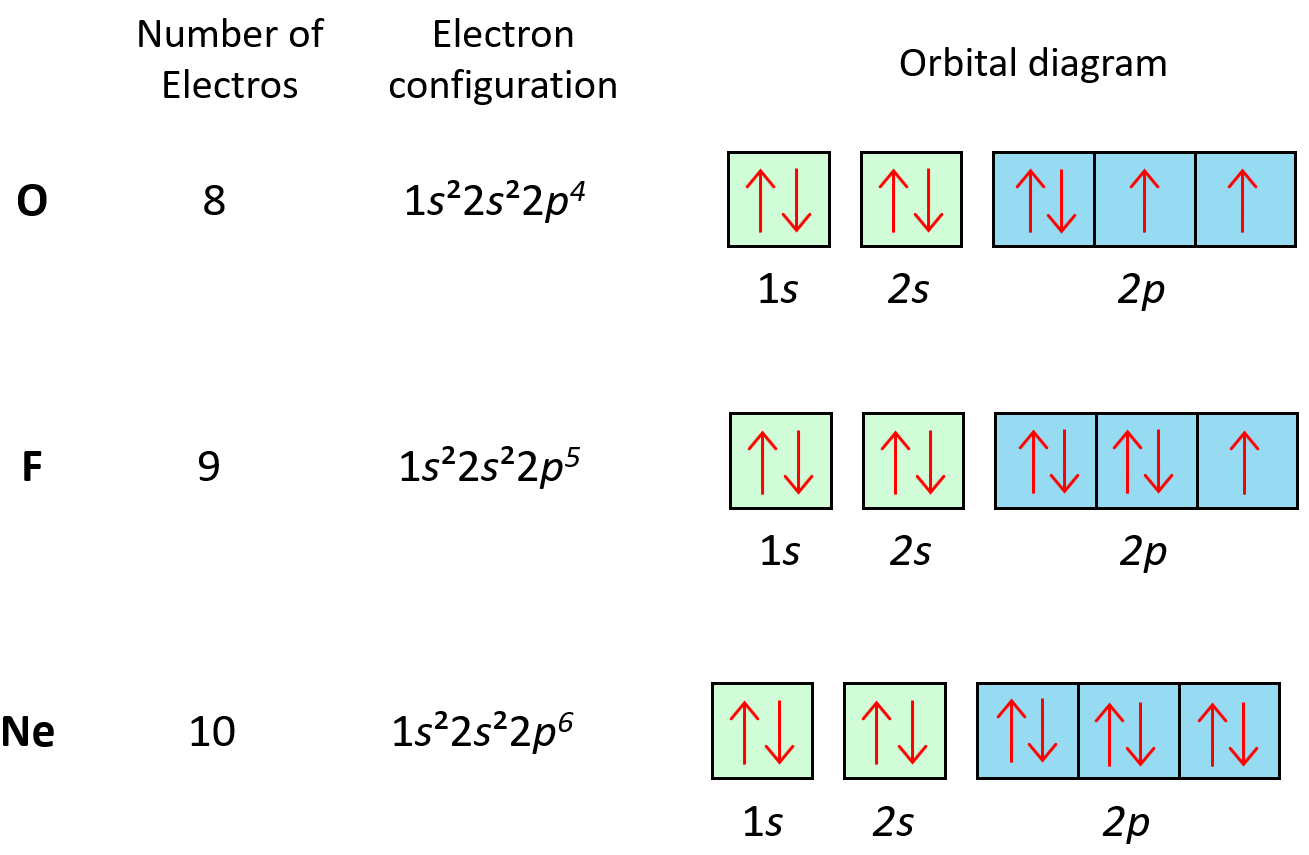
Now, there is something special about (completely) filled orbitals. This makes the electrons very low in energy meaning they are stable and cannot normally lower their energy more by participating in chemical reactions. Therefore, Ne and all the other noble gases below it, are the most chemically stable and thus unreactive (inert) family in the periodic table.

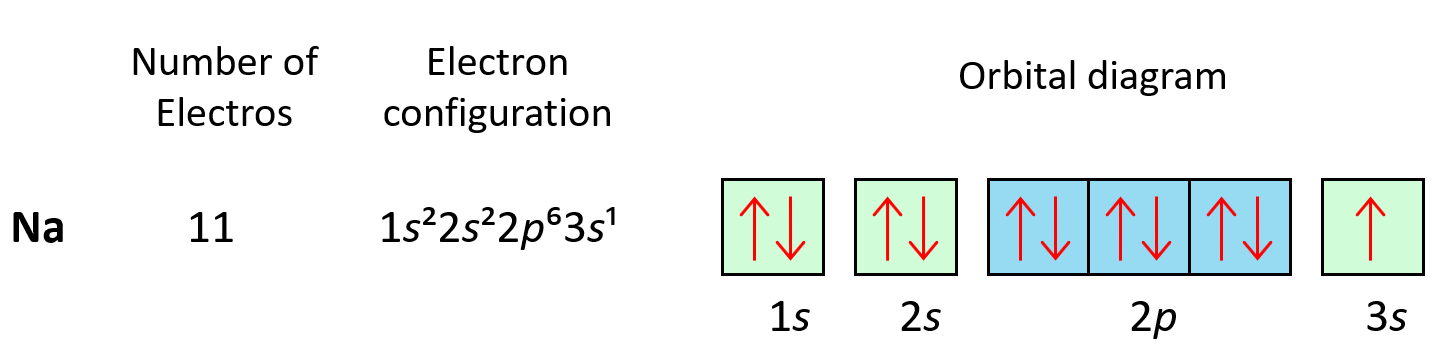
The first element in period 3 is sodium, Na, and we are going to write the electron configuration of Ne with an additional electron in the 3s sublevel:

Writing an Electron Configuration for an Element from Its Position in the Periodic Table 

At some point, when start noticing the pattern of filling the orbitals, and their mapping on the periodic table, it may be easier to write the electron configuration simply based on the position of the element. So, instead of starting from 1s²…., we write the electron configuration of the last noble gas that comes before the element and then add the remaining electrons from the corresponding n level. For example, let’s say we want to write an electron configuration for sulfur. First, you need to write the inner electron configuration, that is the configuration of the noble gas that precedes it in the periodic table. In this case, it is Ne, and since it is in the last element in the second row, the last filled sublevel would be 2p⁶, and therefore,  the electron configuration of the noble gas will be 1s²2s²2p⁶. Now, to this, we add 2 s electrons, and four p electrons since S is the fourth element in the p orbital area:

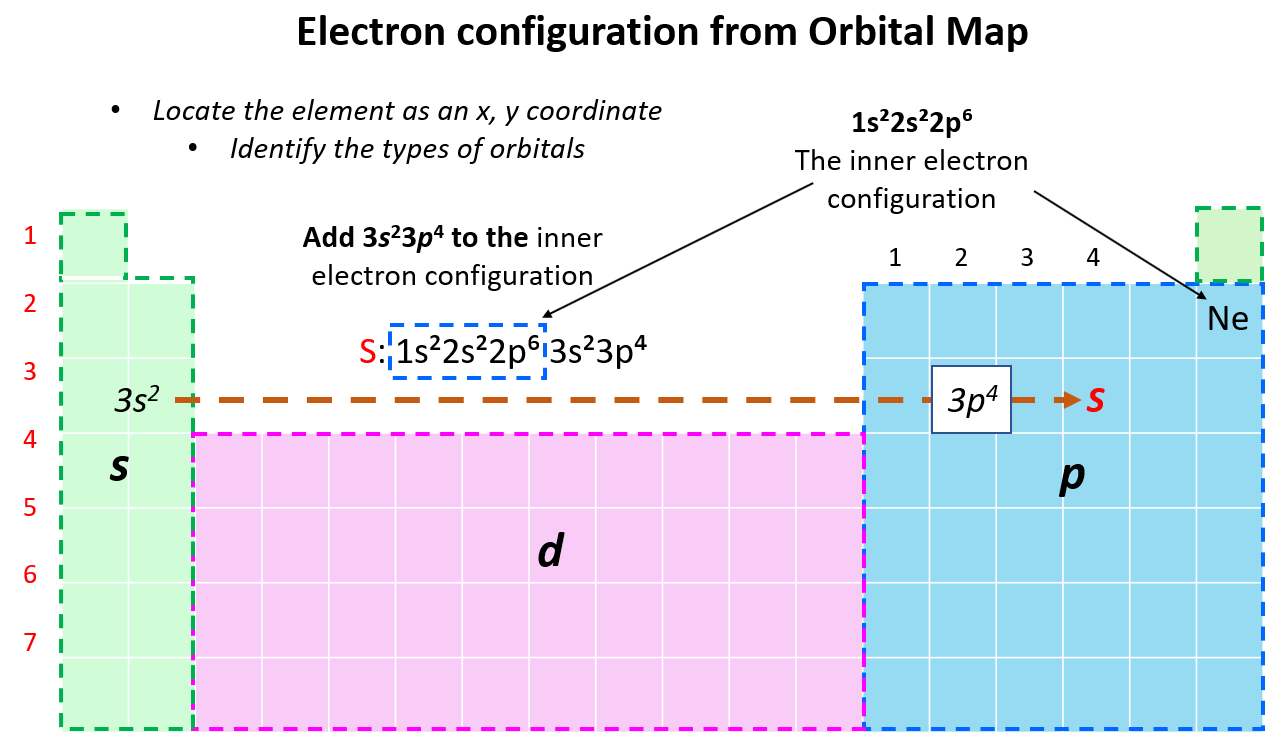
Therefore, the electron configuration will be 1s²2s²2p⁶3s²2p⁴.

Condensed electron configurations

In condensed electron configurations, we show the symbol of the noble gas that precedes the element in square brackets, and then add the remaining electrons just as we have been doing so far. So, for the sulfur, it will be S: [Ne]3s²2p⁴.

Another example is the electron configuration of Br. Since it is in the 4^th row, the inner configuration would be that of Ar, and after that, we add the electrons as we did for the d elements that we have discussed. Two electrons will go into the 4s orbital, 10 to the 3d orbitals, and 5 into the 4p sublevel – Br: [Ar]4s²3d¹⁰4p⁵.

Electron Configuration of d Elements – the Transition Series

There is one exception to keep in mind for the electron configuration of transition metals. That is the (n +1)s orbitals always fill before the nd orbitals.

For example, the 4s level fills before the 3d level, and therefore, the electron configuration of Ti is 1s^²2s^²2p^⁶3s^²3p^⁶4s^²3d^² or, the condensed configuration which will be [Ar]4s^²3d^².

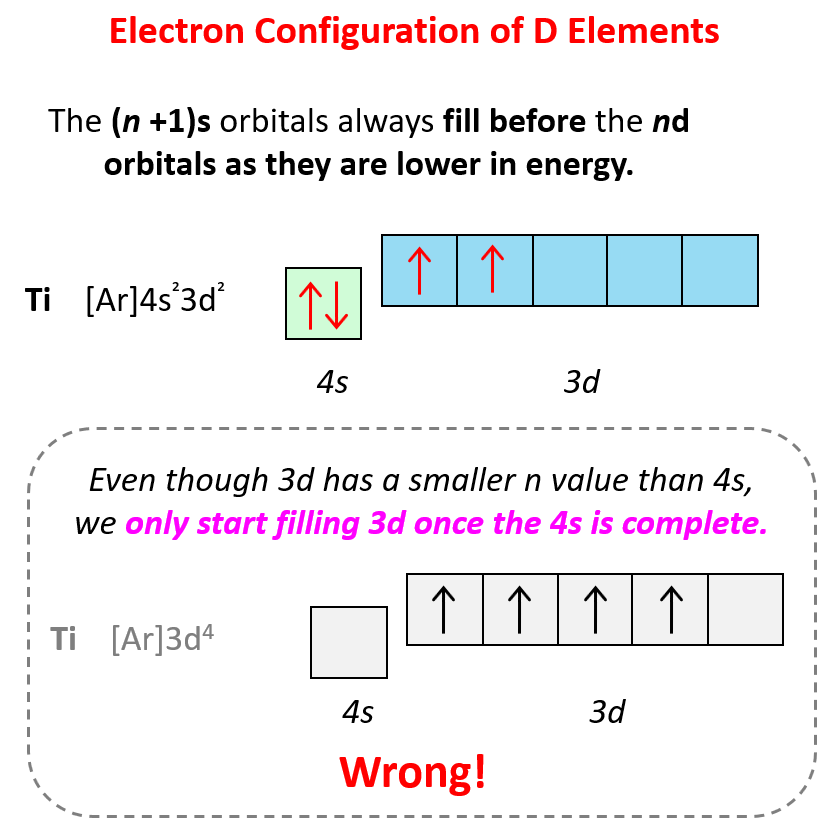
As we get to higher values of n, other variations in the filling pattern occur because the energy sublevels become very close together (recall the figure on the energy levels above).

Stability of Half-Filled and Filled Sublevels

We mentioned that noble gases are characterized by great stability because of their completely filled orbitals. Now, similar to this, orbitals tend to get lower energy levels (high stability) when they are half-filled. For example, following what we have learned so far, we may expect the following electron configuration for Cr: [Ar]4s^²3d⁴.

However, the electron configuration of Cr is [Ar]4s¹3d⁵, and the reason for this is that the d orbital gets a half-filled configuration (remember d orbitals can have a maximum of 10 electrons). We can think of this as the electron jumping from the 4s level to the 3d level and compensating this energy uphill by a stabilization associated with half-filled orbitals:

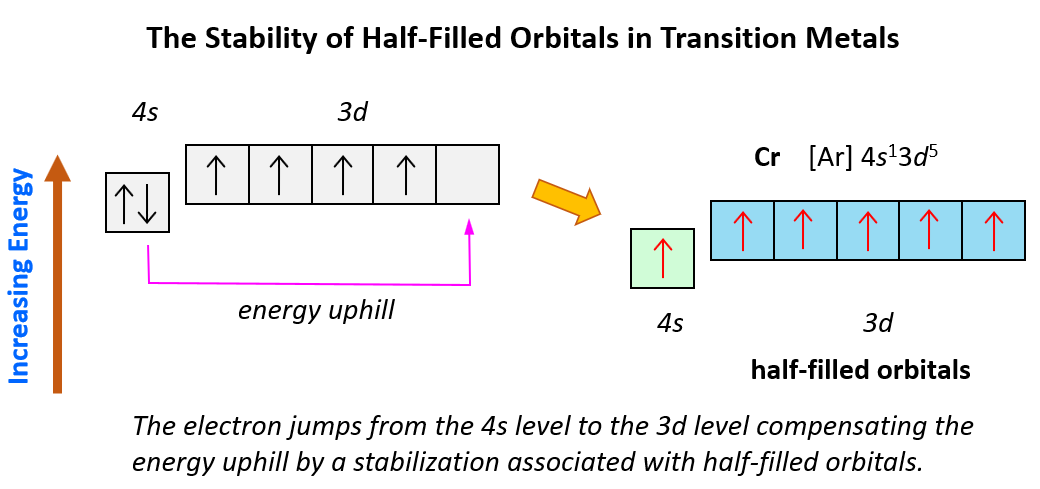
Of course, in reality, it is not as though the electrons fill one by one, and then one of them jumps from 4s to 3d level. However, this is a visual representation to help better understand this behavior in the electron configuration of transition elements.

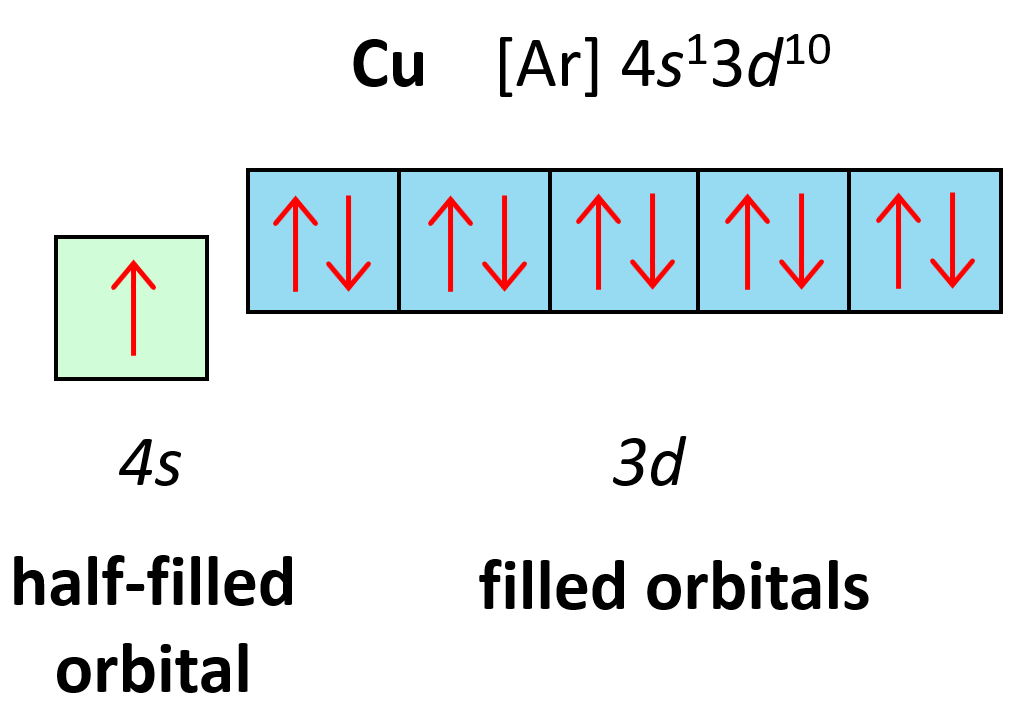
Let’s also discuss the electron configuration of Cu which stands before Zn, and one may expect it to have 9 electrons in the d sublevel. However, the correct electron configuration of Cu is [Ar]4s¹3d¹⁰ as this allows to attain filled d orbitals and a half-filled s orbital which is lower in energy (more stable) than the expected [Ar]4s²3d⁹ configuration.

Inner Transition Series (f Elements)

Starting from period 6, we have the inner transition elements which contain f orbitals. The first thing you need to remember here is that there are seven f orbitals because l = 3, so the possible ml values are −3, −2, −1, 0, +1, +2, and +3. Each orbital can accommodate two electrons and therefore, a total of 14 electrons can fill the given f sublevel.

Although the first element in this region is La, the filling of f orbitals starts from Cerium (Ce), and the elements together with it in the Period 6 are called lanthanides (or rare earth elements).

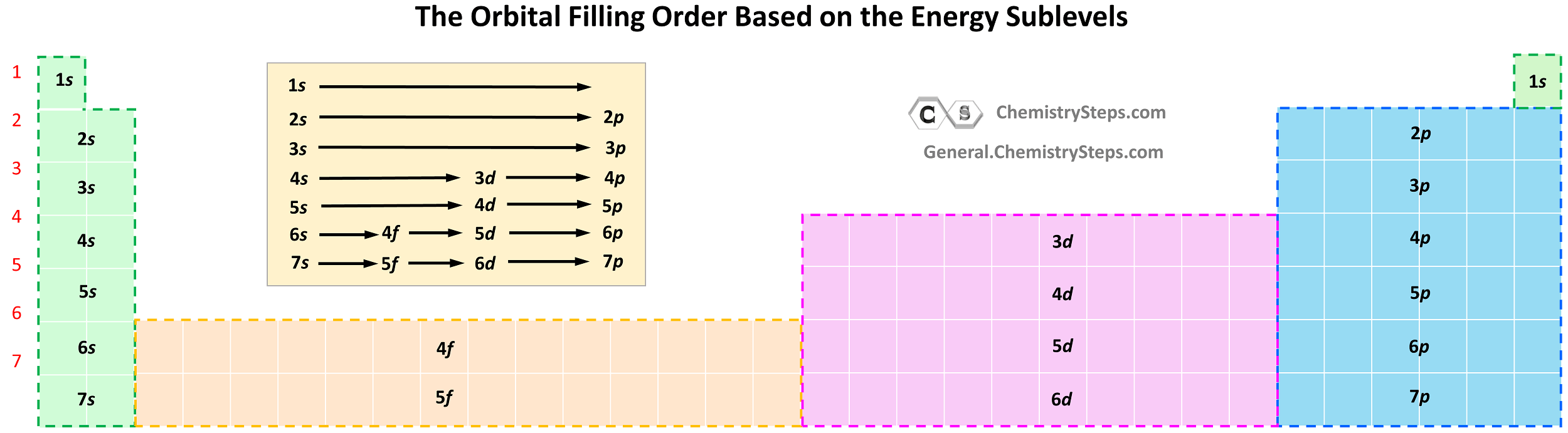
Notice the general filling order is 6s → 4f → 5d, however, ns goes first, then only the first of (n − 1)d, all (n − 2)f, and after that remainder of the (n − 1)d, and np. Therefore, the electron configuration of La is [Xe]6s^²5d^¹ and not [Xe]6s^²4f^¹ as the first d electron goes first.

The inner transition series in Period 7 start after actinium (Ac; Z = 89) and are called the actinides.

Hopefully, you won’t get tested on remembering all these exceptions as it should be the principle that is more important, but in any case, use the ptable.com website to practice filling electron configurations. Just be sure to click the “Electrons” tab in the upper area.

Valence Electrons and Electron Configurations

Valence electrons are the ones farthest away from the nuclei and therefore, we find them in the outermost two orbitals. For example, Li (1s²2s¹) has one valence electron, and it is the 2s orbital. Chlorine (1s^²2s^²2p^⁶3s^²3p^⁵) has seven valence electrons in the 3s and 3p sublevels. If you ever forget, remember that you can easily double-check this based on the group number. The group number indicates the number of valence electrons in the atom.

Electron Configuration of Ions

The first thing you need to remember here is that cations are formed by losing an electron(s), and anions are forming by gaining an electron(s).

The charge of the ion is a result of an imbalance between the number of protons and electrons. If it is a cation, then the positive indicates how many more protons it has compared to the number of electrons. For anions, the charge tells how many extra electrons there are compared to the number of protons.

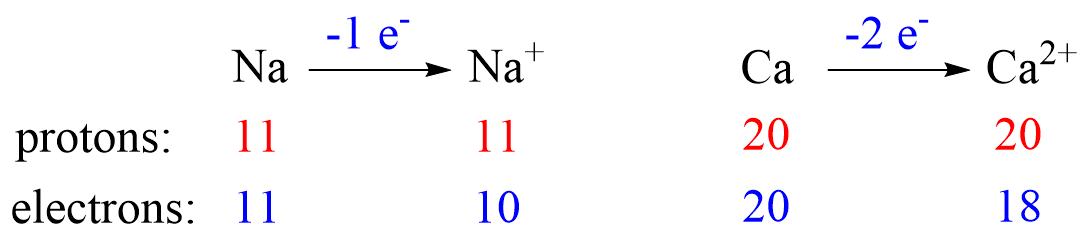
Recall, this pattern for the formation of anions and cations: Metals tend to lose electron(s) and become cations (positively charged ions).

Nonmetals tend to gain an electron(s) and become anions (negatively charged ions).

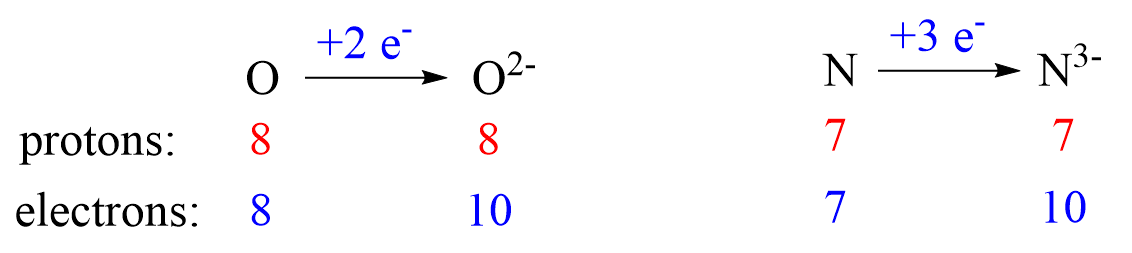
Notice that the number of protons is not changed, and the ions are charged because, unlike atoms, their number of protons and electrons is not equal.

Electron Configuration of Main Group Cations

Now, how do we determine the electron configuration of an ion? If it is, for example, a +1 charged cation, that means the atom has lost one electron. This electron is going to be from the outermost valence shell as these are the electrons farthest away from the nuclei and thus not as strongly attracted to it.

Let’s see an example on Na. It is in the first group, so it loses one electron to become Na⁺.  The electron configuration of sodium is 1s^²2s^²2p^⁶3s^¹, and the electron is removed from the energy level with the greatest n value – 3s. Therefore, the electron configuration of the Na⁺ ion will be 1s^²2s^²2p^⁶:

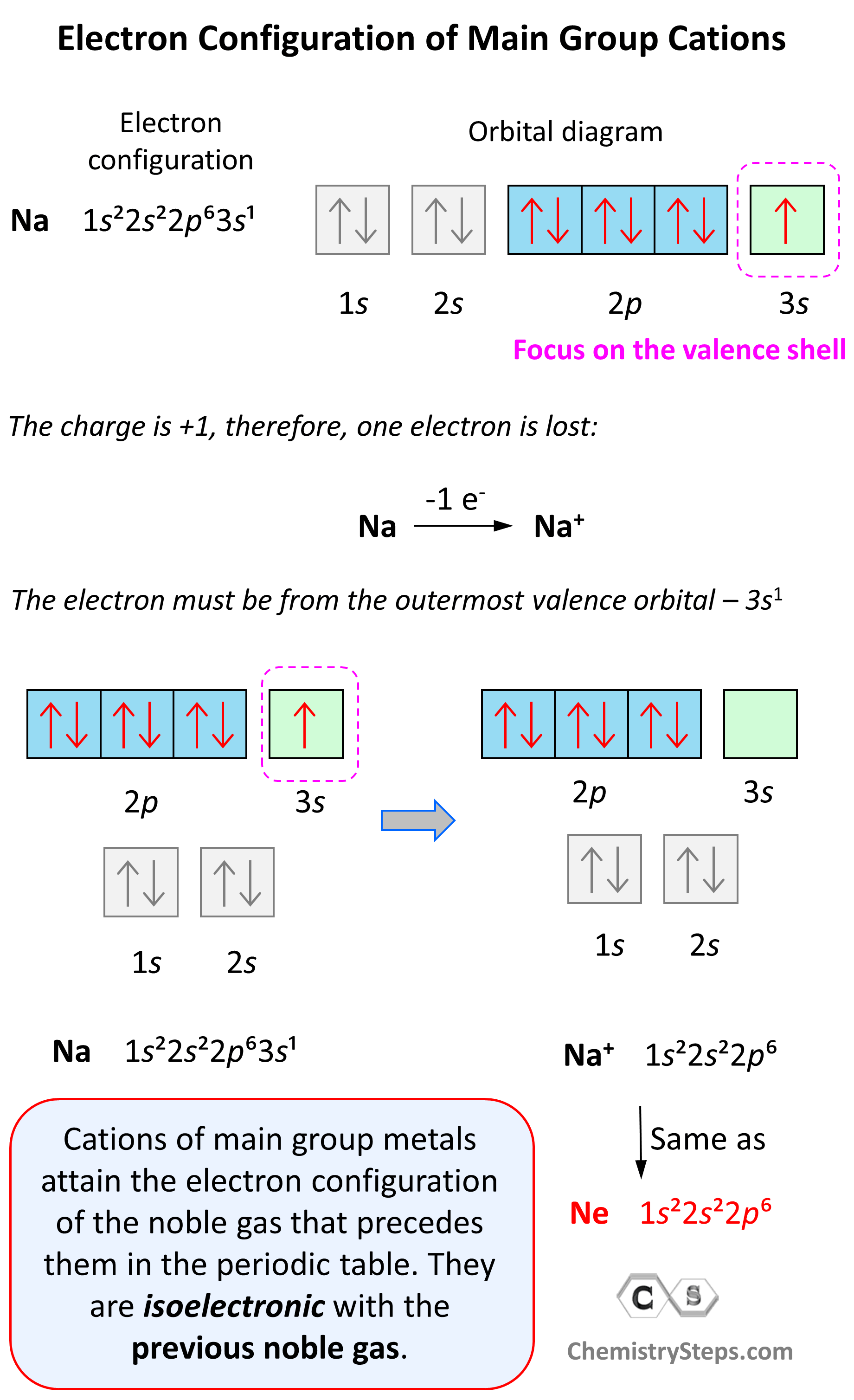
Notice that the ion has a configuration with a complete shell of p orbitals which is characteristic of noble gases. In fact, this is the electron configuration of Ne, and we say that Na⁺ and Ne are isoelectronic (same electronic structure). The reason for this is that, remember, noble gases are very stable because of the low energy level of complete orbitals.

This pattern explains why the metals in the first group become +1, the ones in the second group become +2, and Al, for example, becomes +3. It takes removing one electron from a metal in the first group to obtain the electron configuration of the previous noble gas, it takes two for the group two metals, etc.

Na (1s²2s²2p⁶3s¹) ⟶ e⁻ + Na⁺([He]2s²2p⁶) [isoelectronic with Ne ([He] 2s²2p⁶)]

Electron Configuration of Anions

Anions are formed when the atom gains as many electrons as necessary to attain the electron configuration of the next noble gas in the periodic table. For example, oxygen is in group 6, and therefore, it will need two electrons to attain the electron configuration of Ne:

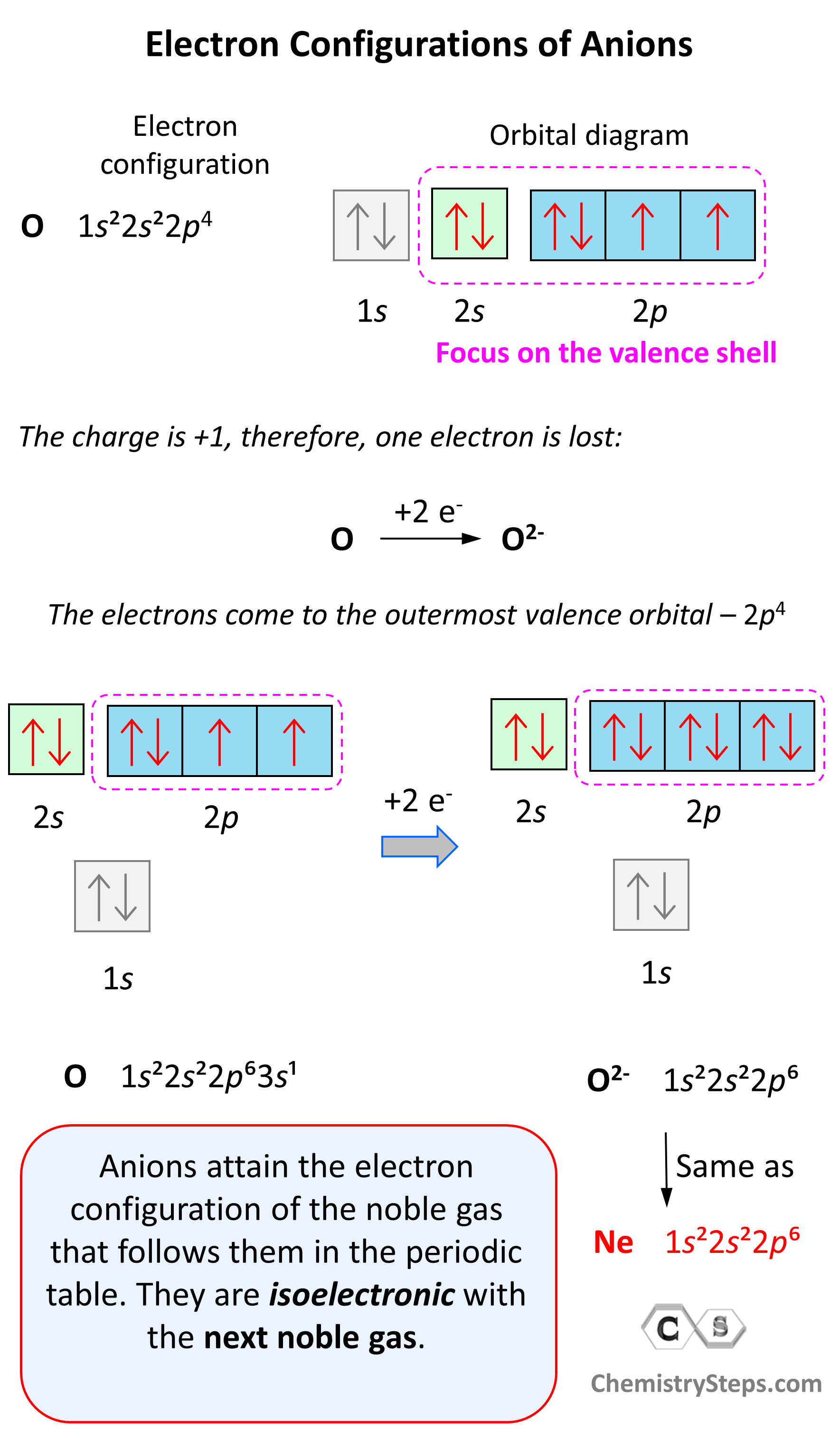
Notice again that the two electrons go to the outermost valence orbital. Oxygen has 6 valence electrons – those in the 2s and 2p orbitals, however, since p sublevels are higher in energy, and they are the only ones capable of accepting additional electrons, the two electrons go to the 2p orbitals. The electron configuration of the oxide ion (O^2-) is therefore, 1s^²2s^²2p^⁶.

O (1s²2s²2p⁴) + 2e⁻⟶ + O^2- ([He]2s²2p⁶) [isoelectronic with Ne ([He] 2s²2p⁶)]

Another common type of monoatomic anions are the halides. Halogens are in group 7, and therefore, they only need one electron to attain the electron configuration of the noble gas following them in the periodic table. For example, bromine takes one electron and becomes isoelectronic to t Kr:

Br([Ar] 4s²3d¹⁰4p⁵) + e⁻ ⟶ Br⁻([Ar] 4s²3d¹⁰4p⁶) [isoelectronic with Kr ([Ar] 4s²3d¹⁰4p⁶)]

Electron Configuration of Transition Metal Cations

In contrast to main-group ions, transition metal ions do not usually attain a noble gas configuration. This is because the ns level is the outermost level, and the (n-1)d is considered an inner level therefore, it will take too much energy to remove those electrons and achieve a noble gas configuration. Therefore, the cation of a transition metal is formed by removing first the electrons from the ns (highest principal quantum number) orbital and then from the (n -1)d orbitals.

For example, the electron configuration of Zn is 1s²2s²2p⁶3s²3p⁶4s²3d¹⁰ or [Ar]4s²3d¹⁰, and it loses the two electrons from the 4s orbital to become Zn²⁺[Ar]3d¹⁰. This is “not a bad” electron configuration considering the filled d orbitals.

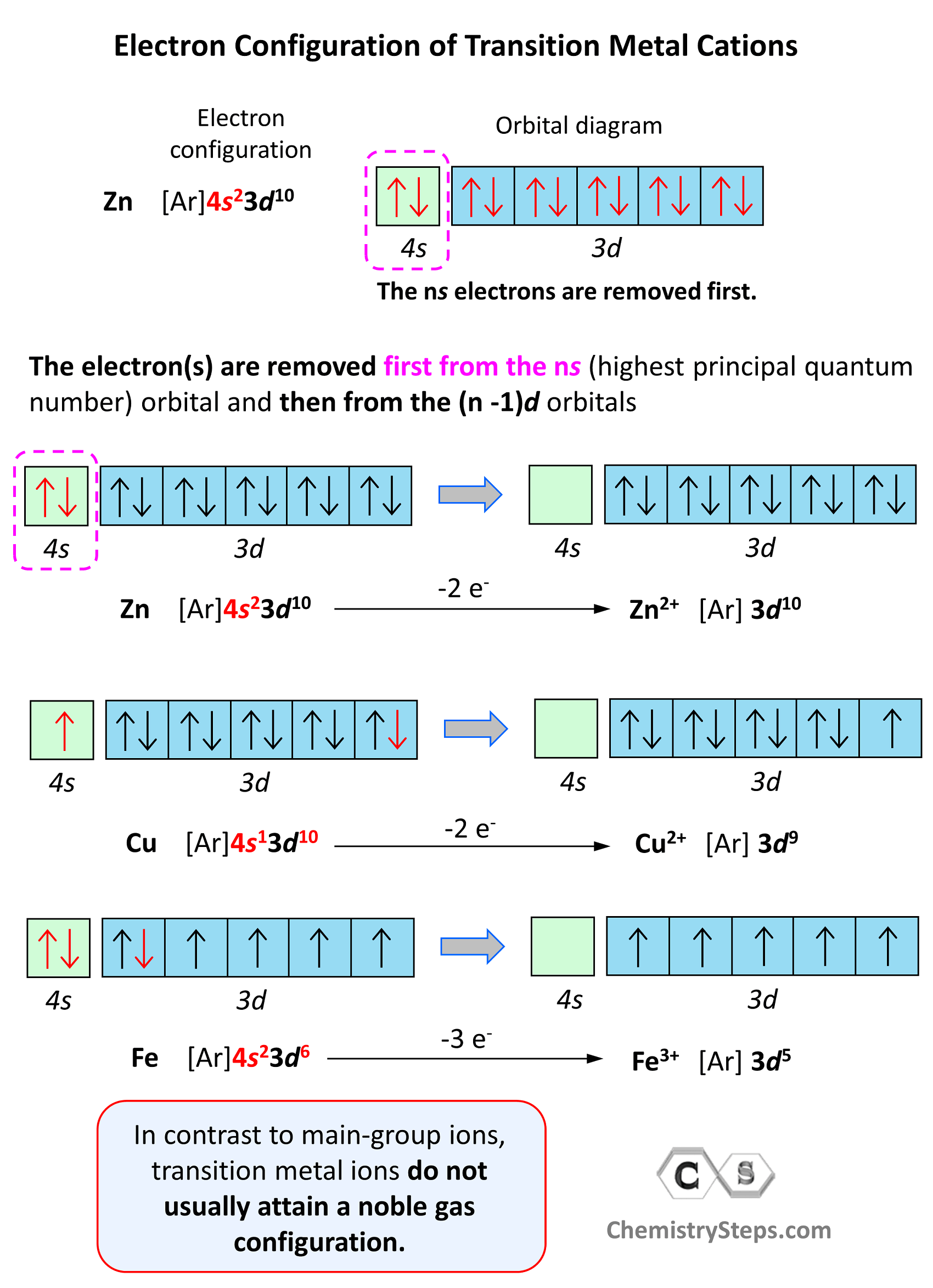
Excited and Ground State Electron Configurations

Remember, when discussing the Bohr model of the hydrogen atom, we mentioned that absorbing light with sufficient energy moves the electron to a higher energy level, and when it falls back to a lower energy level, light is emitted as energy is lost.

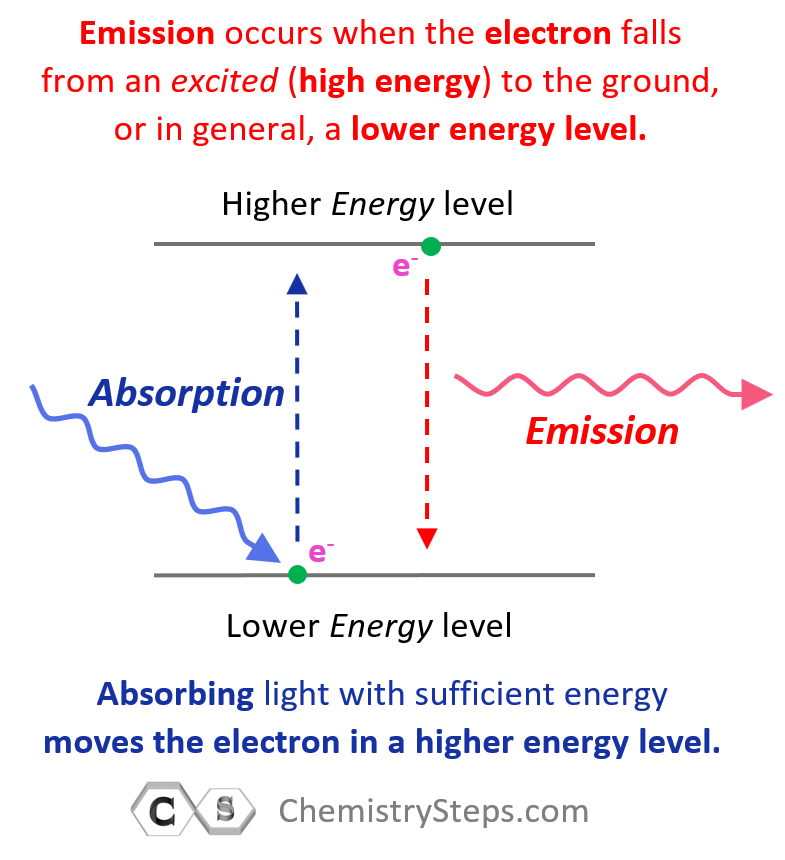
Now, when the electron is in a higher energy level than it normally is, the atom or ion is said to be in the excited state. If the electrons are in the lowest possible energy levels, the atom is in the ground state. So, everything we have discussed today pertains to the electron configurations of atoms at the ground state. In general, unless mentioned otherwise, the term electron configuration refers to the atom in the ground state.

An example of switching from the ground to an excited state can be when the electron in a carbon atom jumps from the 2s to the 2p level. The electron configurations and orbital diagrams can be represented as:

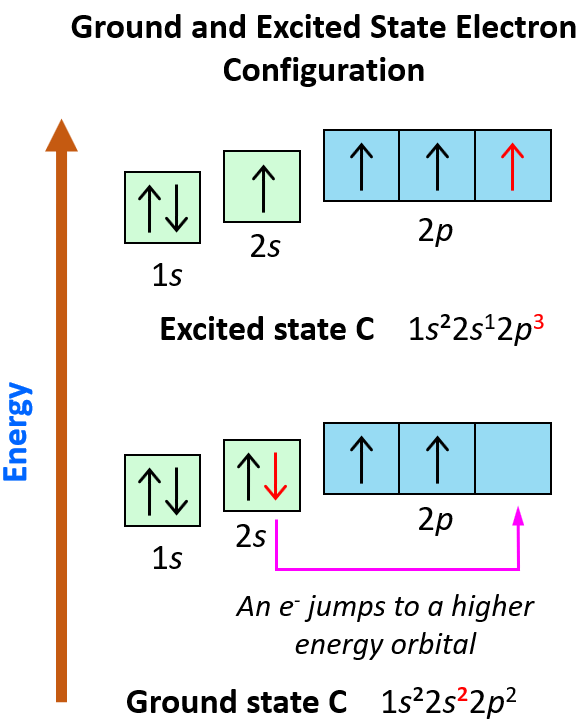
These electron transitions from lower to higher energy orbitals are the basis of many spectroscopies for determining the molecular structures in inorganic and organic materials.

Check Also

• Atomic Orbitals
• Electron Configurations of Ions
• Orbital Diagrams
• Aufbau’s Principle, Hund’s Rule, and Pauli’s Exclusion Principle
• Hund’s Rule
• Pauli Exclusion Principle
• Quantum Numbers (n, l, m_l, m_s)
• Bohr Model of the Hydrogen Atom
• Rydberg Formula
• The Photoelectric Effect
• Calculating The Energy of a Photon
• Ionization Energy
• Electron Affinity
• Energy, Wavelength, and Frequency Practice Problems