This summary practice problem set covers the most common topics of chemical kinetics. You will find questions on the reaction rate, rate constant, rate law, integrated rate law, reaction half-life, and some more.
The links to the corresponding topics are given herein:
- Reaction Rate
- Rate Law and Reaction Order
- How to Determine the Reaction Order
- Integrated Rate Law
- The Half-Life of a Reaction
- Determining the Reaction Order Using Graphs
- Units of Rate Constant k
- How Are Integrated Rate Laws Obtained
- Activation Energy
- The Arrhenius Equation
- Chemical Kinetics Practice Problems
Practice
Review Questions
How is the rate law of a reaction generally determined?
The rate law can only be determined by experiments where the reaction rate is measured by varying the concentration of the reactant(s). The rate law cannot be determined based on the coefficients of a balanced chemical equation.
What do the terms “unimolecular” and “bimolecular” steps mean?
In a unimolecular reaction, only a single reactant participates in the rate-determining step (slowest step) of the reaction. It might be, for example, a decomposition of the reactant to a product(s). In a bimolecular reaction, on the other hand, two molecules collide in the rate-determining step of the reaction to give a product(s).
Why are termolecular steps are not common in chemical reactions?
A reaction between molecules occurs only if they collide with a sufficient energy and proper orientation. The probability of three molecules colliding with these requirements, is very small, making termolecular steps very unlikely.
What are the three variables or factors that can affect the rate of reaction?
As mentioned above, a reaction between molecules occurs only if they collide with a sufficient energy and proper orientation. The frequency of collisions depends on the concentration, so one factor affecting the rate of the reaction is the concentration of the reactants. Although, sometimes, the concentration does not affect the rate of the reaction. The second factor is the temperature since the higher it is, the more energy the reactants have to react. The presence of a catalyst, which is also affects the reaction rate depending on its concertation and surface area, is another factor affecting the reaction rate.
Show how the rate constant units for a zero, first, and second-order reaction can be derived if the concentrations are expressed in mol/L.
Zero-order reaction: k = M/s
First-order reaction: k = s-1
Second-order reaction: k = L mol-1 s-1
Zero-order reaction:
Zero-order indicates that the rate does not depend on the concentration, and therefore, the rate is equal to the concentration.
rate = k
The units for the rate are mol/L, so it is the same as the rate constant:
k = mol/L s or M/s or M x s-1
First-order reaction:
Let’s assume it is a first-order reaction in molecule A:
rate = k[A]
The units for the rate are mol/L. The rate constant is equal to:
\[k\; = \;\frac{{{\rm{rate}}}}{{\left[ {\rm{A}} \right]}}\]
And now, add the units for the rate and concentration:
\[k\; = \;\frac{{{\rm{mol}}}}{{{\rm{L}}\; \times \;{\rm{s}}}}\; \div \;\frac{{{\rm{mol}}}}{{{\rm{L}}\;}}\; = \;\frac{{\cancel{{{\rm{mol}}}}}}{{\cancel{{\rm{L}}}\; \times \;{\rm{s}}}}\; \times \;\frac{{\cancel{{\rm{L}}}}}{{\cancel{{{\rm{mol}}}}}}\; = \;{{\rm{s}}^{{\rm{ – 1}}}}\]
Second-order reaction:
Let’s assume it is a second-order reaction in molecule A:
rate = k[A]2
\[k\; = \;\frac{{{\rm{rate}}}}{{{{\left[ {\rm{A}} \right]}^2}}}\]
And now, add the units for the rate and concentration:
\[k\; = \;\frac{{{\rm{mol}}}}{{{\rm{L}}\; \times \;{\rm{s}}}}\; \div \;{\left( {\frac{{{\rm{mol}}}}{{{\rm{L}}\;}}} \right)^2}\; = \;\frac{{\cancel{{{\rm{mol}}}}}}{{\cancel{{\rm{L}}}\;{\rm{ \times }}\;{\rm{s}}}}\;{\rm{ \times }}\;\frac{{{{\rm{L}}^{\cancel{{\rm{2}}}}}}}{{{\rm{mol}}\cancel{{^{\rm{2}}}}}}\;\;{\rm{ = }}\;\frac{{\rm{L}}}{{{\rm{mol}}\; \times \;{\rm{s}}}}\]
A tiny spark is enough to trigger a highly exothermic explosive reaction between natural gas/gasoline/hydrogen gas, etc.
Explain why a gas container does not explode without this spark.
Even though the explosion is a hugely exothermic reaction with a negative ΔG making it a spontaneous process, it does not occur unless an external energy input is given. This energy is needed to overcome the activation energy of the reaction. Once the spark gives this energy, the combustion reaction of the gas molecules produces more than enough energy to trigger the reaction of the rest.
Sketch a potential-energy diagram for an endothermic, elementary reaction
A + B → C + D
Indicate the reactants, products, the activation energy, the transition state, and the enthalpy change of the reaction.
The reactants are shown on the left, and the products on the right side of energy diagrams. The activation energy (Ea) is the energy gap between the reactants and the transition state, which is the highest energy point of the reaction. The enthalpy change of the reaction is the enthalpy difference between the products and reactions. Because this is an endothermic reaction, products have higher enthalpy than the reactions, and ΔH has a positive sign – energy going to/given to the system.
Molecule A is transformed into molecule D through a multistep reaction. The energy diagram of the reaction is shown below:
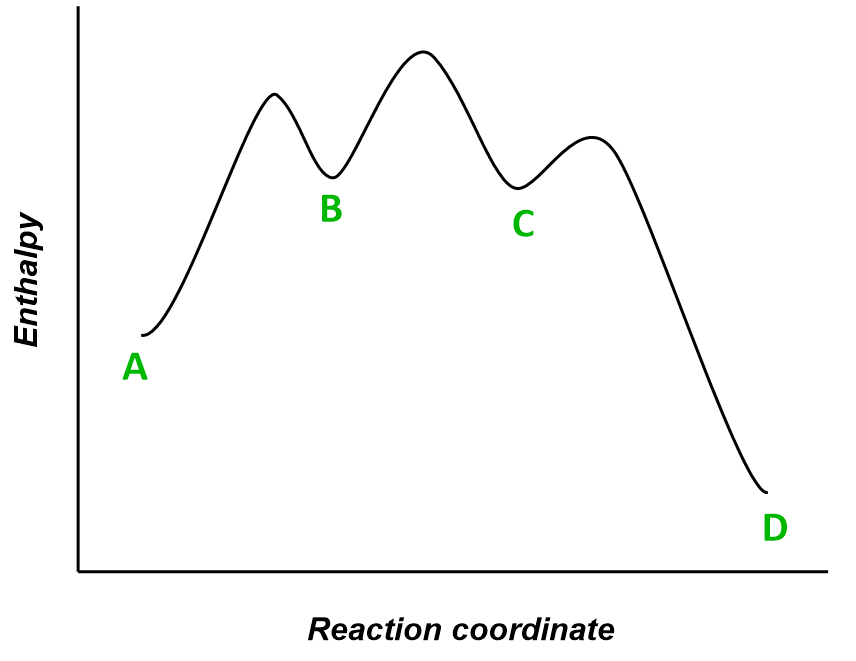
(a) How many intermediates are there in the reaction?
(b) How many transition states are there?
(c) Which is the fastest step in the reaction?
(d) Is the overall reaction exothermic or endothermic?
(a) B and C are the intermediates in this reaction. Remember, intermediates appear after the transition state. They are more stable than transition states, however, not stable enough to be isolated from the reaction mixture.
(b) There are three transition states in this reaction. Transition states are the highest energy peaks in energy diagrams.
(c) The fastest step in the reaction is the one with the lowest activation energy. In this case, it is the conversion n of intermediate C to the final product D.
(d) To determine whether the overall reaction is exothermic or endothermic, compare the energy of the starting material(s) and the product(s). In this reaction, the reactant has higher energy (enthalpy in this case) than the product, and therefore, the overall reaction is exothermic – energy escaping the system?
What is the difference between the rate of a chemical reaction and the rate constant?
The rate constant (k) is a characteristic of a reaction that only depends on temperature. The rate of the reaction, on the other hand, may vary depending on the concentrations. The rate is proportional to the rate constant.
Suppose it is determined that the following reaction is second order:
A + B → C
What are three different expressions for the rate law that can be applicable to the reaction? What does each rate law indicate about the mechanism of the reaction?
The possible rate laws are:
rate = k[A]2, rate = k[A] [B], rate = k [B]2
The possible rate laws are:
rate = k[A]2 ; This means the reaction is second order in A and in the rate-determining step, there are two molecules of A reacting.
rate = k[A] [B]; This means the reaction is first order in A and first order in B, and overall, it is second order. One molecule of A and B react in the rate-determining step of the reaction.
rate = k [B]2 ; This means the reaction is second order in B and in the rate-determining step, there are two molecules of B reacting.
Consider the reactions:
a) 2NO(g) + 2H2(g) → N2(g) + 2H2O(g)
b) 4NH3(g) + 5O2(g) → 4NO(g) + 6H2O(g)
Express the rate of the reaction in terms of the change in concentration of each of the reactants and products.
\[rate\; = \; – \frac{{\rm{1}}}{{\rm{2}}}\frac{{{\rm{\Delta }}\left[ {{\rm{NO}}} \right]}}{{{\rm{\Delta t}}}}\; = \; – \frac{{\rm{1}}}{{\rm{2}}}\frac{{{\rm{\Delta }}\left[ {{{\rm{H}}_{\rm{2}}}} \right]}}{{{\rm{\Delta t}}}}\; = \;\frac{{{\rm{\Delta }}\left[ {{{\rm{N}}_{\rm{2}}}} \right]}}{{{\rm{\Delta t}}}}\; = \;\frac{{\rm{1}}}{{\rm{2}}}\frac{{{\rm{\Delta }}\left[ {{{\rm{H}}_{\rm{2}}}{\rm{O}}} \right]}}{{{\rm{\Delta t}}}}\]
\[rate\; = \; – \frac{{\rm{1}}}{{\rm{4}}}\frac{{{\rm{\Delta }}\left[ {{\rm{N}}{{\rm{H}}_{\rm{3}}}} \right]}}{{{\rm{\Delta t}}}}\; = \; – \frac{{\rm{1}}}{{\rm{5}}}\frac{{{\rm{\Delta }}\left[ {{{\rm{O}}_{\rm{2}}}} \right]}}{{{\rm{\Delta t}}}}\; = \;\frac{{\rm{1}}}{{\rm{4}}}\frac{{{\rm{\Delta }}\left[ {{\rm{NO}}} \right]}}{{{\rm{\Delta t}}}}\; = \;\frac{{\rm{1}}}{{\rm{6}}}\frac{{{\rm{\Delta }}\left[ {{{\rm{H}}_{\rm{2}}}{\rm{O}}} \right]}}{{{\rm{\Delta t}}}}\]
The general formula for the reaction rate based on the coefficients can be written as:
aA + bB → cC + dD
\[{\rm{Rate}}\; = \; – \frac{{\rm{1}}}{{\rm{a}}}\frac{{{\rm{\Delta }}\left[ {\rm{A}} \right]}}{{{\rm{\Delta t}}}}\; = \; – \frac{{\rm{1}}}{{\rm{b}}}\frac{{{\rm{\Delta }}\left[ {\rm{B}} \right]}}{{{\rm{\Delta t}}}}\; = \; + \frac{{\rm{1}}}{{\rm{c}}}\frac{{{\rm{\Delta }}\left[ {\rm{C}} \right]}}{{{\rm{\Delta t}}}}\; = \; + \frac{{\rm{1}}}{{\rm{d}}}\frac{{{\rm{\Delta }}\left[ {\rm{D}} \right]}}{{{\rm{\Delta t}}}}\]
where A and B are reactants, C and D are products, and a, b, c, and d are the stoichiometric coefficients.
a) \[rate\; = \; – \frac{{\rm{1}}}{{\rm{2}}}\frac{{{\rm{\Delta }}\left[ {{\rm{NO}}} \right]}}{{{\rm{\Delta t}}}}\; = \; – \frac{{\rm{1}}}{{\rm{2}}}\frac{{{\rm{\Delta }}\left[ {{{\rm{H}}_{\rm{2}}}} \right]}}{{{\rm{\Delta t}}}}\; = \;\frac{{{\rm{\Delta }}\left[ {{{\rm{N}}_{\rm{2}}}} \right]}}{{{\rm{\Delta t}}}}\; = \;\frac{{\rm{1}}}{{\rm{2}}}\frac{{{\rm{\Delta }}\left[ {{{\rm{H}}_{\rm{2}}}{\rm{O}}} \right]}}{{{\rm{\Delta t}}}}\]
b) \[rate\; = \; – \frac{{\rm{1}}}{{\rm{4}}}\frac{{{\rm{\Delta }}\left[ {{\rm{N}}{{\rm{H}}_{\rm{3}}}} \right]}}{{{\rm{\Delta t}}}}\; = \; – \frac{{\rm{1}}}{{\rm{5}}}\frac{{{\rm{\Delta }}\left[ {{{\rm{O}}_{\rm{2}}}} \right]}}{{{\rm{\Delta t}}}}\; = \;\frac{{\rm{1}}}{{\rm{4}}}\frac{{{\rm{\Delta }}\left[ {{\rm{NO}}} \right]}}{{{\rm{\Delta t}}}}\; = \;\frac{{\rm{1}}}{{\rm{6}}}\frac{{{\rm{\Delta }}\left[ {{{\rm{H}}_{\rm{2}}}{\rm{O}}} \right]}}{{{\rm{\Delta t}}}}\]
Consider the reaction of HCl forming H2 and Cl2 gases:
2HCl(g) → H2(g) + Cl2(g)
a) What is the average rate of the reaction during the first 30.0 s if the concentration of HCl dropped from 0.750 M to 0.430 M?
b) If the volume of the reaction is 2.50 L, what amount of Cl2 (in moles) will be formed during the first 20.0 s of the reaction?
a) 3.56 × 10–3 M/s
b) 0.178 mol
a) We need to write the equation for rate based on the concentration of HCl. Because the HCl is a reactant, its concentration is decreasing and a negative sign is added.
\[rate\; = \; – \frac{{\rm{1}}}{{\rm{2}}}\frac{{{\rm{\Delta }}\left[ {{\rm{HCl}}} \right]}}{{{\rm{\Delta t}}}}\; = \; – \frac{{\rm{1}}}{{\rm{2}}}\frac{{{{\left[ {{\rm{HCl}}} \right]}_t}_{_2}\; – \;{{\left[ {{\rm{HCl}}} \right]}_t}_{_1}}}{{{\rm{\Delta t}}}}\]
\[rate\; = \; – \frac{{\rm{1}}}{{\rm{2}}}\frac{{{\rm{\Delta }}\left[ {{\rm{HCl}}} \right]}}{{{\rm{\Delta t}}}}\; = \; – \frac{{\rm{1}}}{{\rm{2}}}\frac{{{\rm{0}}{\rm{.430}}\;{\rm{M}}\;{\rm{ – }}\;{\rm{0}}{\rm{.750}}\;{\rm{M}}}}{{{\rm{45.0}}\;{\rm{s}}\;{\rm{ – }}\;{\rm{0}}\;{\rm{s}}}}\;{\rm{ = }}\;{\rm{3}}{\rm{.56}}\;{\rm{ \times }}\;{\rm{1}}{{\rm{0}}^{{\rm{ – 3}}}}\;{\rm{M/s}}\]
b) To find the number of Cl2 moles produced in the first 20.0 s, let’s first determine its concentration after 20.0 s. For this, we need to rearrange the equation for rate:
\[rate\; = \;\frac{{{\rm{\Delta }}\left[ {{\rm{C}}{{\rm{l}}_{\rm{2}}}} \right]}}{{{\rm{\Delta t}}}}\;\]
\[{\rm{\Delta }}\left[ {{\rm{C}}{{\rm{l}}_{\rm{2}}}} \right]\; = \;rate\; \times \;{\rm{\Delta t}}\;\]
\[{\rm{\Delta }}\left[ {{\rm{C}}{{\rm{l}}_{\rm{2}}}} \right]\;{\rm{ = }}\;{\rm{3}}{\rm{.56 \times 1}}{{\rm{0}}^{{\rm{–3}}}}{\rm{M/s}}\;{\rm{ \times }}\;{\rm{20}}{\rm{.0}}\;{\rm{s}}\;{\rm{ = }}\;{\rm{0}}{\rm{.0712}}\;{\rm{M}}\;\]
Th last part is to convert the concentration to moles:
n (Cl2) = M·V = 0.0712 mol/L x 2.50 L = 0.178 mol
Consider the Haber process for the synthesis of ammonia:
3H2(g) + N2(g) ⇆ 2NH3(g)
In the first 25.0 s of this reaction, the concentration of H2 dropped from 0.600 M to 0.512 M. Calculate the average rate of the reaction during this time interval.
1.17 x 10-3 M/s
\[rate\; = \; – \frac{{\rm{1}}}{{\rm{3}}}\frac{{{\rm{\Delta }}\left[ {{{\rm{H}}_{\rm{2}}}} \right]}}{{{\rm{\Delta t}}}}\;\]
\[rate\; = \; – \frac{{\rm{1}}}{{\rm{3}}}\frac{{{\rm{0}}{\rm{.512}}\;{\rm{M}}\;{\rm{ – }}\;{\rm{0}}{\rm{.600}}\;{\rm{M}}}}{{{\rm{25}}{\rm{.0}}\;{\rm{s}}\; – \;0\;s}}\; = \;1.17\; \times \;{10^{ – 3}}\;{\rm{M/s}}\;\]
At what rate is ammonia being formed in the previous example?
3H2(g) + N2(g) ⇆ 2NH3(g)
rate = 1.17 x 10-3 M/s
2.34 x 10-3 M/s
\[rate\; = \;\frac{{\rm{1}}}{{\rm{2}}}\frac{{{\rm{\Delta }}\left[ {{\rm{N}}{{\rm{H}}_{\rm{3}}}} \right]}}{{{\rm{\Delta t}}}}\]
\[\frac{{{\rm{\Delta }}\left[ {{\rm{N}}{{\rm{H}}_{\rm{3}}}} \right]}}{{{\rm{\Delta t}}}}\; = \;rate\; \times \;2\; = \;2\; \times \;1.17{\rm{ }} \times {\rm{ }}{10^{ – 3}}M/s\; = \;2.34\; \times {\rm{ }}{10^{ – 3}}\;M/s\]
Consider the following decomposition reaction of SO3:
2SO3(g) → 2SO2(g) + O2(g)
During the first 75.0 s, the concentration of SO3 decreased from 0.265 mol/L to 0.189 mol/L. Determine the average rate of decomposition of SO3 during this time interval in mol/(L s).
5.07 × 10-4 M/s
\[rate\; = \; – \frac{{\rm{1}}}{{\rm{2}}}\frac{{{\rm{\Delta }}\left[ {{\rm{S}}{{\rm{O}}_{\rm{3}}}} \right]}}{{{\rm{\Delta t}}}}\; = \; – \frac{{\rm{1}}}{{\rm{2}}}\frac{{0.189\;{\rm{M}}\;{\rm{ – }}\;{\rm{0}}{\rm{.265}}\;{\rm{M}}}}{{{\rm{75.0}}\;{\rm{s}}\;{\rm{ – }}\;{\rm{0}}\;{\rm{s}}}}\;{\rm{ = }}\;{\rm{5}}{\rm{.07}}\;{\rm{ \times }}\;{\rm{1}}{{\rm{0}}^{{\rm{ – 4}}}}\;{\rm{M/s}}\]
Consider the reaction:
4NH3(g) + 5O2(g) → 4NO(g) + 6H2O(g)
Using the rate for the disappearance of NH3, fill out the missing data in the table.
| Δ[NH3]/Δt | Δ[O2]/Δt | Δ[NO]/Δt | Δ[H2O]/Δt | rate |
| -0.954 M/s |
Let’s first write the expression for the rate of the reaction using all the reactants and products:
\[rate\; = \; – \frac{{\rm{1}}}{{\rm{4}}}\frac{{{\rm{\Delta }}\left[ {{\rm{N}}{{\rm{H}}_{\rm{3}}}} \right]}}{{{\rm{\Delta t}}}}\; = \; – \frac{{\rm{1}}}{{\rm{5}}}\frac{{{\rm{\Delta }}\left[ {{{\rm{O}}_{\rm{2}}}} \right]}}{{{\rm{\Delta t}}}}\; = \;\frac{{\rm{1}}}{{\rm{4}}}\frac{{{\rm{\Delta }}\left[ {{\rm{NO}}} \right]}}{{{\rm{\Delta t}}}}\; = \;\frac{{\rm{1}}}{{\rm{6}}}\frac{{{\rm{\Delta }}\left[ {{{\rm{H}}_{\rm{2}}}{\rm{O}}} \right]}}{{{\rm{\Delta t}}}}\]
To find the rate of O2 depletion, we keep the two corresponding parts of the equation:
\[ – \frac{{\rm{1}}}{{\rm{4}}}\frac{{{\rm{\Delta }}\left[ {{\rm{N}}{{\rm{H}}_{\rm{3}}}} \right]}}{{{\rm{\Delta t}}}}\; = \; – \frac{{\rm{1}}}{{\rm{5}}}\frac{{{\rm{\Delta }}\left[ {{{\rm{O}}_{\rm{2}}}} \right]}}{{{\rm{\Delta t}}}}\;\]
\[\frac{{{\rm{\Delta }}\left[ {{{\rm{O}}_{\rm{2}}}} \right]}}{{{\rm{\Delta t}}}}\; = \;\frac{{\rm{5}}}{{\rm{4}}}\frac{{{\rm{\Delta }}\left[ {{\rm{N}}{{\rm{H}}_{\rm{3}}}} \right]}}{{{\rm{\Delta t}}}}\;\]
\[\frac{{{\rm{\Delta }}\left[ {{{\rm{O}}_{\rm{2}}}} \right]}}{{{\rm{\Delta t}}}}\;{\rm{ = }}\;\frac{{\rm{5}}}{{\rm{4}}}\;{\rm{ \times }}\;{\rm{( – 0}}{\rm{.954}}\;{\rm{M/s)}}\; = \; – 1.19\;{\rm{M/s}}\]
To find the rate of NO formation, we keep the two corresponding parts of the equation:
\[ – \frac{{\rm{1}}}{{\rm{4}}}\frac{{{\rm{\Delta }}\left[ {{\rm{N}}{{\rm{H}}_{\rm{3}}}} \right]}}{{{\rm{\Delta t}}}}\; = \;\frac{{\rm{1}}}{{\rm{4}}}\frac{{{\rm{\Delta }}\left[ {{\rm{NO}}} \right]}}{{{\rm{\Delta t}}}}\;\]
\[\frac{{{\rm{\Delta }}\left[ {{\rm{NO}}} \right]}}{{{\rm{\Delta t}}}}\; = \; – \frac{{{\rm{\Delta }}\left[ {{\rm{N}}{{\rm{H}}_{\rm{3}}}} \right]}}{{{\rm{\Delta t}}}}\]
\[\frac{{{\rm{\Delta }}\left[ {{\rm{NO}}} \right]}}{{{\rm{\Delta t}}}}\; = \;0.954\;M/s\]
To find the rate of H2O formation, we keep the two corresponding parts of the equation:
\[ – \frac{{\rm{1}}}{{\rm{4}}}\frac{{{\rm{\Delta }}\left[ {{\rm{N}}{{\rm{H}}_{\rm{3}}}} \right]}}{{{\rm{\Delta t}}}}\; = \;\frac{{\rm{1}}}{{\rm{6}}}\frac{{{\rm{\Delta }}\left[ {{{\rm{H}}_{\rm{2}}}{\rm{O}}} \right]}}{{{\rm{\Delta t}}}}\]
\[\frac{{{\rm{\Delta }}\left[ {{{\rm{H}}_{\rm{2}}}{\rm{O}}} \right]}}{{{\rm{\Delta t}}}} = – \frac{{\rm{6}}}{{\rm{4}}}\frac{{{\rm{\Delta }}\left[ {{\rm{N}}{{\rm{H}}_{\rm{3}}}} \right]}}{{{\rm{\Delta t}}}}\]
\[\frac{{{\rm{\Delta }}\left[ {{{\rm{H}}_{\rm{2}}}{\rm{O}}} \right]}}{{{\rm{\Delta t}}}} = – \frac{{\rm{6}}}{{\rm{4}}}\; \times \;{\rm{0}}{\rm{.954}}\;{\rm{M/s}}\;{\rm{ = }}\;{\rm{1}}{\rm{.43}}\;{\rm{M/s}}\]
The rate of the reaction is:
\[rate\; = \; – \frac{{\rm{1}}}{{\rm{4}}}\frac{{{\rm{\Delta }}\left[ {{\rm{N}}{{\rm{H}}_{\rm{3}}}} \right]}}{{{\rm{\Delta t}}}}\; = \; – \frac{{\rm{1}}}{{\rm{4}}}\; \times \;0.954\;M/s\; = \;0.239\;M/s\]
Adding the data to the table, we get:
4NH3(g) + 5O2(g) → 4NO(g) + 6H2O(g)
| Δ[NH3]/Δt | Δ[O2]/Δt | Δ[NO]/Δt | Δ[H2O]/Δt | rate |
| -0.954 M/s | –1.19 M/s | 0.954 M/s | 1.43 M/s | 0.239 M/s |
I put the chemical equation on top so that you can compare the values and see if they make sense based on the coefficients.
O2 decreases a little faster than NH3 because of the 5:4 ratio so this is reasonable. NO is forming at the same rate as NH3 disappears, and having a 1:1 ratio makes this correct too. The increase in H2O concentration should be 1.5 times higher than the decrease of the NH3 concentration based on the 6:4 ratio, and that is what we got. The rate of the reaction can be determined by dividing the disappearance or formation rate of any component by its coefficient and as expected, it is the smallest among all.
Iron(II) ion is oxidized by hydrogen peroxide in an acidic solution.
2Fe2+ (aq) + H2O2(aq) + 2H+(aq) → 2Fe3+(aq) + 2H2O(l)
The rate law for the reaction is determined to be rate = k[H2O2 ][Fe2+]. The rate constant, at certain temperature, is 2.56 x 1024/M · s. Calculate the rate of the reaction at this temperature if [H2O2 ] = 0.48 M and [H2O2] = 0.070 M.
8.60 x 102 M/s
rate = k[H2O2 ][Fe2+]
rate = 2.56 x 104/M · s (0.48 M) (0.070 M) = 8.60 x 102 M/s
For the kinetics of the reaction
2NO(g) + Cl2(g) → 2NOCl(g)
The following data were obtained:
| Exp. | [NO] | [Cl2] | Initial rate, M/s |
| 1 | 0.25 | 0.35 | 0.68 |
| 2 | 0.25 | 0.70 | 1.36 |
| 3 | 0.50 | 0.70 | 2.72 |
a) What is reaction order in Cl2 and NO?
b) What is the rate law?
c) What is the value of the rate constant?
a) First-order in both NO and Cl2
b) Second-order
c) 7.77 s-1 M-1
Let’s put the table here and work on the questions:
| Exp. | [NO] | [Cl2] | Initial rate, M/s |
| 1 | 0.25 | 0.35 | 0.68 |
| 2 | 0.25 | 0.70 | 1.36 |
| 3 | 0.50 | 0.70 | 2.72 |
a) To determine the rate law, we need to know the order of the reaction in both reactants. To determine the reaction order in NO, find two experiments where the concentration of Cl2 is kept constant while the concentration of NO is changed. In experiments 2 and 3, the concentration of Cl2 is kept at 0.70 M, while that of NO is doubled from 0.25 M to 0.50 M.
Now, let’s see how the rate has changed in these two experiments:
\[\frac{{{\rm{rat}}{{\rm{e}}_{\rm{3}}}}}{{{\rm{rat}}{{\rm{e}}_{\rm{2}}}}} = \frac{{2.72}}{{1.36}}\; = \;2\]
The rate of the reaction has also doubled as a result of this change, and therefore, the reaction with respect to NO is first order.
To determine the reaction order in Cl2, find two experiments where the concentration of NO is kept constant while the concentration of Cl2 is changed. In experiments 1 and 2, the concentration of NO is kept at 0.25 M, while that of Cl2 is doubled from 0.35 to 0.70.
Now, let’s see how the rate has changed in these two experiments:
\[\frac{{{\rm{rat}}{{\rm{e}}_{\rm{2}}}}}{{{\rm{rat}}{{\rm{e}}_{\rm{1}}}}} = \frac{{1.36}}{{0.68}}\; = \;2\]
The rate of the reaction has also doubled as a result of this change, and therefore, the reaction with respect to Cl2 is first order.
b) Because the reaction is first-order in each reactant, the rate law of the reaction is rate = k[NO][Cl2]
c) To determine the value of the rate constant, we need to write the expression for the reaction rate:
rate = k[NO][Cl2]
Now, you can pick data from any experiment and plug the numbers into a rate law experiment. Let’s use the data from experiment 1.
rate = k[NO][Cl2]
\[k = \frac{{{\rm{rat}}{{\rm{e}}_{\rm{1}}}}}{{\left[ {{\rm{NO}}} \right]\left[ {{\rm{C}}{{\rm{l}}_{\rm{2}}}} \right]}}\;\]
\[k = \frac{{{\rm{0}}{\rm{.68}}\;\cancel{{\rm{M}}}{\rm{/s}}}}{{{\rm{0}}{\rm{.25}}\;\cancel{{\rm{M}}}\;{\rm{ \times }}\;{\rm{0}}{\rm{.35}}\;{\rm{M}}}}\; = \;7.77\;{s^{ – 1}}\;{M^{ – 1}}\;\]
The date for the initial rate of the following reaction is listed in the table below:
A + B → C + D
| Exp. | [A] | [B] | Initial rate, M/s |
| 1 | 0.370 | 0.248 | 2.45 x 10-3 |
| 2 | 0.370 | 0.496 | 9.8 x 10-3 |
| 3 | 0.740 | 0.248 | 4.9 x 10-3 |
| 4 | 0.740 | 0.496 | 1.96 x 10-2 |
(a) What is the order of reaction with respect to A and to B?
(b) What is the overall reaction order?
(c) What is the value of the rate constant, k?
) First order in A, and second-order in B
b) Third-order overall
c) 0.108 M–2s–1
Let’s put the table here and work on the questions:
| Exp. | [A] | [B] | Initial rate, M/s |
| 1 | 0.370 | 0.248 | 2.45 x 10-3 |
| 2 | 0.370 | 0.496 | 9.8 x 10-3 |
| 3 | 0.740 | 0.248 | 4.9 x 10-3 |
| 4 | 0.740 | 0.496 | 1.96 x 10-2 |
a) To determine the reaction order in B, find two experiments where the concentration of A is kept constant while the concentration of B is changed. In experiments 1 and 2, the concentration of A is kept at 0.370 M, while that of B is doubled from 0.248 M to 0.496 M.
Now, let’s see how the rate has changed in these two experiments:
\[\frac{{{\rm{rat}}{{\rm{e}}_{\rm{3}}}}}{{{\rm{rat}}{{\rm{e}}_{\rm{1}}}}} = \frac{{4.9{\rm{ }} \times {\rm{ }}{{10}^{ – 3}}}}{{2.45{\rm{ }} \times {\rm{ }}{{10}^{ – 3}}}}\; = \;2\]
The rate of the reaction has also doubled as a result of this change, and therefore, the reaction with respect to A is first order.
To determine the reaction order in A, find two experiments where the concentration of B is kept constant while the concentration of A is changed. In experiments 1 and 3, the concentration of B is kept at 0.248 M, while that of A is doubled from 0.370 to 0.740.
Now, let’s see how the rate has changed in these two experiments:
\[\frac{{{\rm{rat}}{{\rm{e}}_{\rm{2}}}}}{{{\rm{rat}}{{\rm{e}}_{\rm{1}}}}} = \frac{{9.8{\rm{ }} \times {\rm{ }}{{10}^{ – 3}}}}{{2.45{\rm{ }} \times {\rm{ }}{{10}^{ – 3}}}}\; = \;4\]
The rate of the reaction has quadrupled as a result of this change, and therefore, the reaction with respect to B is second order.
b) Because the reaction is first order in one reactant, and second-order in the other reactant, overall it is a third-order reaction.
c) To determine the value of the rate constant, you can pick data from any experiment and plug the numbers into a rate law experiment. Let’s use the data from experiment 1. Remember, the reaction is first order in A, and second order in B:
rate1 = k[A][B]2
\[k = \frac{{{\rm{rat}}{{\rm{e}}_{\rm{1}}}}}{{\left[ {\rm{A}} \right]{{\left[ {\rm{B}} \right]}^{\rm{2}}}}}\;\]
\[k = \frac{{{\rm{2}}{\rm{.45 \times 1}}{{\rm{0}}^{{\rm{ – 3}}}}\;\cancel{{\rm{M}}}{\rm{/s}}}}{{{\rm{0}}{\rm{.370}}\;\cancel{{\rm{M}}}\;{{\left( {{\rm{0}}{\rm{.248}}\;{\rm{M}}} \right)}^{\rm{2}}}}}\; = \;0.108\;{{\rm{M}}^{{\rm{ – 2}}}}{{\rm{s}}^{{\rm{ – 1}}}}\;\]
Consider the reaction
A(g) + B(g) ⇌ C(g)
The following data were obtained at a certain temperature:
| Exp. | [A] | [B] | Initial rate, M/s |
| 1 | 2.40 | 3.60 | 4.8 x 10-2 |
| 2 | 2.40 | 7.20 | 4.8 x 10-2 |
| 3 | 4.80 | 3.60 | 9.6 x 10-2 |
Using the data, determine the order of the reaction and calculate the rate constant:
rate = k [A]
k = 0.020 s–1
a) To determine the overall reaction order, we need to determine it with respect to both reactants. Let’s first determine the order in A. Find two experiments where the concentration of B is kept constant while the concentration of A is changed. In experiments 1 and 3, the concentration of A is doubled from 2.40 M to 4.80 M while the concentration of B is kept at 3.60 M. We see from the table, that doubling the concentration of A had also doubled the rate of the reaction. Therefore, the reaction is first order in A.
Now, let’s find two experiments where the concentration of A is kept constant while that of B is changed. In experiments 1 and 2, the concentration of A is kept at 2.40 M while the concentration of B is doubled from 3.60 M to 7.20 M. We see from the table, that doubling the concentration of B had no effect on the rate of the reaction as it remained at 4.8 x 10-2 M/s. Therefore, the reaction is zero order in B.
The overall order of the reaction is, therefore, first order:
rate = k [A]
b) To determine the value of the rate constant, we can pick data from any experiment and plug the numbers into a rate law experiment. Let’s use the data from experiment 1.
rate = k [A]
k = rate/ [A]
\[k = \frac{{4.8{\rm{ }} \times {\rm{ }}{{10}^{ – 2}}\;\cancel{{\rm{M}}}{\rm{/s}}}}{{{\rm{2}}{\rm{.40}}\;\cancel{{\rm{M}}}\;}}\; = \;0.020\;{s^{ – 1}}\]
\[k = \frac{{4.8{\rm{ }} \times {\rm{ }}{{10}^{ – 2}}\;\cancel{{\rm{M}}}{\rm{/s}}}}{{{\rm{2}}{\rm{.40}}\;\cancel{{\rm{M}}}\;}}\; = \;0.020\;{s^{ – 1}}\]
Carbon dioxide, CO2, reacts with hydrogen to give methanol (CH3OH), and water.
CO2(g) + 3H2(g) ⇆ CH3OH(g) + H2O(g)
In a series of experiments, the following initial rates of disappearance of CO2 were obtained:
| Exp. | [CO2] | [H2] | Initial rate, M/s |
| 1 | 0.640 | 0.220 | 2.7 x 10-3 |
| 2 | 1.28 | 0.220 | 1.08 x 10-2 |
| 3 | 0.640 | 0.440 | 5.4 x 10-3 |
Determine the rate law and calculate the value of the rate constant for this reaction.
The rate law is Rate = k[CO2]2[H2]
3.00 × 10-2 M-2 s-1
Like we did for the previous examples, find two experiments where the concentration of one reactant is varied while the other’s is kept constant.
From experiments 1 and 2, we see that doubling [CO2] quadruples the rate, so the reaction is second order in CO2.
Experiments 1 and 3: Doubling [H2] doubles the rate, so the reaction is first order in H2. The rate law should have the form:
Rate = k[CO2]2[H2]
To calculate the value of the rate constant, use the numbers from any experiment for the following equation:
\[k\; = \;\frac{{{\rm{rate}}}}{{{{\left[ {{\rm{C}}{{\rm{O}}_{\rm{2}}}} \right]}^2}\left[ {{{\rm{H}}_{\rm{2}}}} \right]}}\]
\[k\; = \;\frac{{{\rm{2}}{\rm{.7 \times 1}}{{\rm{0}}^{{\rm{ – 3}}}}\;\cancel{{\rm{M}}}{\rm{/s}}}}{{{{\left( {{\rm{0}}{\rm{.640}}\;{\rm{M}}} \right)}^{\rm{2}}}\left( {{\rm{0}}{\rm{.220}}\;\cancel{{\rm{M}}}} \right)}}\;{\rm{ = }}\;{\rm{3}}{\rm{.00 \times 1}}{{\rm{0}}^{{\rm{ – 2}}}}\;{{\rm{M}}^{{\rm{ – 2}}}}{{\rm{s}}^{{\rm{ – 1}}}}\;\]
Integrated Rate Laws
Dinitrogen pentoxide, N2O5, decomposes when heated.
2N2O5(g) → 2N2O4(g) + O2(g) k = 3.4 x 10-6/s
What would be the concentration of N2O5 after running the reaction for 3.0 hr if the initial concentration of N2O5 was 0.0465 mol/L?
Hint, first determine the reaction order based on the units of k.
[N2O5]t = 0.0448 M
You should recognize from the units of the rate constant that it is a first-order reaction. The integrated rate law for first-order reactions can be written as:
ln [A]t = -kt + ln [A]0
Let [N2O5]0 be 0.0465 M, and [N2O5]t be the concentration after 3.00 hr. Because the rate constant is expressed using seconds, 3.0 hr must be converted to seconds, which is 3.00 x 3600 s = 10800 s. the Substituting these and k = 3.4 x 10-6/s into the first-order rate equation gives:
ln [N2O5]t = -3.4 x 10-6/s x 10800 s + ln (0.0465)
ln [N2O5]t = -0.03672 – 3.07
ln [N2O5]t = -3.105
[N2O5]t = e-3.105 = 0.0448 M
The following decomposition of phosphorus pentachloride (PCl5) was found to be a first-order reaction:
PCl5(g) → PCl3(g) + 6Cl2(g)
The half-life of the reaction is 48.0 s at a certain temperature. Calculate (a) the first-order rate constant for the reaction and (b) the time required for 75 percent of the phosphorus pentachloride to decompose.
(a) k = 0.0144 s-1
(b) t = 96.3 s
For a first-order reaction, we only need the half-life to calculate the rate constant. For this, the following equation is used:
\[{t_{{\rm{1/2}}}}\;{\rm{ = }}\;\frac{{{\rm{0}}{\rm{.693}}}}{{\rm{k}}}\]
\[k\;{\rm{ = }}\;\frac{{{\rm{0}}{\rm{.693}}}}{{{t_{{\rm{1/2}}}}}}\]
\[k\;{\rm{ = }}\;\frac{{{\rm{0}}{\rm{.693}}}}{{{\rm{48}}{\rm{.0}}\;{\rm{s}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.0144}}\;{{\rm{s}}^{{\rm{ – 1}}}}\]
The integrated rate law for first-order reactions can be written as:
ln [A]t = -kt + ln [A]0
What we need to do is replace the [A]t in terms of [A]0 and solve the equation for the t. If 75% of PCl5 has decomposed, 25% of it must be remaining. So we can replace [A]t with 0.25 [A]0
ln 0.25 [A]0 = -kt + ln [A]0
ln 0.25 [A]0 – ln [A]0 = -kt
ln (0.25 [A]0 / ln [A]0) = -kt
ln (0.25) = – kt
t = ln (0.25) /-k
t = ln (0.25) /-0.0144 s-1
t = 96.3 s
The following data were collected for the decomposition reaction of hydrogen peroxide:
2H2O2(g) → 2H2O(g) + O2(g)
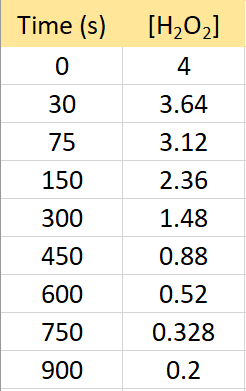
Determine rate law, the integrated rate law, and calculate the value of the rate constant.
First-order reaction, so the integrated rate law is:
ln [A]t = -kt + ln [A]0
The rate law is rate = k[H2O2]
k = 0.0033/s
If you are given data for the concentration change in time, you can determine reaction order by making graphs with a plot of a form of concentration vs time. A form of concentration means not necessarily the concentration itself, but perhaps ln[A], or the reciprocal (1/[A])of the concentration.
The important thing here is to remember that depending on the reaction order, a straight line must be obtained when [A], ln[A], or 1/[A] is plotted vs time. This is because the integrated rate laws are in the form of an equation for a straight line.
The plot of [A] vs time, does not give a straight line which excludes a zero-order reaction.
The plot of ln [A] vs time gives a straight line, and therefore, it is a first-order reaction:
ln [A]t = -kt + ln [A]0
y = mx + b
And just to demonstrate that it is not a second-order reaction, we can also plot 1/[H2O2] vs time:
The rate constant is the -slope (k = 0.0033/s) of the graph, which can be obtained from excel or calculated by Δy/Δx. We will do an example of calculating the slope in the next problem. We know the units of k because we know the order of the reaction. For a first-order reaction, it is s-1.
The rate law of this reaction will be:
rate = k[H2O2]
In a laboratory experiment, the following kinetics data for the concentration of compound A versus time were collected:
A(g) → B(g) + C(g)
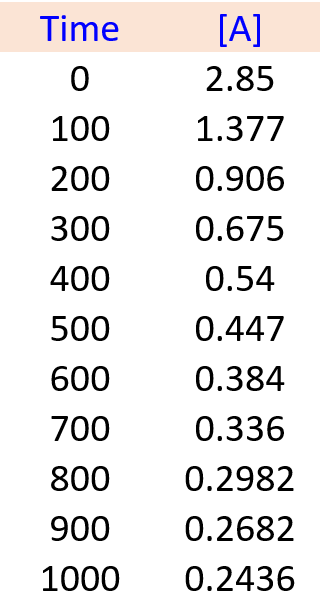
Determine the order of the reaction and the value of the rate constant. Predict the concentration of A at 450 s.
a) The reaction is second order
b) k = 0.0038 M-1 ⋅ s-1
c) [A]t = 0.485 M
The plot of [A] vs time, does not give a straight line which excludes a zero-order reaction.
The plot of ln [A] vs time, does not give a straight line either, and therefore, it is not a first-order reaction:
ln [A]t = -kt + ln [A]0
y = mx + b
A straight line is obtained when 1/[A] is plotted vs time, indicating a second-order reaction:
\[\frac{{\rm{1}}}{{{{\left[ {\rm{A}} \right]}_t}}}\; = \;kt\; + \;\frac{{\rm{1}}}{{{{\left[ {\rm{A}} \right]}_0}}}\]
y = mx + b
The rate constant is the slope of the graph, which can be obtained from excel or calculated by Δy/Δx. According to excel, k = 0.0038, so let’s confirm this by picking two y and two x values from the graph. Let’s do this for the time interval 200-600 s, since it is relatively easy to see the y values for these points. When x = 200, y = 1.1, when x = 600, y = 2.6. The rate constant then is:
k = (2.6-1.1)/(600-200) = 0.00375, which is very close to the value in excel.
So, so far we have answered two questions;
a) The reaction is second order, b) k = 0.0038 M-1 ⋅ s-1
To calculate the concentration of A at450. s., we need to use integrated rate law for second-order reactions:
\[\frac{{\rm{1}}}{{{{\left[ {\rm{A}} \right]}_t}}}\; = \;kt\; + \;\frac{{\rm{1}}}{{{{\left[ {\rm{A}} \right]}_0}}}\]
\[\frac{{\rm{1}}}{{{{\left[ {\rm{A}} \right]}_t}}}\; = \;{\rm{0}}{\rm{.0038}}\;{{\rm{M}}^{{\rm{ – 1}}}}{{\rm{s}}^{{\rm{ – 1}}}}\;{\rm{ \times }}\;{\rm{450}}{\rm{.}}\;{\rm{s}}\;{\rm{ + }}\;\frac{{\rm{1}}}{{{\rm{2}}{\rm{.85}}\;{\rm{M}}}}\]
[A]t = 0.485 M
This number makes sense, becasue according to the table givenin the problem, the concentration of A at 400 s is 0.54 M, and at 500 s, it is 0.447 M. So, at 450 s, the concentration must be between 0.54 M and 0.447 M.