In a chemical reaction, stoichiometry shows the mole-ratio of the reactants and products based on the coefficients which are written before them. It allows calculating the amount of any component of a chemical reaction if one of them is given using the mole method.
A chemical equation can be interpreted at molecular and molar levels. For example, the following equation shows the combustion reaction of ethanol (C2H5OH) producing carbon dioxide (CO2) and water (H2O):
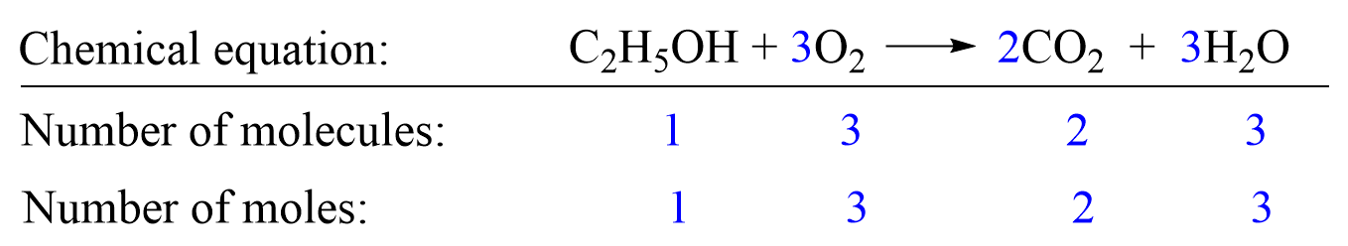
Molar level: The coefficients in blue indicate, for example, that 1 mole of C2H5OH reacts with 3 moles of O2 producing 2 moles of CO2 and 3 moles of H2O.
At the molecular level, it tells us that 1 molecule of C2H5OH reacts with 3 molecules of O2 producing 2 molecules of CO2 and 3 molecules of H2O.
So, the coefficients show the ratio of the reaction components which is like the recipe of the reaction. However, we can have any number of moles of reactants, and, using stoichiometry (the ratio of the components), we can calculate how much products can be obtained.
For example, let’s determine how much CO2 will be formed from 3.0 moles of C2H5OH by the following combustion reaction:
C2H5OH + 3O2 → 2CO2 + 3H2O
The first thing is to set up the conversion factors correlating the two components – the one with the known amount and the target which we need to determine. This is done using the coefficients in the chemical equation which indicate that 1 mole of C2H5OH produces 2 moles of CO2. Conversion factors are the two ratio fractions of these coefficients:
C2H5OH + 3O2 → 2CO2 + 3H2O
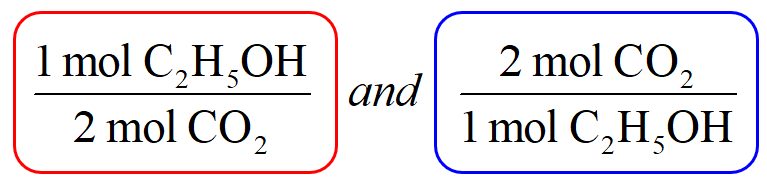
Now, because you are asked to determine the amount of CO2, pick the conversion factor such that C2H5OH is the denominator and can be canceled:
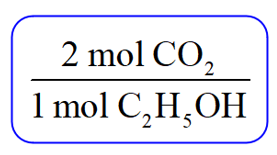
Next, write the moles of C2H5OH that are reacted (not the coefficient) and multiply it with this conversion factor:
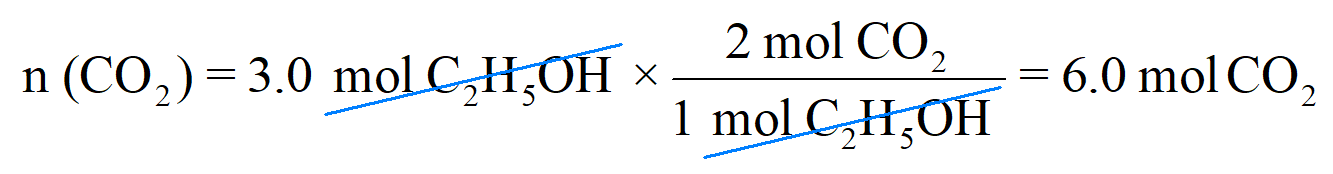
Therefore, 3.0 mol C2H5OH will produce 6 mol CO2, and this makes sense because the stoichiometry of the reaction tells us that there will always be two times more CO2 produced from a given amount of C2H5OH. So, if it was, for example, 5 mol C2H5OH, 10 mol CO2 would have been produced.
Let’s look at another example, where we need to determine the amount of a reactant required to produce certain moles of a product. Remember, as long as you know the quantity of one component in the reaction, whether it is a reactant or product, you can determine the amount of any other component.
For example: How many moles of N2 must be used to produce 10 moles of NH3 according to the following chemical equation?
3H2 + N2 → 2NH3
Step 1. Write a conversion factor between N2 and NH3 such that NH3 is on the bottom and can be canceled out:
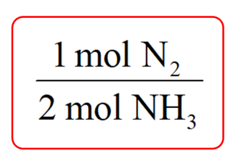
Step 2. Write the moles of ammonia (10 mol) and multiply it by the conversion factor:
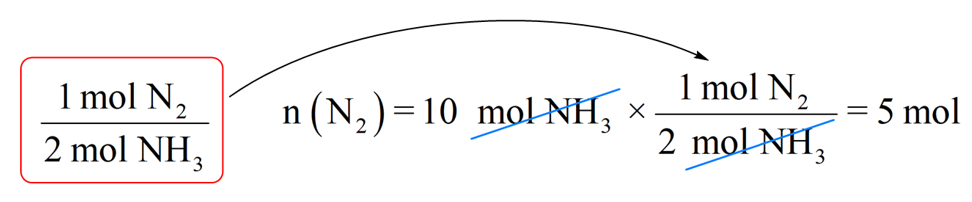
So, we will need 5 mol NH3 to produce 10 mol NH3 and this is consistent with the chemical equation which indicates that the amount of nitrogen required to produce ammonia is always two times less because of the 1:2 mole ratio.
Mass Calculations using Reaction Stoichiometry
Sometimes, or perhaps more often than not, the amounts of reaction components are given in grams or any other units. Remember, you will always need to convert them to moles first and then use the conversion factors to do the necessary calculations. This is, again, because chemical equations tell us the mole-ratio of the components by based on their coefficients.
For example: How many grams of Ba(NO3)2 can be prepared by reacting 16.5 g of HNO3 with an excess of Ba(OH)2?
Ba(OH)2 + 2HNO3 → Ba(NO3)2 + 2H2O
The plan would be to calculate the moles of HNO3, then use the mole-ratio to determine the moles of Ba(NO3)2, and finally, convert the moles to the mass of Ba(NO3)2:
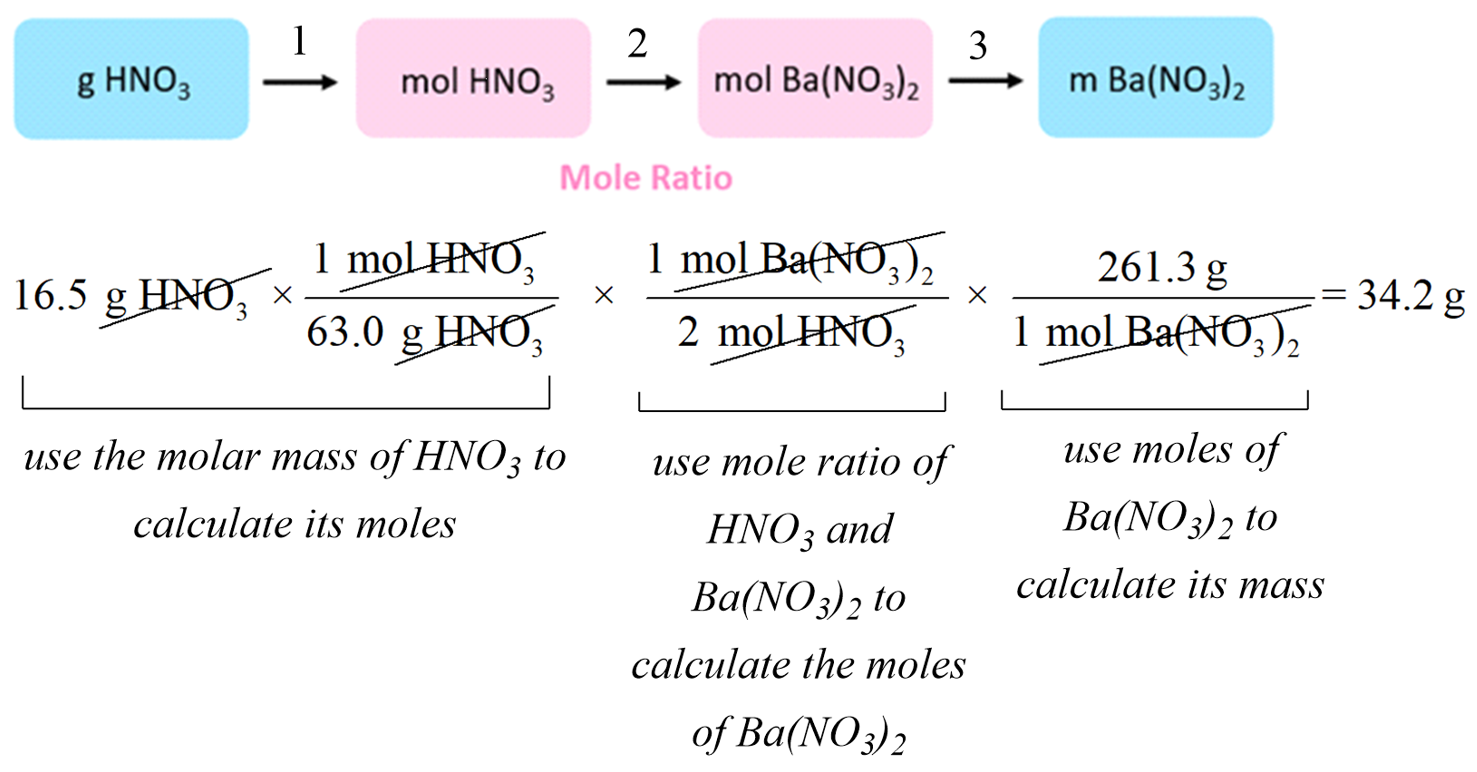
You can also do this step-by-step to better follow the entire calculation:
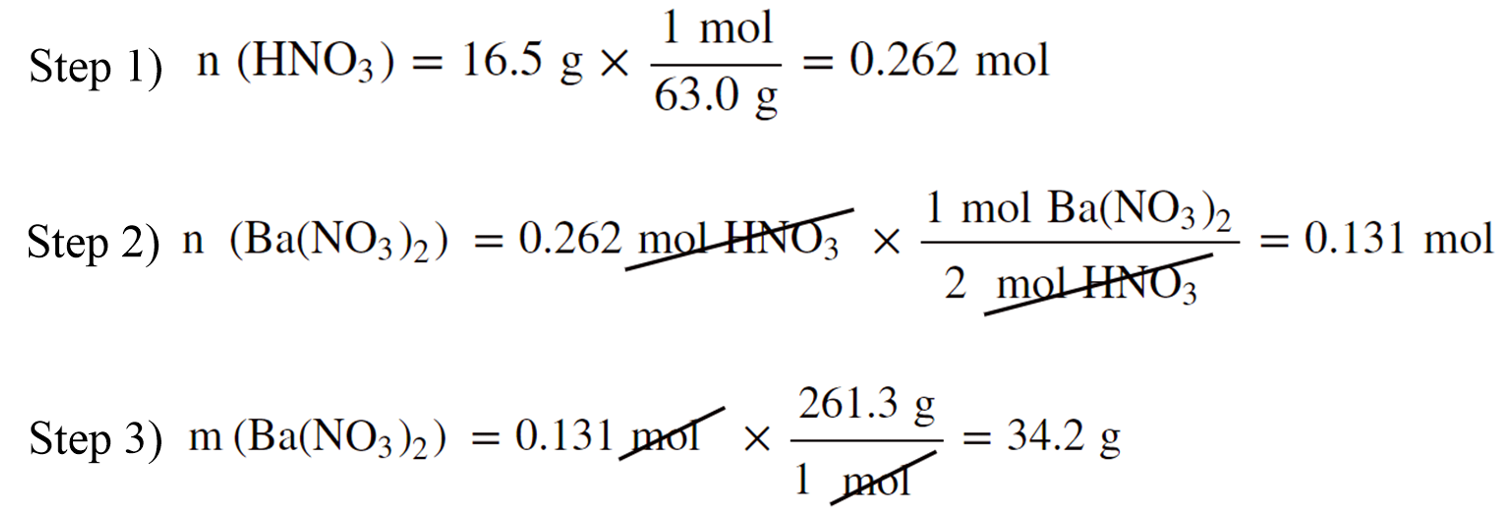
Practice
Consider the balanced equation:
C5H12 + 8 O2 → 5CO2 + 6H2O
Complete the table showing the appropriate number of moles of reactants and products.
| mol C5H12 | mol O2 | mol CO2 | mol H2O |
| 2 | |||
| 2.5 | |||
| 3 | |||
| 5.4 |
C5H12 + 8 O2 → 5CO2 + 6H2O
| mol C5H12 | mol O2 | mol CO2 | mol H2O |
| 2 | 16 | 10 | 12 |
| 0.3125 | 2.5 | 1.5625 | 1.875 |
| 0.6 | 4.8 | 3 | 3.6 |
| 0.9 | 7.2 | 4.5 | 5.4 |
The moles of other molecules are calculated based on the stoichiometric ratio. For the first row the moles are calculated as follows:
\[{\rm{n}}\left( {{{\rm{O}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{2 }}\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}}}\;{\rm{ \times }}\;\frac{{{\rm{8}}\;{\rm{mol}}\;{{\rm{O}}_{\rm{2}}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}}}}}\;{\rm{ = }}\;{\rm{16}}\;{\rm{mol}}\]
\[{\rm{n}}\left( {{\rm{C}}{{\rm{O}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{2 }}\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}}}\;{\rm{ \times }}\;\frac{{{\rm{5}}\;{\rm{mol}}\;C{{\rm{O}}_{\rm{2}}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}}}}}\;{\rm{ = }}\;{\rm{10}}\;{\rm{mol}}\]
\[{\rm{n}}\left( {{{\rm{H}}_{\rm{2}}}{\rm{O}}} \right)\;{\rm{ = }}\;{\rm{2 }}\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}}}\;{\rm{ \times }}\;\frac{{{\rm{6}}\;{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}{\rm{O}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}}}}}\;{\rm{ = }}\;{\rm{12}}\;{\rm{mol}}\]
For the second row:
\[{\rm{n}}\left( {{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}} \right)\;{\rm{ = }}\;{\rm{2}}{\rm{.5 }}\cancel{{{\rm{mol}}\;{{\rm{O}}_{\rm{2}}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}\;{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}}}{{8\;\cancel{{{\rm{mol}}\;{{\rm{O}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.3125}}\;{\rm{mol}}\]
\[{\rm{n}}\left( {{\rm{C}}{{\rm{O}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{2}}{\rm{.5 }}\cancel{{{\rm{mol}}\;{{\rm{O}}_{\rm{2}}}}}\;{\rm{ \times }}\;\frac{{{\rm{5}}\;{\rm{mol}}\;{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}}}{{{\rm{8}}\;\cancel{{{\rm{mol}}\;{{\rm{O}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{1}}{\rm{.5625}}\;{\rm{mol}}\]
\[{\rm{n}}\left( {{{\rm{H}}_{\rm{2}}}{\rm{O}}} \right)\;{\rm{ = }}\;{\rm{2}}{\rm{.5 }}\cancel{{{\rm{mol}}\;{{\rm{O}}_{\rm{2}}}}}\;{\rm{ \times }}\;\frac{{{\rm{6}}\;{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}{\rm{O}}}}{{{\rm{8}}\;\cancel{{{\rm{mol}}\;{{\rm{O}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{1}}{\rm{.875}}\;{\rm{mol}}\]
For the third row:
\[{\rm{n}}\left( {{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}} \right)\;{\rm{ = }}\;{\rm{3 }}\cancel{{{\rm{mol}}\;{\rm{C}}{{\rm{O}}_{\rm{2}}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}\;{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}}}{{{\rm{5}}\;\cancel{{{\rm{mol}}\;{\rm{C}}{{\rm{O}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.6}}\;{\rm{mol}}\]
\[{\rm{n}}\left( {{{\rm{O}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{3 }}\cancel{{{\rm{mol}}\;{\rm{C}}{{\rm{O}}_{\rm{2}}}}}\;{\rm{ \times }}\;\frac{{{\rm{8}}\;{\rm{mol}}\;{{\rm{O}}_{\rm{2}}}}}{{{\rm{5}}\;\cancel{{{\rm{mol}}\;{\rm{C}}{{\rm{O}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{4}}{\rm{.8}}\;{\rm{mol}}\]
\[{\rm{n}}\left( {{{\rm{H}}_{\rm{2}}}{\rm{O}}} \right)\;{\rm{ = }}\;{\rm{3 }}\cancel{{{\rm{mol}}\;{\rm{C}}{{\rm{O}}_{\rm{2}}}}}\;{\rm{ \times }}\;\frac{{{\rm{6}}\;{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}{\rm{O}}}}{{{\rm{5}}\;\cancel{{{\rm{mol}}\;{\rm{C}}{{\rm{O}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{3}}{\rm{.6}}\;{\rm{mol}}\]
For the fourth row:
\[{\rm{n}}\left( {{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}} \right)\;{\rm{ = }}\;{\rm{5}}{\rm{.4 }}\cancel{{{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}{\rm{O}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}\;{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}}}{{{\rm{6}}\;\cancel{{{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}{\rm{O}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.9}}\;{\rm{mol}}\]
\[{\rm{n}}\left( {{{\rm{O}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{5}}{\rm{.4 }}\cancel{{{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}{\rm{O}}}}\;{\rm{ \times }}\;\frac{{{\rm{8}}\;{\rm{mol}}\;{{\rm{O}}_{\rm{2}}}}}{{{\rm{6}}\;\cancel{{{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}{\rm{O}}}}}}\;{\rm{ = }}\;{\rm{7}}{\rm{.2}}\;{\rm{mol}}\]
\[{\rm{n}}\left( {{\rm{C}}{{\rm{O}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{5}}{\rm{.4 }}\cancel{{{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}{\rm{O}}}}\;{\rm{ \times }}\;\frac{{{\rm{5}}\;{\rm{mol}}\;{\rm{C}}{{\rm{O}}_{\rm{2}}}}}{{{\rm{6}}\;\cancel{{{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}{\rm{O}}}}}}\;{\rm{ = }}\;{\rm{4}}{\rm{.5}}\;{\rm{mol}}\]
How many grams of CO2 and H2O are produced from the combustion of 220. g of propane (C3H8)?
C3H8(g) + 5O2(g) → 3CO2(g) + 4H2O(g)
660. g CO2
360. g H2O
The amount of product, for a given amount of reactant, is calculated based on their molar/stoichiometric ratio. So, the first step is to determine the moles of propane. The overall plan is:
The moles of C3H8 are calculated using its molar mass:
\[{\rm{n(}}{{\rm{C}}_{\rm{3}}}{{\rm{H}}_{\rm{8}}}{\rm{)}}\;{\rm{ = }}\;{\rm{220}}{\rm{.5}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{44}}{\rm{.1}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{5}}{\rm{.00}}\;{\rm{mol}}\]
Next, we find the moles of CO2 based on its molar ratio with C3H8:
\[{\rm{n}}\left( {{\rm{C}}{{\rm{O}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{5}}{\rm{.00 }}\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{3}}}{{\rm{H}}_{\rm{8}}}}}\;{\rm{ \times }}\;\frac{{{\rm{3}}\;{\rm{mol}}\;{\rm{C}}{{\rm{O}}_{\rm{2}}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{3}}}{{\rm{H}}_{\rm{8}}}}}}}\;{\rm{ = }}\;{\rm{15}}{\rm{.0}}\;{\rm{mol}}\]
And finally, the mass of the CO2 is determined using its moles and molar mass:
\[{\rm{m}}\left( {{\rm{C}}{{\rm{O}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{15}}{\rm{.0 }}\cancel{{{\rm{mol}}\;}}\;{\rm{ \times }}\;\frac{{{\rm{44}}{\rm{.0}}\;{\rm{g}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;}}}}\;{\rm{ = }}\;{\rm{660}}{\rm{.}}\;{\rm{g}}\]
Follow the same procedure to find the mass of H2O:
\[{\rm{n}}\left( {{{\rm{H}}_{\rm{2}}}{\rm{O}}} \right)\;{\rm{ = }}\;{\rm{5}}{\rm{.00 }}\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{3}}}{{\rm{H}}_{\rm{8}}}}}\;{\rm{ \times }}\;\frac{{{\rm{4}}\;{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}{\rm{O}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{3}}}{{\rm{H}}_{\rm{8}}}}}}}\;{\rm{ = }}\;{\rm{20}}{\rm{.0}}\;{\rm{mol}}\]
\[{\rm{m}}\left( {{{\rm{H}}_{\rm{2}}}{\rm{O}}} \right)\;{\rm{ = }}\;{\rm{20}}{\rm{.0 }}\cancel{{{\rm{mol}}\;}}\;{\rm{ \times }}\;\frac{{{\rm{18}}{\rm{.0}}\;{\rm{g}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;}}}}\;{\rm{ = }}\;{\rm{360}}{\rm{.}}\;{\rm{g}}\]
How many grams of CaCl2 can be produced from 65.0 g of Ca(OH)2 according to the following reaction,
Ca(OH)2 + 2HCl → CaCl2 + 2H2O
97.3 g
Here is the conceptual plan for solving this problem:
The moles of Ca(OH)2 are calculated using its molar mass:
\[{\rm{n}}\;{\rm{(Ca}}{\left( {{\rm{OH}}} \right)_{\rm{2}}}{\rm{)}}\;{\rm{ = }}\;{\rm{65}}{\rm{.0}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{74}}{\rm{.1}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.877}}\;{\rm{mol}}\]
Next, we find the moles of CaCl2 based on its molar ratio with Ca(OH)2:
\[{\rm{n}}\;\left( {{\rm{CaC}}{{\rm{l}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.877 }}\cancel{{{\rm{mol}}\;{\rm{Ca}}{{\left( {{\rm{OH}}} \right)}_{\rm{2}}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}\;{\rm{CaC}}{{\rm{l}}_{\rm{2}}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{Ca}}{{\left( {{\rm{OH}}} \right)}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.877}}\;{\rm{mol}}\]
Notice that moles of CaCl2 are equal to the moles of Ca(OH)2. This is because of their 1:1 molar ratio in the equation.
The last step is converting the moles to mass of the CaCl2:
\[{\rm{m}}\left( {{\rm{CaC}}{{\rm{l}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.877 }}\cancel{{{\rm{mol}}\;}}\;{\rm{ \times }}\;\frac{{{\rm{111}}\;{\rm{g}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;}}}}\;{\rm{ = }}\;{\rm{97}}{\rm{.3}}\;{\rm{g}}\]
This process can, and often is shown as a one-step conversion as we do in dimensional analysis. It would be as follows:
\[{\rm{m}}\left( {{\rm{CaC}}{{\rm{l}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{65}}{\rm{.0}}\;{\cancel{{{\rm{g}}\;{\rm{Ca}}{{\left( {{\rm{OH}}} \right)}_{\rm{2}}}}}_{\rm{\;}}}{\rm{ \times }}\;\frac{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{Ca}}{{\left( {{\rm{OH}}} \right)}_{\rm{2}}}}}}}{{{\rm{74}}{\rm{.1}}\;\cancel{{{\rm{g}}\;{\rm{Ca}}{{\left( {{\rm{OH}}} \right)}_{\rm{2}}}}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{CaC}}{{\rm{l}}_{\rm{2}}}}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{Ca}}{{\left( {{\rm{OH}}} \right)}_{\rm{2}}}}}}}\; \times \;\frac{{{\rm{111}}\;{\rm{g}}\;{\rm{CaC}}{{\rm{l}}_{\rm{2}}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{CaC}}{{\rm{l}}_{\rm{2}}}\;}}}}\;\;{\rm{ = }}\;{\rm{97}}{\rm{.3}}\;{\rm{g}}\]
This method is completely fine, however, I prefer doing these conversions stepwise to better see what happens in each step, and therefore, most exercises will be solved by doing one conversion at a time.
How many moles of oxygen are formed when 75.0 g of Cu(NO3)2 decomposes according to the following reaction?
2Cu(NO3)2 → 2CuO + 4NO2 + O2
0.200 mol
The amount of product, for a given amount of reactant, is calculated based on their molar/stoichiometric ratio.
So, the conceptual plan is:
\[{\rm{n}}\;{\rm{(Cu}}{\left( {{\rm{N}}{{\rm{O}}_{\rm{3}}}} \right)_{\rm{2}}}{\rm{\;)}}\;{\rm{ = }}\;{\rm{75}}{\rm{.0}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{187}}{\rm{.5}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.400}}\;{\rm{mol}}\]
\[{\rm{n}}\;\left( {{{\rm{O}}_{{\rm{2\;}}}}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.400}}\;\cancel{{{\rm{mol}}\;{\rm{Cu}}{{\left( {{\rm{N}}{{\rm{O}}_{\rm{3}}}} \right)}_{\rm{2}}}{\rm{\;}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}\;{{\rm{O}}_{\rm{2}}}}}{{\cancel{{{\rm{2}}\;{\rm{mol}}\;{\rm{Cu}}{{\left( {{\rm{N}}{{\rm{O}}_{\rm{3}}}} \right)}_{\rm{2}}}{\rm{\;}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.200}}\;{\rm{mol}}\]
How many grams of MnCl2 can be prepared from 52.1 grams of MnO2?
MnO2 + 4HCl → MnCl2 + Cl2 + 2H2O
75.5 g
The amount of product, for a given amount of reactant, is calculated based on their molar/stoichiometric ratio. So, the first step is to determine the moles of propane. The overall plan is:
The moles of MnO2 are calculated using its molar mass:
\[{\rm{n}}\;{\rm{(Mn}}{{\rm{O}}_{\rm{2}}}{\rm{)}}\;{\rm{ = }}\;{\rm{52}}{\rm{.1}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{86}}{\rm{.9}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.600}}\;{\rm{mol}}\]
Next, we find the moles of MnCl2 based on its molar ratio with MnO2:
\[{\rm{n}}\;\left( {{\rm{MnC}}{{\rm{l}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.600 }}\cancel{{{\rm{mol}}\;{\rm{Mn}}{{\rm{O}}_{\rm{2}}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}\;{\rm{MnC}}{{\rm{l}}_{\rm{2}}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{Mn}}{{\rm{O}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.600}}\;{\rm{mol}}\]
And finally, the mass of the MnCl2 is determined using its moles and molar mass:
\[{\rm{m}}\left( {{\rm{MnC}}{{\rm{l}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.600 }}\cancel{{{\rm{mol}}\;}}\;{\rm{ \times }}\;\frac{{{\rm{125}}{\rm{.8}}\;{\rm{g}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;}}}}\;{\rm{ = }}\;{\rm{75}}{\rm{.5g}}\]
Determine the mass of oxygen that is formed when an 18.3-g sample of potassium chlorate is decomposed according to the following equation:
2KClO3(s) → 2KCl(s) + 3O2(g).
7.16 g
The amount of product, for a given amount of reactant, is calculated based on their molar/stoichiometric ratio. So, the first step is to determine the moles of propane. The conceptual plan is:
The moles of MnO2 are calculated using its molar mass:
\[{\rm{n}}\;{\rm{(KCl}}{{\rm{O}}_{\rm{3}}}{\rm{)}}\;{\rm{ = }}\;{\rm{18}}{\rm{.3}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{122}}{\rm{.6}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.149}}\;{\rm{mol}}\]
Next, we find the moles of O2 based on its molar ratio with KClO3:
\[{\rm{n}}\;\left( {{{\rm{O}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.149 }}\cancel{{{\rm{mol}}\;{\rm{KCl}}{{\rm{O}}_{\rm{3}}}}}\;{\rm{ \times }}\;\frac{{{\rm{3}}\;{\rm{mol}}\;{{\rm{O}}_{\rm{2}}}}}{{{\rm{2}}\;\cancel{{{\rm{mol}}\;{\rm{KCl}}{{\rm{O}}_{\rm{3}}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.224}}\;{\rm{mol}}\]
And finally, the mass of the MnCl2 is determined using its moles and molar mass:
\[{\rm{m}}\left( {{{\rm{O}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.224 }}\cancel{{{\rm{mol}}\;}}\;{\rm{ \times }}\;\frac{{{\rm{32}}{\rm{.0}}\;{\rm{g}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;}}}}\;{\rm{ = }}\;{\rm{7}}{\rm{.16}}\;{\rm{g}}\]
How many grams of H2O will be formed when 48.0 grams H2 are mixed with excess hydrogen gas?
2H2 + O2 → 2H2O
432 g
The amount of product, for a given amount of reactant, is calculated based on their molar/stoichiometric ratio. So, the first step is to determine the moles of propane. The conceptual plan is:
The moles of H2O are calculated using its molar mass:
\[{\rm{n}}\;{\rm{(}}{{\rm{H}}_2}{\rm{)}}\;{\rm{ = }}\;{\rm{48}}{\rm{.0}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{2}}{\rm{.00}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{24}}{\rm{.0}}\;{\rm{mol}}\]
Next, we find the moles of H2O based on its molar ratio with H2:
\[{\rm{n}}\;\left( {{{\rm{H}}_{\rm{2}}}{\rm{O}}} \right)\;{\rm{ = }}\;{\rm{24}}{\rm{.0 }}\cancel{{{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}}}\;{\rm{ \times }}\;\frac{{{\rm{2}}\;{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}{\rm{O}}}}{{{\rm{2}}\;\cancel{{{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{24}}{\rm{.0}}\;{\rm{mol}}\]
And finally, the mass of the H2O is determined using its moles and molar mass:
\[{\rm{m}}\left( {{{\rm{H}}_{\rm{2}}}{\rm{O}}} \right)\;{\rm{ = }}\;{\rm{24}}{\rm{.0 }}\cancel{{{\rm{mol}}\;}}\;{\rm{ \times }}\;\frac{{{\rm{18}}{\rm{.0}}\;{\rm{g}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;}}}}\;{\rm{ = }}\;{\rm{432}}\;{\rm{g}}\]
Consider the chlorination reaction of methane (CH4):
CH4(g) + 4Cl2(g) → CCl4(g) + 4HCl(g)
How many moles of CH4 were used in the reaction if 51.9 g of CCl4 were obtained?
0.337 mol
The amount of product, for a given amount of reactant, is calculated based on their molar/stoichiometric ratio. So, the first step is to determine the moles of propane. The conceptual plan is:
The moles of CCl4 are calculated using its molar mass:
\[{\rm{n}}\;{\rm{(CC}}{{\rm{l}}_{\rm{4}}}{\rm{)}}\;{\rm{ = }}\;{\rm{51}}{\rm{.9}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{153}}{\rm{.8}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.337}}\;{\rm{mol}}\]
Next, we find the moles of CH4 based on its molar ratio with CCl4. It is a 1:1 ratio, so there is going to be 0.337 mol CH4:
\[{\rm{n}}\;\left( {{\rm{C}}{{\rm{H}}_{\rm{4}}}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.337 }}\cancel{{{\rm{mol}}\;{\rm{CC}}{{\rm{l}}_{\rm{4}}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}\;{\rm{C}}{{\rm{H}}_{\rm{4}}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{CC}}{{\rm{l}}_{\rm{4}}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.337}}\;{\rm{mol}}\]
How many grams of Ba(NO3)2 can be produced by reacting 16.5 g of HNO3 with an excess of Ba(OH)2?
34.2 g
We need to first write the balanced chemical equation to do the calculations:
Ba(OH)2 + 2HNO3 → Ba(NO3)2 + 2H2O
The conceptual plan would be:
So, let’s start with the moles of HNO3:
\[{\rm{n}}\;{\rm{(HN}}{{\rm{O}}_{\rm{3}}}{\rm{)}}\;{\rm{ = }}\;{\rm{16}}{\rm{.5}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{63}}{\rm{.0}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.262}}\;{\rm{mol}}\]
Once we have the moles, we can determine the moles of Ba(NO3)2 based on the molar ratio, and then convert the moles to the mass:
\[{\rm{n}}\;\left( {{\rm{Ba}}{{\left( {{\rm{N}}{{\rm{O}}_{\rm{3}}}} \right)}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.262 }}\cancel{{{\rm{mol}}\;{\rm{HN}}{{\rm{O}}_{\rm{3}}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}\;{\rm{Ba}}{{\left( {{\rm{N}}{{\rm{O}}_{\rm{3}}}} \right)}_{\rm{2}}}}}{{{\rm{2}}\;\cancel{{{\rm{mol}}\;{\rm{HN}}{{\rm{O}}_{\rm{3}}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.131}}\;{\rm{mol}}\]
\[{\rm{m}}\left( {{\rm{Ba}}{{\left( {{\rm{N}}{{\rm{O}}_{\rm{3}}}} \right)}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.131 }}\cancel{{{\rm{mol}}\;}}\;{\rm{ \times }}\;\frac{{{\rm{261}}{\rm{.3}}\;{\rm{g}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;}}}}\;{\rm{ = }}\;{\rm{34}}{\rm{.2}}\;{\rm{g}}\]
Ethanol can be obtained by fermentation – a complex chemical process breaking down glucose to ethanol and carbon dioxide.
C6H12O6 → 2C2H5OH + 2CO2
glucose ethanol
How many mL of ethanol (d =0.789 g/mL) can be obtained by this process starting with 286 g of glucose?
186 mL
This problem has an additional step of converting the mass of the product to volume. Other than that, we follow the same strategy and steps as in the previous problems:
\[{\rm{n}}\;{\rm{(}}{{\rm{C}}_{\rm{6}}}{{\rm{H}}_{{\rm{12}}}}{{\rm{O}}_{\rm{6}}}{\rm{)}}\;{\rm{ = }}\;{\rm{286}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{180}}{\rm{.2}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{1}}{\rm{.59}}\;{\rm{mol}}\]
Now, we can find the moles of C2H5OH:
\[{\rm{n}}\;\left( {{{\rm{C}}_{\rm{2}}}{{\rm{H}}_{\rm{5}}}{\rm{OH}}} \right)\;{\rm{ = }}\;{\rm{1}}{\rm{.59 }}\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{6}}}{{\rm{H}}_{{\rm{12}}}}{{\rm{O}}_{\rm{6}}}}}\;{\rm{ \times }}\;\frac{{{\rm{2}}\;{\rm{mol}}\;{{\rm{C}}_{\rm{2}}}{{\rm{H}}_{\rm{5}}}{\rm{OH}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{6}}}{{\rm{H}}_{{\rm{12}}}}{{\rm{O}}_{\rm{6}}}}}}}\;{\rm{ = }}\;{\rm{3}}{\rm{.18}}\;{\rm{mol}}\]
\[{\rm{m}}\left( {{{\rm{C}}_{\rm{2}}}{{\rm{H}}_{\rm{5}}}{\rm{OH}}} \right)\;{\rm{ = }}\;{\rm{3}}{\rm{.18 }}\cancel{{{\rm{mol}}\;}}\;{\rm{ \times }}\;\frac{{{\rm{46}}{\rm{.1}}\;{\rm{g}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;}}}}\;{\rm{ = }}\;{\rm{147}}\;{\rm{g}}\]
The last step is converting the mass to volume:
\[{\rm{v}}\left( {{{\rm{C}}_{\rm{2}}}{{\rm{H}}_{\rm{5}}}{\rm{OH}}} \right)\;{\rm{ = }}\;{\rm{147}}\;\cancel{{\rm{g}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mL}}}}{{{\rm{0}}{\rm{.789}}\;\cancel{{\rm{g}}}}}\;{\rm{ = }}\;{\rm{186}}\;{\rm{mL}}\]
36.0 g of butane (C4H10) was burned in an excess of oxygen and the resulting carbon dioxide (CO2) was collected in a sealed vessel.
2C4H10 + 13O2 → 8CO2 + 10H2O
How many grams of LiOH will be necessary to consume all the CO2 from the first reaction?
2LiOH + CO2 → Li2CO3 + H2O
119 g
There are two reactions here, and the link between them is the CO2 that is formed in the first reaction and used in the second.
So, the plan would be to determine the moles of CO2 in the first reaction, and use it to calculate the moles, and consequently the mass of LiOH.
\[{\rm{n}}\;{\rm{(}}{{\rm{C}}_{\rm{4}}}{{\rm{H}}_{{\rm{10}}}}{\rm{)}}\;{\rm{ = }}\;{\rm{36}}{\rm{.0}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{58}}{\rm{.1}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.620}}\;{\rm{mol}}\]
\[{\rm{n}}\;\left( {{\rm{C}}{{\rm{O}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.620 }}\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{4}}}{{\rm{H}}_{{\rm{10}}}}}}\;{\rm{ \times }}\;\frac{{{\rm{8}}\;{\rm{mol}}\;{\rm{C}}{{\rm{O}}_{\rm{2}}}}}{{{\rm{2}}\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{4}}}{{\rm{H}}_{{\rm{10}}}}}}}}\;{\rm{ = }}\;{\rm{2}}{\rm{.48}}\;{\rm{mol}}\]
This is the amount of CO2 that will be reacted with LiOH in a 1:2 ratio. So, we can determine the moles of LiOH and convert them to the mass:
\[{\rm{n}}\;\left( {{\rm{LiOH}}} \right)\;{\rm{ = }}\;{\rm{2}}{\rm{.48 }}\cancel{{{\rm{mol}}\;{\rm{C}}{{\rm{O}}_{\rm{2}}}}}\;{\rm{ \times }}\;\frac{{{\rm{2}}\;{\rm{mol}}\;{\rm{LiOH}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{C}}{{\rm{O}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{4}}{\rm{.96}}\;{\rm{mol}}\]
\[{\rm{m}}\;\left( {{\rm{LiOH}}} \right)\;{\rm{ = }}\;{\rm{4}}{\rm{.96}}\;\cancel{{{\rm{mol}}\;{\rm{LiOH}}}}\;{\rm{ \times }}\;\frac{{{\rm{24}}{\rm{.0}}\;{\rm{g}}\;{\rm{LiOH}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{LiOH}}}}}}\;{\rm{ = }}\;{\rm{119}}\;{\rm{g}}\;\]
Hi, for #8 in the practice questions. The question asks for the mass of CCl4, but the work was only done to solve for the moles of CCl4.
Oh, thanks. The question was supposed to be rephrased.
No problem!
For #9, there’s no reaction unless I took a peak at the solution. Therefore, this problem is unsolvable.
Some problems are going to require predicting the product of the reaction first. This is usually covered in the next chapter (chapter 4 in most textbooks). Check the following two posts for the principles of predicting the product of chemical reactions:
Predicting The Products of Chemical Reactions
Acid-Base Reactions