This is a comprehensive, end-of-chapter set of practice problems on stoichiometry that covers balancing chemical equations, mole-ratio calculations, limiting reactants, and percent yield concepts.
The links to the corresponding topics are given below.
Practice
Balance the following chemical equations:
a) HCl + O2 → H2O + Cl2
b) Al(NO3)3 + NaOH → Al(OH)3 + NaNO3
c) H2 + N2 → NH3
d) PCl5 + H2O → H3PO4 + HCl
e) Fe + H2SO4 → Fe2(SO4)3 + H2
f) CaCl2 + HNO3 → Ca(NO3)2 + HCl
g) KO2 + H2O → KOH + O2 + H2O2
h) Al + H2O → Al2O3 + H2
i) Fe + Br2 → FeBr3
j) Cu + HNO3 → Cu(NO3)2 + NO2 + H2O
k) Al(OH)3 → Al2O3 + H2O
l) NH3 + O2 → NO + H2O
m) Ca(AlO2)2 + HCl → AlCl3 + CaCl2 + H2O
n) C5H12 + O2 → CO2 + H2O
o) P4O10 + H2O → H3PO4
p) Na2CrO4 + Pb(NO3)2 → PbCrO4 + NaNO3
q) MgCl2 + AgNO3 → AgCl + Mg(NO3)2
r) KClO3 → KClO4 + KCl
s) Ca(OH)2 + H3PO4 → Ca3(PO4)2 + H2O
4HCl + O2 → 2H2O + 2Cl2
Al(NO3)3 + 3NaOH → Al(OH)3 + 3NaNO3
3H2 + N2 → 2NH3
PCl5 + 4H2O → H3PO4 + 5HCl
2Fe + 3H2SO4 → Fe2(SO4)3 + 3H2
CaCl2 + 2HNO3 → Ca(NO3)2 + 2HCl
2KO2 + 2H2O → 2KOH + O2 + H2O2
2Al + 3H2O → Al2O3 + 3H2
2Fe + 3Br2 → 2FeBr3
Cu + 4HNO3 → Cu(NO3)2 + 2NO2 + 2H2O
2Al(OH)3 → Al2O3 + 3H2O
4NH3 + 5O2 → 4NO + 6H2O
Ca(AlO2)2 + 8HCl → 2AlCl3 + CaCl2 + 4H2O
C5H12 + 8 O2 → 5CO2 + 6H2O
P4O10 + 6H2O → 4H3PO4
Na2CrO4 + Pb(NO3)2 → PbCrO4 + 2NaNO3
MgCl2 + 2AgNO3 → 2AgCl + Mg(NO3)2
4KClO3 → 3KClO4 + KCl
3Ca(OH)2 + 2H3PO4 → Ca3(PO4)2 + 6H2O
Consider the balanced equation:
C5H12 + 8 O2 → 5CO2 + 6H2O
Complete the table showing the appropriate number of moles of reactants and products.
| mol C5H12 | mol O2 | mol CO2 | mol H2O |
| 2 | |||
| 2.5 | |||
| 3 | |||
| 5.4 |
C5H12 + 8 O2 → 5CO2 + 6H2O
| mol C5H12 | mol O2 | mol CO2 | mol H2O |
| 2 | 16 | 10 | 12 |
| 0.3125 | 2.5 | 1.5625 | 1.875 |
| 0.6 | 4.8 | 3 | 3.6 |
| 0.9 | 7.2 | 4.5 | 5.4 |
The moles of other molecules are calculated based on the stoichiometric ratio. For the first row the moles are calculated as follows:
\[{\rm{n}}\left( {{{\rm{O}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{2 }}\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}}}\;{\rm{ \times }}\;\frac{{{\rm{8}}\;{\rm{mol}}\;{{\rm{O}}_{\rm{2}}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}}}}}\;{\rm{ = }}\;{\rm{16}}\;{\rm{mol}}\]
\[{\rm{n}}\left( {{\rm{C}}{{\rm{O}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{2 }}\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}}}\;{\rm{ \times }}\;\frac{{{\rm{5}}\;{\rm{mol}}\;C{{\rm{O}}_{\rm{2}}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}}}}}\;{\rm{ = }}\;{\rm{10}}\;{\rm{mol}}\]
\[{\rm{n}}\left( {{{\rm{H}}_{\rm{2}}}{\rm{O}}} \right)\;{\rm{ = }}\;{\rm{2 }}\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}}}\;{\rm{ \times }}\;\frac{{{\rm{6}}\;{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}{\rm{O}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}}}}}\;{\rm{ = }}\;{\rm{12}}\;{\rm{mol}}\]
For the second row:
\[{\rm{n}}\left( {{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}} \right)\;{\rm{ = }}\;{\rm{2}}{\rm{.5 }}\cancel{{{\rm{mol}}\;{{\rm{O}}_{\rm{2}}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}\;{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}}}{{8\;\cancel{{{\rm{mol}}\;{{\rm{O}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.3125}}\;{\rm{mol}}\]
\[{\rm{n}}\left( {{\rm{C}}{{\rm{O}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{2}}{\rm{.5 }}\cancel{{{\rm{mol}}\;{{\rm{O}}_{\rm{2}}}}}\;{\rm{ \times }}\;\frac{{{\rm{5}}\;{\rm{mol}}\;{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}}}{{{\rm{8}}\;\cancel{{{\rm{mol}}\;{{\rm{O}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{1}}{\rm{.5625}}\;{\rm{mol}}\]
\[{\rm{n}}\left( {{{\rm{H}}_{\rm{2}}}{\rm{O}}} \right)\;{\rm{ = }}\;{\rm{2}}{\rm{.5 }}\cancel{{{\rm{mol}}\;{{\rm{O}}_{\rm{2}}}}}\;{\rm{ \times }}\;\frac{{{\rm{6}}\;{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}{\rm{O}}}}{{{\rm{8}}\;\cancel{{{\rm{mol}}\;{{\rm{O}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{1}}{\rm{.875}}\;{\rm{mol}}\]
For the third row:
\[{\rm{n}}\left( {{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}} \right)\;{\rm{ = }}\;{\rm{3 }}\cancel{{{\rm{mol}}\;{\rm{C}}{{\rm{O}}_{\rm{2}}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}\;{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}}}{{{\rm{5}}\;\cancel{{{\rm{mol}}\;{\rm{C}}{{\rm{O}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.6}}\;{\rm{mol}}\]
\[{\rm{n}}\left( {{{\rm{O}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{3 }}\cancel{{{\rm{mol}}\;{\rm{C}}{{\rm{O}}_{\rm{2}}}}}\;{\rm{ \times }}\;\frac{{{\rm{8}}\;{\rm{mol}}\;{{\rm{O}}_{\rm{2}}}}}{{{\rm{5}}\;\cancel{{{\rm{mol}}\;{\rm{C}}{{\rm{O}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{4}}{\rm{.8}}\;{\rm{mol}}\]
\[{\rm{n}}\left( {{{\rm{H}}_{\rm{2}}}{\rm{O}}} \right)\;{\rm{ = }}\;{\rm{3 }}\cancel{{{\rm{mol}}\;{\rm{C}}{{\rm{O}}_{\rm{2}}}}}\;{\rm{ \times }}\;\frac{{{\rm{6}}\;{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}{\rm{O}}}}{{{\rm{5}}\;\cancel{{{\rm{mol}}\;{\rm{C}}{{\rm{O}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{3}}{\rm{.6}}\;{\rm{mol}}\]
For the fourth row:
\[{\rm{n}}\left( {{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}} \right)\;{\rm{ = }}\;{\rm{5}}{\rm{.4 }}\cancel{{{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}{\rm{O}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}\;{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}}}{{{\rm{6}}\;\cancel{{{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}{\rm{O}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.9}}\;{\rm{mol}}\]
\[{\rm{n}}\left( {{{\rm{O}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{5}}{\rm{.4 }}\cancel{{{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}{\rm{O}}}}\;{\rm{ \times }}\;\frac{{{\rm{8}}\;{\rm{mol}}\;{{\rm{O}}_{\rm{2}}}}}{{{\rm{6}}\;\cancel{{{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}{\rm{O}}}}}}\;{\rm{ = }}\;{\rm{7}}{\rm{.2}}\;{\rm{mol}}\]
\[{\rm{n}}\left( {{\rm{C}}{{\rm{O}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{5}}{\rm{.4 }}\cancel{{{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}{\rm{O}}}}\;{\rm{ \times }}\;\frac{{{\rm{5}}\;{\rm{mol}}\;{\rm{C}}{{\rm{O}}_{\rm{2}}}}}{{{\rm{6}}\;\cancel{{{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}{\rm{O}}}}}}\;{\rm{ = }}\;{\rm{4}}{\rm{.5}}\;{\rm{mol}}\]
How many grams of CO2 and H2O are produced from the combustion of 220. g of propane (C3H8)?
C3H8(g) + 5O2(g) → 3CO2(g) + 4H2O(g)
660. g CO2
360. g H2O
The amount of product, for a given amount of reactant, is calculated based on their molar/stoichiometric ratio. So, the first step is to determine the moles of propane. The overall plan is:
The moles of C3H8 are calculated using its molar mass:
\[{\rm{n(}}{{\rm{C}}_{\rm{3}}}{{\rm{H}}_{\rm{8}}}{\rm{)}}\;{\rm{ = }}\;{\rm{220}}{\rm{.5}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{44}}{\rm{.1}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{5}}{\rm{.00}}\;{\rm{mol}}\]
Next, we find the moles of CO2 based on its molar ratio with C3H8:
\[{\rm{n}}\left( {{\rm{C}}{{\rm{O}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{5}}{\rm{.00 }}\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{3}}}{{\rm{H}}_{\rm{8}}}}}\;{\rm{ \times }}\;\frac{{{\rm{3}}\;{\rm{mol}}\;{\rm{C}}{{\rm{O}}_{\rm{2}}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{3}}}{{\rm{H}}_{\rm{8}}}}}}}\;{\rm{ = }}\;{\rm{15}}{\rm{.0}}\;{\rm{mol}}\]
And finally, the mass of the CO2 is determined using its moles and molar mass:
\[{\rm{m}}\left( {{\rm{C}}{{\rm{O}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{15}}{\rm{.0 }}\cancel{{{\rm{mol}}\;}}\;{\rm{ \times }}\;\frac{{{\rm{44}}{\rm{.0}}\;{\rm{g}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;}}}}\;{\rm{ = }}\;{\rm{660}}{\rm{.}}\;{\rm{g}}\]
Follow the same procedure to find the mass of H2O:
\[{\rm{n}}\left( {{{\rm{H}}_{\rm{2}}}{\rm{O}}} \right)\;{\rm{ = }}\;{\rm{5}}{\rm{.00 }}\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{3}}}{{\rm{H}}_{\rm{8}}}}}\;{\rm{ \times }}\;\frac{{{\rm{4}}\;{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}{\rm{O}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{3}}}{{\rm{H}}_{\rm{8}}}}}}}\;{\rm{ = }}\;{\rm{20}}{\rm{.0}}\;{\rm{mol}}\]
\[{\rm{m}}\left( {{{\rm{H}}_{\rm{2}}}{\rm{O}}} \right)\;{\rm{ = }}\;{\rm{20}}{\rm{.0 }}\cancel{{{\rm{mol}}\;}}\;{\rm{ \times }}\;\frac{{{\rm{18}}{\rm{.0}}\;{\rm{g}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;}}}}\;{\rm{ = }}\;{\rm{360}}{\rm{.}}\;{\rm{g}}\]
How many grams of CaCl2 can be produced from 65.0 g of Ca(OH)2 according to the following reaction,
Ca(OH)2 + 2HCl → CaCl2 + 2H2O
97.3 g
Here is the conceptual plan for solving this problem:
The moles of Ca(OH)2 are calculated using its molar mass:
\[{\rm{n}}\;{\rm{(Ca}}{\left( {{\rm{OH}}} \right)_{\rm{2}}}{\rm{)}}\;{\rm{ = }}\;{\rm{65}}{\rm{.0}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{74}}{\rm{.1}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.877}}\;{\rm{mol}}\]
Next, we find the moles of CaCl2 based on its molar ratio with Ca(OH)2:
\[{\rm{n}}\;\left( {{\rm{CaC}}{{\rm{l}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.877 }}\cancel{{{\rm{mol}}\;{\rm{Ca}}{{\left( {{\rm{OH}}} \right)}_{\rm{2}}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}\;{\rm{CaC}}{{\rm{l}}_{\rm{2}}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{Ca}}{{\left( {{\rm{OH}}} \right)}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.877}}\;{\rm{mol}}\]
Notice that moles of CaCl2 are equal to the moles of Ca(OH)2. This is because of their 1:1 molar ratio in the equation.
The last step is converting the moles to mass of the CaCl2:
\[{\rm{m}}\left( {{\rm{CaC}}{{\rm{l}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.877 }}\cancel{{{\rm{mol}}\;}}\;{\rm{ \times }}\;\frac{{{\rm{111}}\;{\rm{g}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;}}}}\;{\rm{ = }}\;{\rm{97}}{\rm{.3}}\;{\rm{g}}\]
This process can, and often is shown as a one-step conversion as we do in dimensional analysis. It would be as follows:
\[{\rm{m}}\left( {{\rm{CaC}}{{\rm{l}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{65}}{\rm{.0}}\;{\cancel{{{\rm{g}}\;{\rm{Ca}}{{\left( {{\rm{OH}}} \right)}_{\rm{2}}}}}_{\rm{\;}}}{\rm{ \times }}\;\frac{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{Ca}}{{\left( {{\rm{OH}}} \right)}_{\rm{2}}}}}}}{{{\rm{74}}{\rm{.1}}\;\cancel{{{\rm{g}}\;{\rm{Ca}}{{\left( {{\rm{OH}}} \right)}_{\rm{2}}}}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{CaC}}{{\rm{l}}_{\rm{2}}}}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{Ca}}{{\left( {{\rm{OH}}} \right)}_{\rm{2}}}}}}}\; \times \;\frac{{{\rm{111}}\;{\rm{g}}\;{\rm{CaC}}{{\rm{l}}_{\rm{2}}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{CaC}}{{\rm{l}}_{\rm{2}}}\;}}}}\;\;{\rm{ = }}\;{\rm{97}}{\rm{.3}}\;{\rm{g}}\]
This method is completely fine, however, I prefer doing these conversions stepwise to better see what happens in each step, and therefore, most exercises will be solved by doing one conversion at a time.
How many moles of oxygen are formed when 75.0 g of Cu(NO3)2 decomposes according to the following reaction?
2Cu(NO3)2 → 2CuO + 4NO2 + O2
0.200 mol
The amount of product, for a given amount of reactant, is calculated based on their molar/stoichiometric ratio.
So, the conceptual plan is:
\[{\rm{n}}\;{\rm{(Cu}}{\left( {{\rm{N}}{{\rm{O}}_{\rm{3}}}} \right)_{\rm{2}}}{\rm{\;)}}\;{\rm{ = }}\;{\rm{75}}{\rm{.0}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{187}}{\rm{.5}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.400}}\;{\rm{mol}}\]
\[{\rm{n}}\;\left( {{{\rm{O}}_{{\rm{2\;}}}}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.400}}\;\cancel{{{\rm{mol}}\;{\rm{Cu}}{{\left( {{\rm{N}}{{\rm{O}}_{\rm{3}}}} \right)}_{\rm{2}}}{\rm{\;}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}\;{{\rm{O}}_{\rm{2}}}}}{{\cancel{{{\rm{2}}\;{\rm{mol}}\;{\rm{Cu}}{{\left( {{\rm{N}}{{\rm{O}}_{\rm{3}}}} \right)}_{\rm{2}}}{\rm{\;}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.200}}\;{\rm{mol}}\]
How many grams of MnCl2 can be prepared from 52.1 grams of MnO2?
MnO2 + 4HCl → MnCl2 + Cl2 + 2H2O
75.5 g
The amount of product, for a given amount of reactant, is calculated based on their molar/stoichiometric ratio. So, the first step is to determine the moles of propane. The overall plan is:
The moles of MnO2 are calculated using its molar mass:
\[{\rm{n}}\;{\rm{(Mn}}{{\rm{O}}_{\rm{2}}}{\rm{)}}\;{\rm{ = }}\;{\rm{52}}{\rm{.1}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{86}}{\rm{.9}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.600}}\;{\rm{mol}}\]
Next, we find the moles of MnCl2 based on its molar ratio with MnO2:
\[{\rm{n}}\;\left( {{\rm{MnC}}{{\rm{l}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.600 }}\cancel{{{\rm{mol}}\;{\rm{Mn}}{{\rm{O}}_{\rm{2}}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}\;{\rm{MnC}}{{\rm{l}}_{\rm{2}}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{Mn}}{{\rm{O}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.600}}\;{\rm{mol}}\]
And finally, the mass of the MnCl2 is determined using its moles and molar mass:
\[{\rm{m}}\left( {{\rm{MnC}}{{\rm{l}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.600 }}\cancel{{{\rm{mol}}\;}}\;{\rm{ \times }}\;\frac{{{\rm{125}}{\rm{.8}}\;{\rm{g}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;}}}}\;{\rm{ = }}\;{\rm{75}}{\rm{.5g}}\]
Determine the mass of oxygen that is formed when an 18.3-g sample of potassium chlorate is decomposed according to the following equation:
2KClO3(s) → 2KCl(s) + 3O2(g).
7.16 g
The amount of product, for a given amount of reactant, is calculated based on their molar/stoichiometric ratio. So, the first step is to determine the moles of propane. The conceptual plan is:
The moles of MnO2 are calculated using its molar mass:
\[{\rm{n}}\;{\rm{(KCl}}{{\rm{O}}_{\rm{3}}}{\rm{)}}\;{\rm{ = }}\;{\rm{18}}{\rm{.3}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{122}}{\rm{.6}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.149}}\;{\rm{mol}}\]
Next, we find the moles of O2 based on its molar ratio with KClO3:
\[{\rm{n}}\;\left( {{{\rm{O}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.149 }}\cancel{{{\rm{mol}}\;{\rm{KCl}}{{\rm{O}}_{\rm{3}}}}}\;{\rm{ \times }}\;\frac{{{\rm{3}}\;{\rm{mol}}\;{{\rm{O}}_{\rm{2}}}}}{{{\rm{2}}\;\cancel{{{\rm{mol}}\;{\rm{KCl}}{{\rm{O}}_{\rm{3}}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.224}}\;{\rm{mol}}\]
And finally, the mass of the MnCl2 is determined using its moles and molar mass:
\[{\rm{m}}\left( {{{\rm{O}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.224 }}\cancel{{{\rm{mol}}\;}}\;{\rm{ \times }}\;\frac{{{\rm{32}}{\rm{.0}}\;{\rm{g}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;}}}}\;{\rm{ = }}\;{\rm{7}}{\rm{.16}}\;{\rm{g}}\]
How many grams of H2O will be formed when 48.0 grams H2 are mixed with excess hydrogen gas?
2H2 + O2 → 2H2O
432 g
The amount of product, for a given amount of reactant, is calculated based on their molar/stoichiometric ratio. So, the first step is to determine the moles of propane. The conceptual plan is:
The moles of H2O are calculated using its molar mass:
\[{\rm{n}}\;{\rm{(}}{{\rm{H}}_2}{\rm{)}}\;{\rm{ = }}\;{\rm{48}}{\rm{.0}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{2}}{\rm{.00}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{24}}{\rm{.0}}\;{\rm{mol}}\]
Next, we find the moles of H2O based on its molar ratio with H2:
\[{\rm{n}}\;\left( {{{\rm{H}}_{\rm{2}}}{\rm{O}}} \right)\;{\rm{ = }}\;{\rm{24}}{\rm{.0 }}\cancel{{{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}}}\;{\rm{ \times }}\;\frac{{{\rm{2}}\;{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}{\rm{O}}}}{{{\rm{2}}\;\cancel{{{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{24}}{\rm{.0}}\;{\rm{mol}}\]
And finally, the mass of the H2O is determined using its moles and molar mass:
\[{\rm{m}}\left( {{{\rm{H}}_{\rm{2}}}{\rm{O}}} \right)\;{\rm{ = }}\;{\rm{24}}{\rm{.0 }}\cancel{{{\rm{mol}}\;}}\;{\rm{ \times }}\;\frac{{{\rm{18}}{\rm{.0}}\;{\rm{g}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;}}}}\;{\rm{ = }}\;{\rm{432}}\;{\rm{g}}\]
Consider the chlorination reaction of methane (CH4):
CH4(g) + 4Cl2(g) → CCl4(g) + 4HCl(g)
How many moles of CH4 were used in the reaction if 51.9 g of CCl4 were obtained?
0.337 mol
The amount of a reactant, for a given amount of product, is calculated based on their molar/stoichiometric ratio. So, the first step is to determine the moles of carbon tetrachloride, CCl4. The conceptual plan is:
The moles of CCl4 are calculated using its molar mass:
\[{\rm{n}}\;{\rm{(CC}}{{\rm{l}}_{\rm{4}}}{\rm{)}}\;{\rm{ = }}\;{\rm{51}}{\rm{.9}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{153}}{\rm{.8}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.337}}\;{\rm{mol}}\]
Next, we find the moles of CH4 based on its molar ratio with CCl4. It is a 1:1 ratio, so there is going to be 0.337 mol CH4:
\[{\rm{n}}\;\left( {{\rm{C}}{{\rm{H}}_{\rm{4}}}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.337 }}\cancel{{{\rm{mol}}\;{\rm{CC}}{{\rm{l}}_{\rm{4}}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}\;{\rm{C}}{{\rm{H}}_{\rm{4}}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{CC}}{{\rm{l}}_{\rm{4}}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.337}}\;{\rm{mol}}\]
How many grams of Ba(NO3)2 can be produced by reacting 16.5 g of HNO3 with an excess of Ba(OH)2?
34.2 g
We need to first write the balanced chemical equation to do the calculations:
Ba(OH)2 + 2HNO3 → Ba(NO3)2 + 2H2O
The conceptual plan would be:
So, let’s start with the moles of HNO3:
\[{\rm{n}}\;{\rm{(HN}}{{\rm{O}}_{\rm{3}}}{\rm{)}}\;{\rm{ = }}\;{\rm{16}}{\rm{.5}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{63}}{\rm{.0}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.262}}\;{\rm{mol}}\]
Once we have the moles, we can determine the moles of Ba(NO3)2 based on the molar ratio, and then convert the moles to the mass:
\[{\rm{n}}\;\left( {{\rm{Ba}}{{\left( {{\rm{N}}{{\rm{O}}_{\rm{3}}}} \right)}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.262 }}\cancel{{{\rm{mol}}\;{\rm{HN}}{{\rm{O}}_{\rm{3}}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}\;{\rm{Ba}}{{\left( {{\rm{N}}{{\rm{O}}_{\rm{3}}}} \right)}_{\rm{2}}}}}{{{\rm{2}}\;\cancel{{{\rm{mol}}\;{\rm{HN}}{{\rm{O}}_{\rm{3}}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.131}}\;{\rm{mol}}\]
\[{\rm{m}}\left( {{\rm{Ba}}{{\left( {{\rm{N}}{{\rm{O}}_{\rm{3}}}} \right)}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.131 }}\cancel{{{\rm{mol}}\;}}\;{\rm{ \times }}\;\frac{{{\rm{261}}{\rm{.3}}\;{\rm{g}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;}}}}\;{\rm{ = }}\;{\rm{34}}{\rm{.2}}\;{\rm{g}}\]
Ethanol can be obtained by fermentation – a complex chemical process breaking down glucose to ethanol and carbon dioxide.
C6H12O6 → 2C2H5OH + 2CO2
glucose ethanol
How many mL of ethanol (d =0.789 g/mL) can be obtained by this process starting with 286 g of glucose?
186 mL
This problem has an additional step of converting the mass of the product to volume. Other than that, we follow the same strategy and steps as in the previous problems:
\[{\rm{n}}\;{\rm{(}}{{\rm{C}}_{\rm{6}}}{{\rm{H}}_{{\rm{12}}}}{{\rm{O}}_{\rm{6}}}{\rm{)}}\;{\rm{ = }}\;{\rm{286}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{180}}{\rm{.2}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{1}}{\rm{.59}}\;{\rm{mol}}\]
Now, we can find the moles of C2H5OH:
\[{\rm{n}}\;\left( {{{\rm{C}}_{\rm{2}}}{{\rm{H}}_{\rm{5}}}{\rm{OH}}} \right)\;{\rm{ = }}\;{\rm{1}}{\rm{.59 }}\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{6}}}{{\rm{H}}_{{\rm{12}}}}{{\rm{O}}_{\rm{6}}}}}\;{\rm{ \times }}\;\frac{{{\rm{2}}\;{\rm{mol}}\;{{\rm{C}}_{\rm{2}}}{{\rm{H}}_{\rm{5}}}{\rm{OH}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{6}}}{{\rm{H}}_{{\rm{12}}}}{{\rm{O}}_{\rm{6}}}}}}}\;{\rm{ = }}\;{\rm{3}}{\rm{.18}}\;{\rm{mol}}\]
\[{\rm{m}}\left( {{{\rm{C}}_{\rm{2}}}{{\rm{H}}_{\rm{5}}}{\rm{OH}}} \right)\;{\rm{ = }}\;{\rm{3}}{\rm{.18 }}\cancel{{{\rm{mol}}\;}}\;{\rm{ \times }}\;\frac{{{\rm{46}}{\rm{.1}}\;{\rm{g}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;}}}}\;{\rm{ = }}\;{\rm{147}}\;{\rm{g}}\]
The last step is converting the mass to volume:
\[{\rm{v}}\left( {{{\rm{C}}_{\rm{2}}}{{\rm{H}}_{\rm{5}}}{\rm{OH}}} \right)\;{\rm{ = }}\;{\rm{147}}\;\cancel{{\rm{g}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mL}}}}{{{\rm{0}}{\rm{.789}}\;\cancel{{\rm{g}}}}}\;{\rm{ = }}\;{\rm{186}}\;{\rm{mL}}\]
36.0 g of butane (C4H10) was burned in an excess of oxygen and the resulting carbon dioxide (CO2) was collected in a sealed vessel.
2C4H10 + 13O2 → 8CO2 + 10H2O
How many grams of LiOH will be necessary to consume all the CO2 from the first reaction?
2LiOH + CO2 → Li2CO3 + H2O
119 g
There are two reactions here, and the link between them is the CO2 that is formed in the first reaction and used in the second.
So, the plan would be to determine the moles of CO2 in the first reaction, and use it to calculate the moles, and consequently the mass of LiOH.
\[{\rm{n}}\;{\rm{(}}{{\rm{C}}_{\rm{4}}}{{\rm{H}}_{{\rm{10}}}}{\rm{)}}\;{\rm{ = }}\;{\rm{36}}{\rm{.0}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{58}}{\rm{.1}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.620}}\;{\rm{mol}}\]
\[{\rm{n}}\;\left( {{\rm{C}}{{\rm{O}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.620 }}\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{4}}}{{\rm{H}}_{{\rm{10}}}}}}\;{\rm{ \times }}\;\frac{{{\rm{8}}\;{\rm{mol}}\;{\rm{C}}{{\rm{O}}_{\rm{2}}}}}{{{\rm{2}}\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{4}}}{{\rm{H}}_{{\rm{10}}}}}}}}\;{\rm{ = }}\;{\rm{2}}{\rm{.48}}\;{\rm{mol}}\]
This is the amount of CO2 that will be reacted with LiOH in a 1:2 ratio. So, we can determine the moles of LiOH and convert them to the mass:
\[{\rm{n}}\;\left( {{\rm{LiOH}}} \right)\;{\rm{ = }}\;{\rm{2}}{\rm{.48 }}\cancel{{{\rm{mol}}\;{\rm{C}}{{\rm{O}}_{\rm{2}}}}}\;{\rm{ \times }}\;\frac{{{\rm{2}}\;{\rm{mol}}\;{\rm{LiOH}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{C}}{{\rm{O}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{4}}{\rm{.96}}\;{\rm{mol}}\]
\[{\rm{m}}\;\left( {{\rm{LiOH}}} \right)\;{\rm{ = }}\;{\rm{4}}{\rm{.96}}\;\cancel{{{\rm{mol}}\;{\rm{LiOH}}}}\;{\rm{ \times }}\;\frac{{{\rm{24}}{\rm{.0}}\;{\rm{g}}\;{\rm{LiOH}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{LiOH}}}}}}\;{\rm{ = }}\;{\rm{119}}\;{\rm{g}}\;\]
Limiting Reactant
13. Which statement about limiting reactant is correct?
a) The limiting reactant is the one in a smaller quantity.
b) The limiting reactant is the one in greater quantity.
c) The limiting reactant is the one producing less product.
d) The limiting reactant is the one producing more product.
c) The limiting reactant is the one producing less product than any of the other reactants.
Find the limiting reactant for each initial amount of reactants.
4NH3 + 5O2 → 4NO + 6H2O
a) 2 mol of NH3 and 2 mol of O2
b) 2 mol of NH3 and 3 mol of O2
c) 3 mol of NH3 and 3 mol of O2
d) 3 mol of NH3 and 2 mol of O2
Note: This is not a multiple-choice question. Each row represents a separate question where you need to determine the limiting reactant.
a) 2 mol of NH3 and 2 mol of O2
b) 2 mol of NH3 and 3 mol of O2
c) 3 mol of NH3 and 3 mol of O2
d) 3 mol of NH3 and 2 mol of O2
The limiting reactant is the one producing less product. So, to determine the limiting reactant for each pair, we need to pick a product (NO or H2O) and see whether NH3 or O2 will produce less product for the given mole ratio.
Let’s do the calculations based on the amount of NO that can be formed.
a)
\[{\rm{n}}\;\left( {{\rm{NO}}} \right)\;{\rm{ = }}\;{\rm{2 }}\cancel{{{\rm{mol}}\;{\rm{N}}{{\rm{H}}_{\rm{3}}}}}\;{\rm{ \times }}\;\frac{{{\rm{4}}\;{\rm{mol}}\;{\rm{NO}}}}{{{\rm{4}}\;\cancel{{{\rm{mol}}\;{\rm{N}}{{\rm{H}}_{\rm{3}}}}}}}\;{\rm{ = }}\;{\rm{2}}\;{\rm{mol}}\]
\[{\rm{n}}\;\left( {{\rm{NO}}} \right)\;{\rm{ = }}\;{\rm{2 }}\cancel{{{\rm{mol}}\;{{\rm{O}}_2}}}\;{\rm{ \times }}\;\frac{{{\rm{4}}\;{\rm{mol}}\;{\rm{NO}}}}{{{\rm{5}}\;\cancel{{{\rm{mol}}\;{{\rm{O}}_2}}}}}\;{\rm{ = }}\;{\rm{1}}{\rm{.6}}\;{\rm{mol}}\]
So, for (a), O2 is the limiting reactant.
b)
\[{\rm{n}}\;\left( {{\rm{NO}}} \right)\;{\rm{ = }}\;{\rm{2 }}\cancel{{{\rm{mol}}\;{\rm{N}}{{\rm{H}}_{\rm{3}}}}}\;{\rm{ \times }}\;\frac{{{\rm{4}}\;{\rm{mol}}\;{\rm{NO}}}}{{{\rm{4}}\;\cancel{{{\rm{mol}}\;{\rm{N}}{{\rm{H}}_{\rm{3}}}}}}}\;{\rm{ = }}\;{\rm{2}}\;{\rm{mol}}\]
\[{\rm{n}}\;\left( {{\rm{NO}}} \right)\;{\rm{ = }}\;{\rm{3 }}\cancel{{{\rm{mol}}\;{{\rm{O}}_2}}}\;{\rm{ \times }}\;\frac{{{\rm{4}}\;{\rm{mol}}\;{\rm{NO}}}}{{{\rm{5}}\;\cancel{{{\rm{mol}}\;{{\rm{O}}_2}}}}}\;{\rm{ = }}\;{\rm{2}}{\rm{.4}}\;{\rm{mol}}\]
So, for (b), NO is the limiting reactant.
c)
\[{\rm{n}}\;\left( {{\rm{NO}}} \right)\;{\rm{ = }}\;{\rm{3 }}\cancel{{{\rm{mol}}\;{\rm{N}}{{\rm{H}}_{\rm{3}}}}}\;{\rm{ \times }}\;\frac{{{\rm{4}}\;{\rm{mol}}\;{\rm{NO}}}}{{{\rm{4}}\;\cancel{{{\rm{mol}}\;{\rm{N}}{{\rm{H}}_{\rm{3}}}}}}}\;{\rm{ = }}\;{\rm{3}}\;{\rm{mol}}\]
\[{\rm{n}}\;\left( {{\rm{NO}}} \right)\;{\rm{ = }}\;{\rm{3 }}\cancel{{{\rm{mol}}\;{{\rm{O}}_2}}}\;{\rm{ \times }}\;\frac{{{\rm{4}}\;{\rm{mol}}\;{\rm{NO}}}}{{{\rm{5}}\;\cancel{{{\rm{mol}}\;{{\rm{O}}_2}}}}}\;{\rm{ = }}\;{\rm{2}}{\rm{.4}}\;{\rm{mol}}\]
So, for (c), O2 is the limiting reactant.
d)
\[{\rm{n}}\;\left( {{\rm{NO}}} \right)\;{\rm{ = }}\;{\rm{3 }}\cancel{{{\rm{mol}}\;{\rm{N}}{{\rm{H}}_{\rm{3}}}}}\;{\rm{ \times }}\;\frac{{{\rm{4}}\;{\rm{mol}}\;{\rm{NO}}}}{{{\rm{4}}\;\cancel{{{\rm{mol}}\;{\rm{N}}{{\rm{H}}_{\rm{3}}}}}}}\;{\rm{ = }}\;{\rm{3}}\;{\rm{mol}}\]
\[{\rm{n}}\;\left( {{\rm{NO}}} \right)\;{\rm{ = }}\;{\rm{2 }}\cancel{{{\rm{mol}}\;{{\rm{O}}_2}}}\;{\rm{ \times }}\;\frac{{{\rm{4}}\;{\rm{mol}}\;{\rm{NO}}}}{{{\rm{5}}\;\cancel{{{\rm{mol}}\;{{\rm{O}}_2}}}}}\;{\rm{ = }}\;{\rm{1}}{\rm{.6}}\;{\rm{mol}}\]
So, for (d), O2 is the limiting reactant.
The shorter way of determining the limiting reactant is to divide the moles of a given reactant by its coefficient in the chemical reaction. This is the effective quantity of the reactant as it takes into consideration not only the amount of the reactant but also its molar ratio in the reaction.
Let’s put the equation and the moles here and determine the LR by the ratio of the moles and coefficient:
4NH3 + 5O2 → 4NO + 6H2O
a) 2 mol of NH3 and 2 mol of O2
b) 2 mol of NH3 and 3 mol of O2
c) 3 mol of NH3 and 3 mol of O2
d) 3 mol of NH3 and 2 mol of O2
So, for (a), we are comparing 2/4 mol of NH3 with 2/5 mol of O2, and therefore, O2 is the LR.
For (b), we are comparing 2/4 mol of NH3 with 3/5 mol of O2, and therefore, NH3 is the LR.
For (c), we are comparing 3/4 mol of NH3 with 3/5 mol of O2, and therefore, O2 is the LR.
For (d), 3 mol of NH3 and 3/4 mol of NH3 with 2/5 mol of O2, and therefore, O2 is the LR.
How many g of hydrogen are left over in producing ammonia when 14.0 g of nitrogen is reacted with 8.0 g of hydrogen?
N2(g) + 3 H2(g) → 2 NH3(g)
5.0 g
When the amounts of both reactants are given, you must determine the LR and then, based on the moles of the LR, determine the amount of product(s) that can be formed. This is the standard procedure when working on examples covering limiting reactant.
Now, in this problem, we are not asked to determine the amount of any product, but rather we need to determine how much hydrogen is left out once the reaction is complete. This already tells us that the nitrogen is the LR because some of the hydrogen remains unreacted, so it must’ve been in excess.
The first step is, as always, to determine the moles of the reactants, then using the mole ratio, calculate how much hydrogen has reacted. The remaining mass of the hydrogen is calculated by subtracting this amount from the initial mass.
\[{\rm{n}}\;{\rm{(}}{{\rm{N}}_{\rm{2}}}{\rm{)}}\;{\rm{ = }}\;{\rm{14}}{\rm{.0}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{28}}{\rm{.0}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.500}}\;{\rm{mol}}\]
\[{\rm{n}}\;{\rm{(}}{{\rm{H}}_{\rm{2}}}{\rm{)}}\;{\rm{ = }}\;{\rm{8}}{\rm{.0}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{2}}{\rm{.0}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{4}}{\rm{.0}}\;{\rm{mol}}\]
The moles of hydrogen reacted are calculated based on the moles of the nitrogen which is the limiting reactant:
\[{\rm{n}}\;\left( {{{\rm{H}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.500 }}\cancel{{{\rm{mol}}\;{{\rm{N}}_2}}}\;{\rm{ \times }}\;\frac{{{\rm{3}}\;{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{{\rm{N}}_2}}}}}\;{\rm{ = }}\;{\rm{1}}{\rm{.50}}\;{\rm{mol}}\]
So, there are:
4.0 – 1.50 = 2.5 mol H2 left out
\[{\rm{m}}\;{\rm{(}}{{\rm{H}}_{\rm{2}}}{\rm{)}}\;{\rm{ = }}\;{\rm{2}}{\rm{.5}}\;{\rm{mol}}\;{\rm{ \times }}\;\frac{{{\rm{2}}{\rm{.0}}\;{\rm{g}}}}{{{\rm{1}}\;{\rm{mol}}}}\;{\rm{ = }}\;{\rm{5}}{\rm{.0}}\;{\rm{g}}\]
How many grams of PCl3 will be produced if 130.5 g Cl2 is reacted with 56.4 g P4 according to the following equation?
6Cl2(g) + P4(s) → 4PCl3(l)
169 g
When the amounts of both reactants are given, you must determine the LR and then, based on the moles of the LR, determine the amount of product(s) that can be formed.
The moles of Cl2 and P4 are:
\[{\rm{n}}\;{\rm{(C}}{{\rm{l}}_{\rm{2}}}{\rm{)}}\;{\rm{ = }}\;130.5\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{70}}{\rm{.9}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{1}}{\rm{.84}}\;{\rm{mol}}\]
\[{\rm{n}}\;{\rm{(}}{{\rm{P}}_{\rm{4}}}{\rm{)}}\;{\rm{ = }}\;{\rm{56}}{\rm{.4}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{123}}{\rm{.9}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.455}}\;{\rm{mol}}\]
Next, we calculate how much PCl3 can be formed from each reactant:
\[{\rm{n}}\;\left( {{\rm{PC}}{{\rm{l}}_{\rm{3}}}} \right)\;{\rm{ = }}\;{\rm{1}}{\rm{.84 }}\cancel{{{\rm{mol}}\;{\rm{C}}{{\rm{l}}_{\rm{2}}}}}\;{\rm{ \times }}\;\frac{{{\rm{4}}\;{\rm{mol}}\;{\rm{PC}}{{\rm{l}}_{\rm{3}}}}}{{{\rm{6}}\;\cancel{{{\rm{mol}}\;{\rm{C}}{{\rm{l}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{1}}{\rm{.23}}\;{\rm{mol}}\]
\[{\rm{n}}\;\left( {{\rm{PC}}{{\rm{l}}_{\rm{3}}}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.455 }}\cancel{{{\rm{mol}}\;{{\rm{P}}_{\rm{4}}}}}\;{\rm{ \times }}\;\frac{{{\rm{4}}\;{\rm{mol}}\;{\rm{PC}}{{\rm{l}}_{\rm{3}}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{{\rm{P}}_{\rm{4}}}}}}}\;{\rm{ = }}\;{\rm{1}}{\rm{.82}}\;{\rm{mol}}\]
Cl2 gives less PCl3 and therefore, it is the LR and 1.23 mol of PCl3 can be produced in this reaction.
The mass of PCl3 is:
\[{\rm{m}}\;{\rm{(PC}}{{\rm{l}}_{\rm{3}}}{\rm{)}}\;{\rm{ = }}\;{\rm{1}}{\rm{.23}}\;{\rm{mol}}\;{\rm{ \times }}\;\frac{{{\rm{137}}{\rm{.3}}\;{\rm{g}}}}{{{\rm{1}}\;{\rm{mol}}}}\;{\rm{ = }}\;{\rm{169}}\;{\rm{g}}\]
How many grams of sulfur can be obtained if 12.6 g H2S is reacted with 14.6 g SO2 according to the following equation?
2H2S(g) + SO2(g) → 3S(s) + 2H2O(g)
17.8 g
When the amount of both reactants is given, you must determine the LR and then, based on the moles of the LR, determine the amount of product(s) that can be formed.
The moles of H2S and SO2 are:
\[{\rm{n}}\;{\rm{(}}{{\rm{H}}_{\rm{2}}}{\rm{S)}}\;{\rm{ = }}\;{\rm{12}}{\rm{.6}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{34}}{\rm{.1}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.370}}\;{\rm{mol}}\]
\[{\rm{n}}\;{\rm{(S}}{{\rm{O}}_{\rm{2}}}{\rm{)}}\;{\rm{ = }}\;{\rm{14}}{\rm{.6}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{64}}{\rm{.1}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.228}}\;{\rm{mol}}\]
Next, we calculate how much PCl3 can be formed from each reactant:
\[{\rm{n}}\;\left( {\rm{S}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.370 }}\cancel{{{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}{\rm{S}}}}\;{\rm{ \times }}\;\frac{{{\rm{3}}\;{\rm{mol}}\;{\rm{S}}}}{{{\rm{2}}\;\cancel{{{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}{\rm{S}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.555}}\;{\rm{mol}}\]
\[{\rm{n}}\;\left( {\rm{S}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.228 }}\cancel{{{\rm{mol}}\;{\rm{S}}{{\rm{O}}_{\rm{2}}}}}\;{\rm{ \times }}\;\frac{{{\rm{3}}\;{\rm{mol}}\;{\rm{S}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{S}}{{\rm{O}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.684}}\;{\rm{mol}}\]
H2S gives less S and therefore, it is the LR and 0.555 mol of S can be produced in this reaction.
The mass of S is:
\[{\rm{m}}\;{\rm{(S)}}\;{\rm{ = }}\;{\rm{0}}{\rm{.555}}\;{\rm{mol}}\;{\rm{ \times }}\;\frac{{{\rm{32}}{\rm{.1}}\;{\rm{g}}}}{{{\rm{1}}\;{\rm{mol}}}}\;{\rm{ = }}\;{\rm{17}}{\rm{.8}}\;{\rm{g}}\]
The following equation represents the combustion of octane, C8H18, a component of gasoline:
2C8H18(g) + 25O2(g) → 16CO2(g) + 18H2O(g)
Will 356 g of oxygen be enough for the complete combustion of 954 g of octane?
356 g of oxygen is not enough for the complete combustion of 954 g of octane.
First, calculate the moles of the reactants:
\[{\rm{n}}\;{\rm{(}}{{\rm{O}}_{\rm{2}}}{\rm{)}}\;{\rm{ = }}\;{\rm{356}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{32}}{\rm{.0}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{11}}{\rm{.4}}\;{\rm{mol}}\]
\[{\rm{n}}\;{\rm{(}}{{\rm{C}}_{\rm{8}}}{{\rm{H}}_{{\rm{18}}}}{\rm{)}}\;{\rm{ = }}\;{\rm{954}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{114}}{\rm{.2}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{8}}{\rm{.35}}\;{\rm{mol}}\]
And now let’s see how many moles of O2 are needed to react with 8.35 mol of C8H18:
\[{\rm{n}}\;\left( {{{\rm{O}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{8}}{\rm{.35 }}\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{8}}}{{\rm{H}}_{{\rm{18}}}}}}\;{\rm{ \times }}\;\frac{{{\rm{25}}\;{\rm{mol}}\;{{\rm{O}}_{\rm{2}}}}}{{{\rm{2}}\;\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{8}}}{{\rm{H}}_{{\rm{18}}}}}}}}\;{\rm{ = }}\;{\rm{104}}\;{\rm{mol}}\]
104 moles of O2 are needed to react with only 8.35 mol of C8H18 and this is because of the 25:2 mole ratio. So, 356 g of oxygen is not enough for the complete combustion of 954 g of octane.
When 140.0 g of AgNO3 was added to an aqueous solution of NaCl, 86.0 g of AgCl was collected as a white precipitate. Which salt was the limiting reactant in this reaction? How many grams of NaCl were present in the solution when AgNO3 was added?
AgNO3(aq) + NaCl(aq) → AgCl(s) + NaNO3(aq)
NaCl was the limiting reactant and 35.0 g of it were present in the solution when AgNO3 was added.
We need to find the moles of AgCl which will allow us to calculate how much AgNO3 and NaCl had reacted in the reaction.
\[{\rm{n}}\;{\rm{(AgCl)}}\;{\rm{ = }}\;{\rm{86}}{\rm{.0}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{143}}{\rm{.3}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.600}}\;{\rm{mol}}\]
The stoichiometric ratio of all the reactants and products is1:1, and therefore, there were 0.600 mol of AgNO3 and 0.600 mol of NaCl participating in the reaction.
Now, let’s calculate the moles of 140.0 g of AgNO3 and see whether it corresponds to 0.600 mol. If it is more than that, then AgNO3 was added in excess and NaCl must be the limiting reactant:
\[{\rm{n}}\;{\rm{(AgN}}{{\rm{O}}_{\rm{3}}}{\rm{)}}\;{\rm{ = }}\;{\rm{140}}{\rm{.0}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{169}}{\rm{.9}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.824}}\;{\rm{mol}}\]
So, 0.824 mol of AgNO3 were added to the solution, but only 0.600 mol had reacted which means that is how much NaCl was present in the solution, and it was not enough to react with all the AgNO3.
And this confirms that AgNO3 was added in excess and NaCl is the limiting reactant.
In the last step, we determine the mass of 0.600 mol NaCl that was in the solution when AgNO3 was added:
\[{\rm{m}}\;{\rm{(NaCl)}}\;{\rm{ = }}\;{\rm{0}}{\rm{.600}}\;{\rm{mol}}\;{\rm{ \times }}\;\frac{{{\rm{58}}{\rm{.4}}\;{\rm{g}}}}{{{\rm{1}}\;{\rm{mol}}}}\;{\rm{ = }}\;{\rm{35}}{\rm{.0}}\;{\rm{g}}\]
Consider the reaction between MnO2 and HCl:
MnO2 + 4HCl → MnCl2 + Cl2 + 2H2O
What is the theoretical yield of MnCl2 in grams when 165 g of MnO2 is added to a solution containing 94.2 g of HCl?
0.645 mol or 81.1 g MnCl2
The theoretical yield is the amount of product that can be formed, so this problem is similar to the ones we have been working on.
The amounts of both reactants are given, so we determine the LR and then, based on the moles of the LR, determine the amount of product(s) that can be formed.
The moles of MnO2 and HCl are:
\[{\rm{n}}\;{\rm{(Mn}}{{\rm{O}}_{\rm{2}}}{\rm{)}}\;{\rm{ = }}\;{\rm{165}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{86}}{\rm{.9}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{1}}{\rm{.90}}\;{\rm{mol}}\]
\[{\rm{n}}\;{\rm{(HCl)}}\;{\rm{ = }}\;{\rm{94}}{\rm{.2}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{36}}{\rm{.5}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{2}}{\rm{.58}}\;{\rm{mol}}\]
Next, we calculate how much MnCl2 can be formed from each reactant:
\[{\rm{n}}\;\left( {{\rm{MnC}}{{\rm{l}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{1}}{\rm{.90 }}\cancel{{{\rm{mol}}\;{\rm{Mn}}{{\rm{O}}_{\rm{2}}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}\;{\rm{MnC}}{{\rm{l}}_{\rm{2}}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{Mn}}{{\rm{O}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{1}}{\rm{.90}}\;{\rm{mol}}\]
\[{\rm{n}}\;\left( {{\rm{MnC}}{{\rm{l}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{2}}{\rm{.58 }}\cancel{{{\rm{mol}}\;{\rm{HCl}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}\;{\rm{MnC}}{{\rm{l}}_{\rm{2}}}}}{{{\rm{4}}\;\cancel{{{\rm{mol}}\;{\rm{HCl}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.645}}\;{\rm{mol}}\]
HCl gives less product so, it is the LR, and therefore, 0.645 mol MnCl2 is the theoretical yield of the reaction.
If you are asked to find the theoretical yield in grams, then convert the moles to grams using the molar mass of MnCl2:
\[{\rm{m}}\;{\rm{(MnC}}{{\rm{l}}_{\rm{2}}}{\rm{)}}\;{\rm{ = }}\;{\rm{0}}{\rm{.645}}\;{\rm{mol}}\;{\rm{ \times }}\;\frac{{{\rm{125}}{\rm{.8}}\;{\rm{g}}}}{{{\rm{1}}\;{\rm{mol}}}}\;{\rm{ = }}\;{\rm{81}}{\rm{.1}}\;{\rm{g}}\]
Percent Yield
21. In a chemistry experiment, a student obtained 5.68 g of a product. What is the percent yield of the product if the theoretical yield was 7.12 g?
79.8 %
The percent yield of the reaction is the ratio of the actual over the theoretical yield. What we obtain is the actual yield and the maximum amount of product that can be obtained from the given amount of the limiting reactant is the theoretical yield.
So, in this example, the actual yield is 5.68 g, and the theoretical yield is 7.12 g.
\[{\rm{\% }}\;{\rm{Yield}}\;{\rm{ = }}\;\frac{{\rm{A}}}{{\rm{T}}}\;{\rm{ = }}\;\frac{{{\rm{5}}{\rm{.68}}\;{\rm{g}}}}{{{\rm{7}}{\rm{.12}}\;{\rm{g}}}}\; \times \;100\% \; = \;79.8\;\% \]
When 38.45 g CCl4 is reacted with an excess of HF, 21.3 g CCl2F2 is obtained. Calculate the theoretical and percent yields of this reaction.
CCl4 + 2HF → CCl2F2 + 2HCl
30.2 g
70.5 %
To find the theoretical yield, we need to calculate the moles of CCl4 and, using the mole ratio, determine how much CCl2F2 can be formed.
\[{\rm{n}}\;{\rm{(CC}}{{\rm{l}}_{\rm{4}}}{\rm{)}}\;{\rm{ = }}\;{\rm{38}}{\rm{.45}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{153}}{\rm{.8}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.250}}\;{\rm{mol}}\]
The amount of CCl2F2 that can be formed from this is also 0.250 mol because of the 1:1 molar ratio:
\[{\rm{n}}\;\left( {{\rm{CC}}{{\rm{l}}_{\rm{2}}}{{\rm{F}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.25 }}\cancel{{{\rm{mol}}\;{\rm{CC}}{{\rm{l}}_{\rm{4}}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}\;{\rm{CC}}{{\rm{l}}_{\rm{2}}}{{\rm{F}}_{\rm{2}}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{CC}}{{\rm{l}}_{\rm{4}}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.25}}\;{\rm{mol}}\]
The mass, which is also the theoretical yield of CCl2F2 is:
\[{\rm{m}}\;{\rm{(CC}}{{\rm{l}}_{\rm{2}}}{{\rm{F}}_{\rm{2}}}{\rm{)}}\;{\rm{ = }}\;{\rm{0}}{\rm{.250}}\;{\rm{mol}}\;{\rm{ \times }}\;\frac{{{\rm{120}}{\rm{.9}}\;{\rm{g}}}}{{{\rm{1}}\;{\rm{mol}}}}\;{\rm{ = }}\;{\rm{30}}{\rm{.2}}\;{\rm{g}}\]
The percent yield of the reaction is the ratio of the actual over the theoretical yield:
\[{\rm{\% }}\;{\rm{Yield}}\;{\rm{ = }}\;\frac{{\rm{A}}}{{\rm{T}}}\;{\rm{ = }}\;\frac{{{\rm{21}}{\rm{.3}}\;{\rm{g}}}}{{{\rm{30}}{\rm{.2}}\;{\rm{g}}}}\; \times \;100\% \; = \;70.5\;\% \]
Iron(III) oxide reacts with carbon monoxide according to the equation:
Fe2O3(s) + 3CO(g) → 2Fe(s) + 3CO2(g)
What is the percent yield of this reaction if 623 g of iron oxide produces 341 g of iron?
78.4%
The actual yield of the reaction is given as 341 g Fe so, to determine the percent yield, we need to first calculate the theoretical yield. This is the amount of Fe that can be formed if all the starting material (in this case Fe2O3) converts into a product according to the chemical equation.
So, we are going to calculate the moles of 623 g Fe2O3 and determine the moles and the mass of the iron based on the stoichiometric ratio:
\[{\rm{n}}\;{\rm{(F}}{{\rm{e}}_{\rm{2}}}{{\rm{O}}_{\rm{3}}}{\rm{)}}\;{\rm{ = }}\;{\rm{623}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{159}}{\rm{.7}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{3}}{\rm{.90}}\;{\rm{mol}}\]
The amount of Fe that can be formed from this is calculated using the mole ratio of the oxide and iron:
\[{\rm{n}}\;\left( {{\rm{Fe}}} \right)\;{\rm{ = }}\;{\rm{3}}{\rm{.90 }}\cancel{{{\rm{mol}}\;{\rm{F}}{{\rm{e}}_{\rm{2}}}{{\rm{O}}_{\rm{3}}}}}\;{\rm{ \times }}\;\frac{{{\rm{2}}\;{\rm{mol}}\;{\rm{Fe}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{F}}{{\rm{e}}_{\rm{2}}}{{\rm{O}}_{\rm{3}}}}}}}\;{\rm{ = }}\;{\rm{7}}{\rm{.80}}\;{\rm{mol}}\]
The mass, which is also the theoretical yield of Fe is:
\[{\rm{m}}\;{\rm{(Fe)}}\;{\rm{ = }}\;{\rm{7}}{\rm{.80}}\;{\rm{mol}}\;{\rm{ \times }}\;\frac{{{\rm{55}}{\rm{.8}}\;{\rm{g}}}}{{{\rm{1}}\;{\rm{mol}}}}\;{\rm{ = }}\;{\rm{435}}\;{\rm{g}}\]
The percent yield of the reaction is the ratio of the actual over the theoretical yield:
\[{\rm{\% }}\;{\rm{Yield}}\;{\rm{ = }}\;\frac{{\rm{A}}}{{\rm{T}}}\;{\rm{ = }}\;\frac{{{\rm{341}}\;{\rm{g}}}}{{{\rm{435}}\;{\rm{g}}}}\; \times \;100\% \; = \;78.4\;\% \]
Determine the percent yield of the reaction if 77.0 g of CO2 are formed from burning 2.00 moles of C5H12 in 4.00 moles of O2.
C5H12 + 8 O2 → 5CO2 + 6H2O
70.0 %
When the amount of both reactants is given, you must determine the LR and then, based on the moles of the LR, determine the amount of product(s) that can be formed. This would be the theoretical yield of CO2.
Now, we are given the moles of the reactants, so we calculate how much CO2 can each produce:
\[{\rm{n}}\;\left( {{\rm{C}}{{\rm{O}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{2}}{\rm{.00 }}\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}}}\;{\rm{ \times }}\;\frac{{{\rm{5}}\;{\rm{mol}}\;{\rm{C}}{{\rm{O}}_{\rm{2}}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{{\rm{C}}_{\rm{5}}}{{\rm{H}}_{{\rm{12}}}}}}}}\;{\rm{ = }}\;{\rm{10}}{\rm{.0}}\;{\rm{mol}}\]
\[{\rm{n}}\;\left( {{\rm{C}}{{\rm{O}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{4}}{\rm{.00 }}\cancel{{{\rm{mol}}\;{{\rm{O}}_{\rm{2}}}}}\;{\rm{ \times }}\;\frac{{{\rm{5}}\;{\rm{mol}}\;{\rm{C}}{{\rm{O}}_{\rm{2}}}}}{{{\rm{8}}\;\cancel{{{\rm{mol}}\;{{\rm{O}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{2}}{\rm{.50}}\;{\rm{mol}}\]
Because oxygen gives less product, it is the LR, and therefore, 2.50 mol CO2 could be formed in this reaction. This is the theoretical yield which is grams is:
\[{\rm{m}}\;{\rm{(C}}{{\rm{O}}_{\rm{2}}}{\rm{)}}\;{\rm{ = }}\;{\rm{2}}{\rm{.50}}\;{\rm{mol}}\;{\rm{ \times }}\;\frac{{{\rm{44}}{\rm{.0}}\;{\rm{g}}}}{{{\rm{1}}\;{\rm{mol}}}}\;{\rm{ = }}\;{\rm{110}}{\rm{.}}\;{\rm{g}}\]
The percent yield of the reaction is the ratio of the actual over the theoretical yield:
\[{\rm{\% }}\;{\rm{Yield}}\;{\rm{ = }}\;\frac{{\rm{A}}}{{\rm{T}}}\;{\rm{ = }}\;\frac{{{\rm{77}}{\rm{.0}}\;{\rm{g}}}}{{{\rm{110}}{\rm{.}}\;{\rm{g}}}}\; \times \;100\% \; = \;70.0\;\% \]
The percent yield for the following reaction was determined to be 84%:
N2(g) + 2H2(g) → N2H4(l)
How many grams of hydrazine (N2H4) can be produced when 38.36 g of nitrogen reacts with 6.68 g of hydrogen?
36.8 g
The problem asks us to find the actual yield of the reaction given that the percent yield is 80%.
When the amounts of both reactants are given, you must determine the LR and then, based on the moles of the LR, determine the amount of product(s) that can be formed. This would be the theoretical yield of hydrazine, and we can use it with the percent yield to find the actual yield of the reaction.
\[{\rm{n}}\;{\rm{(}}{{\rm{N}}_{\rm{2}}}{\rm{)}}\;{\rm{ = }}\;{\rm{38}}{\rm{.36}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{28}}{\rm{.0}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{1}}{\rm{.37}}\;{\rm{mol}}\]
\[{\rm{n}}\;{\rm{(}}{{\rm{H}}_{\rm{2}}}{\rm{)}}\;{\rm{ = }}\;{\rm{6}}{\rm{.68}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{2}}{\rm{.00}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{3}}{\rm{.34}}\;{\rm{mol}}\]
Now, we are given the moles of the reactants, so we calculate how much N2H4 can each produce:
\[{\rm{n}}\;\left( {{{\rm{N}}_{\rm{2}}}{{\rm{H}}_{\rm{4}}}} \right)\;{\rm{ = }}\;{\rm{1}}{\rm{.37 }}\cancel{{{\rm{mol}}\;{{\rm{N}}_{\rm{2}}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}\;{{\rm{N}}_{\rm{2}}}{{\rm{H}}_{\rm{4}}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{{\rm{N}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{1}}{\rm{.37}}\;{\rm{mol}}\]
\[{\rm{n}}\;\left( {{{\rm{N}}_{\rm{2}}}{{\rm{H}}_{\rm{4}}}} \right)\;{\rm{ = }}\;{\rm{3}}{\rm{.34 }}\cancel{{{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}\;{{\rm{N}}_{\rm{2}}}{{\rm{H}}_{\rm{4}}}}}{{{\rm{2}}\;\cancel{{{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{1}}{\rm{.67}}\;{\rm{mol}}\]
N2 gives less hydrazine so, it is the LR, and therefore the theoretical yield of N2H4 is 1.37 mol. The mass of N2H4 is:
\[{\rm{m}}\;{\rm{(}}{{\rm{N}}_{\rm{2}}}{{\rm{H}}_{\rm{4}}}_{\rm{2}}{\rm{)}}\;{\rm{ = }}\;{\rm{1}}{\rm{.37}}\;{\rm{mol}}\;{\rm{ \times }}\;\frac{{{\rm{32}}{\rm{.0}}\;{\rm{g}}}}{{{\rm{1}}\;{\rm{mol}}}}\;{\rm{ = }}\;{\rm{43}}{\rm{.8}}\;{\rm{g}}\]
The percent yield of the reaction is the ratio of the actual over the theoretical yield, so rearranging this equation we can calculate the actual yield:
\[{\rm{\% }}\;{\rm{Yield}}\;{\rm{ = }}\;\frac{{\rm{A}}}{{\rm{T}}}\;\]
A = T x % Yield
A = 43.8 x 0.84 = 36.8 g
Another approach for determining the actual yield is to convert the moles of limiting reactant to the percentage of the percent yield. So, if the yield is 84%, we could have multiplied the moles of N2 by 0.84 and determine the mass of N2H4 based on that.
We would have 1.37 mole x 0.84 = 1.1508 mol N2 which is the moles of nitrogen that actually convert into hydrazine. By the mole ratio, the moles of N2H4 would be:
\[{\rm{n}}\;\left( {{{\rm{N}}_{\rm{2}}}{{\rm{H}}_{\rm{4}}}} \right)\;{\rm{ = }}\;{\rm{1}}{\rm{.1508 }}\cancel{{{\rm{mol}}\;{{\rm{N}}_{\rm{2}}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}\;{{\rm{N}}_{\rm{2}}}{{\rm{H}}_{\rm{4}}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{{\rm{N}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{1}}{\rm{.1508}}\;{\rm{mol}}\]
And the mass would be:
\[{\rm{m}}\;{\rm{(}}{{\rm{N}}_{\rm{2}}}{{\rm{H}}_{\rm{4}}}_{\rm{2}}{\rm{)}}\;{\rm{ = }}\;{\rm{1}}{\rm{.1508}}\;{\rm{mol}}\;{\rm{ \times }}\;\frac{{{\rm{32}}{\rm{.0}}\;{\rm{g}}}}{{{\rm{1}}\;{\rm{mol}}}}\;{\rm{ = }}\;{\rm{36}}{\rm{.8}}\;{\rm{g}}\]
Silver metal can be prepared by reducing its nitrate, AgNO3 with copper according to the following equation:
Cu(s) + 2AgNO3(aq) → Cu(NO3)2(aq) + 2Ag(s)
What is the percent yield of the reaction if 71.5 grams of Ag was obtained from 132.5 grams of AgNO3 ?
85%
The actual yield of the reaction is given as 71.5 g Ag so, to determine the percent yield, we need to first calculate the theoretical yield. This is the amount of Ag that can be formed if all the starting material (in this case AgNO3) converts into product according to the chemical equation.
So, we are going to calculate the moles of 132.5 g AgNO3 and determine the moles and the mass of the silver based on their stoichiometric ratio:
\[{\rm{n}}\;{\rm{(AgN}}{{\rm{O}}_{\rm{3}}}{\rm{)}}\;{\rm{ = }}\;{\rm{132}}{\rm{.5}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{169}}{\rm{.9}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.780}}\;{\rm{mol}}\]
\[{\rm{n}}\;\left( {{\rm{Ag}}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.780 }}\cancel{{{\rm{mol}}\;{\rm{AgN}}{{\rm{O}}_{\rm{3}}}}}\;{\rm{ \times }}\;\frac{{{\rm{2}}\;{\rm{mol}}\;{\rm{Ag}}}}{{{\rm{2}}\;\cancel{{{\rm{mol}}\;{\rm{AgN}}{{\rm{O}}_{\rm{3}}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.780}}\;{\rm{mol}}\]
The mass, which is also the theoretical yield of Ag is:
\[{\rm{m}}\;{\rm{(Ag)}}\;{\rm{ = }}\;{\rm{0}}{\rm{.780}}\;{\rm{mol}}\;{\rm{ \times }}\;\frac{{{\rm{107}}{\rm{.9}}\;{\rm{g}}}}{{{\rm{1}}\;{\rm{mol}}}}\;{\rm{ = }}\;{\rm{84}}{\rm{.2}}\;{\rm{g}}\]
The percent yield of the reaction is the ratio of the actual over the theoretical yield:
\[{\rm{\% }}\;{\rm{Yield}}\;{\rm{ = }}\;\frac{{\rm{A}}}{{\rm{T}}}\;{\rm{ = }}\;\frac{{{\rm{71}}{\rm{.5}}\;{\rm{g}}}}{{{\rm{84}}{\rm{.2}}\;{\rm{g}}}}\; \times \;100\% \; = \;85\;\% \]
Industrially, nitric acid is produced from ammonia by the Ostwald process in a series of reactions:
4NH3(g) + 5O2(g) → 4NO(g) + 6H2O(l)
2NO(g) + O2(g) → 2NO2(g)
2NO2(g) + H2O(l) → HNO3(aq) + HNO2(aq)
Considering that each reaction has an 85% percent yield, how many grams of NH3 must be used to produce 25.0 kg of HNO3 by the above procedure?
2.20 x 104 g
Because we are given the mass of the product and need to determine the mass of the starting material, the calculations are going to be in reverse order. So, first, we can calculate the moles of HNO3 and using the mole ratio, find the moles of NO2 which is the link between the 3rd and 2nd reactions.
Before using the mass of HNO3, convert it to grams because the molar mass is given in grams per mole:
\[{\rm{m}}\left( {{\rm{HN}}{{\rm{O}}_{\rm{3}}}} \right)\;{\rm{ = }}\;{\rm{25}}{\rm{.0}}\;\cancel{{{\rm{kg}}}}\;{\rm{ \times }}\;\frac{{{\rm{1000}}\;{\rm{g}}}}{{{\rm{1}}\;\cancel{{{\rm{kg}}}}}}\;{\rm{ = }}\;{\rm{2}}{\rm{.5}}\;{\rm{ \times }}\;{\rm{1}}{{\rm{0}}^{\rm{4}}}\;{\rm{g}}\]
\[{\rm{n}}\;{\rm{(HN}}{{\rm{O}}_{\rm{3}}}{\rm{)}}\;{\rm{ = }}\;{\rm{2}}{\rm{.50}}\;{\rm{ \times }}\;{10^4}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{63}}{\rm{.0}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{397}}\;{\rm{mol}}\]
\[{\rm{n}}\;\left( {{\rm{N}}{{\rm{O}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{397 }}\cancel{{{\rm{mol}}\;{\rm{HN}}{{\rm{O}}_{\rm{3}}}}}\;{\rm{ \times }}\;\frac{{{\rm{2}}\;{\rm{mol}}\;{\rm{N}}{{\rm{O}}_{\rm{2}}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{HN}}{{\rm{O}}_{\rm{3}}}}}}}\;{\rm{ = }}\;{\rm{794}}\;{\rm{mol}}\]
Now, this would have been the conversion if it was a process with a 100% yield. However, because each step of this process has an 85% percent yield, we need to multiply each mole conversion by a factor of
\[\frac{{{\rm{100\% }}}}{{{\rm{85\% }}}}\;{\rm{or}}\;{\rm{simply}}\;\frac{{{\rm{100}}}}{{{\rm{85}}}}\]
So, the moles of NO2 that produced 397 mol of HNO3 would be:
\[{\rm{n}}\;\left( {{\rm{N}}{{\rm{O}}_{\rm{2}}}} \right)\;{\rm{ = }}\;{\rm{794}}\;{\rm{mol}}\;{\rm{ \times }}\;\frac{{{\rm{100}}}}{{{\rm{85}}}}\;{\rm{ = }}\;{\rm{934}}\;{\rm{mol}}\]
Now, we go to the second reaction and see how much NO was needed to produce 934 mol NO2 considering that the yield of the reaction is again 85%.
2NO(g) + O2(g) → 2NO2(g)
\[{\rm{n}}\;\left( {{\rm{NO}}} \right)\;{\rm{ = }}\;{\rm{934 }}\cancel{{{\rm{mol}}\;{\rm{N}}{{\rm{O}}_{\rm{2}}}}}\;{\rm{ \times }}\;\frac{{{\rm{2}}\;{\rm{mol}}\;{\rm{NO}}}}{{{\rm{2}}\;\cancel{{{\rm{mol}}\;{\rm{N}}{{\rm{O}}_{\rm{2}}}}}}}\; \times \;\frac{{100}}{{85}}\;{\rm{ = }}\;{\rm{1098}}\;{\rm{mol}}\]
Next, we do the same for the first reaction and determine how much NH3 was needed to produce 1098 mol NO considering that the yield of the reaction is again 85%.
4NH3(g) + 5O2(g) → 4NO(g) + 6H2O(l)
\[{\rm{n}}\;\left( {{\rm{N}}{{\rm{H}}_{\rm{3}}}} \right)\;{\rm{ = }}\;{\rm{1098 }}\cancel{{{\rm{mol}}\;{\rm{NO}}}}\;{\rm{ \times }}\;\frac{{{\rm{4}}\;{\rm{mol}}\;{\rm{N}}{{\rm{H}}_{\rm{3}}}}}{{{\rm{4}}\;\cancel{{{\rm{mol}}\;{\rm{NO}}}}}}\;{\rm{ \times }}\;\frac{{{\rm{100}}}}{{{\rm{85}}}}\;{\rm{ = }}\;{\rm{1293}}\;{\rm{mol}}\]
In the last step, we convert the moles to the mass of ammonia:
\[{\rm{m}}\;{\rm{(N}}{{\rm{H}}_{\rm{3}}}{\rm{)}}\;{\rm{ = }}\;{\rm{1293}}\;{\rm{mol}}\;{\rm{ \times }}\;\frac{{{\rm{17}}{\rm{.0}}\;{\rm{g}}}}{{{\rm{1}}\;{\rm{mol}}}}\;{\rm{ = }}\;{\rm{21,981}}\;{\rm{g}}\]
Rounding off to three significant figures, we get:
2.20 x 104 g
Aspirin (acetylsalicylic acid) is widely used to treat pain, fever, and inflammation. It is produced from the reaction of salicylic acid with acetic anhydride. The chemical equation for aspirin synthesis is shown below:
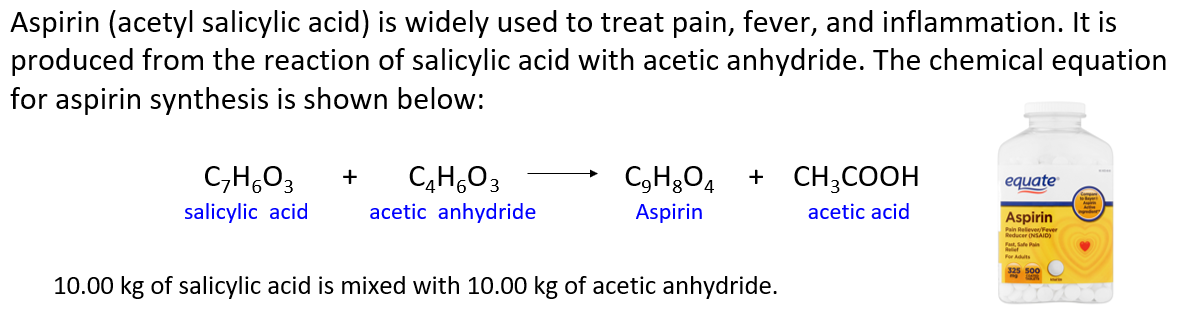
In one container, 10.00 kg of salicylic acid is mixed with 10.00 kg of acetic anhydride.
a) Which reactant is limiting? Which is in excess?
b) What mass of excess reactant is left over?
c) What mass of aspirin is formed assuming 100% yield (Theoretical yield)?
d) What mass of aspirin is formed if the reaction yield is 70.0% ?
e) If the actual yield of aspirin is 11.2 kg, what is the percent yield?
f) How many kg of salicylic acid is needed to produce 20.0 kg of aspirin if the reaction yield is 85.0% ?
Salicylic acid is the limiting reagent
2.608 x 103 g Acetic anhydride
1.305 x 104 g Aspirin
9.14 x 103 g Aspirin
85.8 %
18.1 kg
a) Which reactant is limiting? Which is in excess?
The limiting reactant is the one producing less product, so we need to calculate the moles of 00 kg salicylic acid and 10.00 kg acetic anhydride and see which one produces less aspirin. Because the mole ratio of all the reactants and products is 1:1, whichever has a smaller number of moles, it is the limiting reactant.
Before using the masses, convert them to grams because the molar mass is given in grams per mole:
\[{\rm{m}}\left( {{\rm{salicylic acid}}} \right)\;{\rm{ = }}\;{\rm{10}}{\rm{.00}}\;\cancel{{{\rm{kg}}}}\;{\rm{ \times }}\;\frac{{{\rm{1000}}\;{\rm{g}}}}{{{\rm{1}}\;\cancel{{{\rm{kg}}}}}}\;{\rm{ = }}\;{\rm{1}}{\rm{.000}}\;{\rm{ \times }}\;{\rm{1}}{{\rm{0}}^{\rm{4}}}\;{\rm{g}}\]
\[{\rm{m}}\left( {{\rm{acetic anhydride}}} \right)\;{\rm{ = }}\;{\rm{10}}{\rm{.00}}\;\cancel{{{\rm{kg}}}}\;{\rm{ \times }}\;\frac{{{\rm{1000}}\;{\rm{g}}}}{{{\rm{1}}\;\cancel{{{\rm{kg}}}}}}\;{\rm{ = }}\;{\rm{1}}{\rm{.000}}\;{\rm{ \times }}\;{\rm{1}}{{\rm{0}}^{\rm{4}}}\;{\rm{g}}\]
\[{\rm{n}}\;{\rm{(salicylic acid)}}\;{\rm{ = }}\;{\rm{1}}{\rm{.000}}\;{\rm{ \times }}\;{\rm{1}}{{\rm{0}}^{\rm{4}}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{138}}{\rm{.1}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{72}}{\rm{.4}}\;{\rm{mol}}\]
\[{\rm{n}}\;{\rm{(acetic anhydride)}}\;{\rm{ = }}\;{\rm{1}}{\rm{.000}}\;{\rm{ \times }}\;{\rm{1}}{{\rm{0}}^{\rm{4}}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{102}}{\rm{.1}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{97}}{\rm{.9}}\;{\rm{mol}}\]
Salicylic acid is present in a smaller quantity, and because of the 1:1 molar ratio of all the reactants and products, it is going to produce less aspirin, and therefore, it is the limiting reactant.
b) What mass of excess reactant is left over?
We know that salicylic acid is the limiting reactant, so the calculations are going to be based on its moles (72.4 mol). Using the mole ratio, we can calculate how much acetic anhydride has reacted. The remaining mass of the acetic anhydride is calculated by subtracting this amount from the initial mass.
Again, because of the 1:1 molar ratio, there is going to be 72.4 mol acetic anhydride reacted:
\[{\rm{n}}\;\left( {{\rm{acetic anhydride}}} \right)\;{\rm{ = }}\;{\rm{72}}{\rm{.4 }}\cancel{{{\rm{mol}}\;{\rm{salicylic acid}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}\;{\rm{acetic anhydride}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{salicylic acid}}}}}}\;{\rm{ = }}\;{\rm{72}}{\rm{.4}}\;{\rm{mol}}\]
This corresponds to:
\[{\rm{m}}\;{\rm{(acetic anhydride)}}\;{\rm{ = }}\;{\rm{72}}{\rm{.4}}\;{\rm{mol}}\;{\rm{ \times }}\;\frac{{{\rm{102}}{\rm{.1}}\;{\rm{g}}\;}}{{{\rm{1}}\;{\rm{mol}}}}\;{\rm{ = }}\;{\rm{7392}}\;{\rm{g}}\]
The remaining mass of acetic anhydride is:
10,000 – 7392 = 2608 g = 2.608 kg
c) What mass of aspirin is formed assuming 100% yield (Theoretical yield)?
72.4 mol aspirin will be formed because of the 1:1 molar ratio:
\[{\rm{n}}\;\left( {{\rm{aspirin}}} \right)\;{\rm{ = }}\;{\rm{72}}{\rm{.4 }}\cancel{{{\rm{mol}}\;{\rm{salicylic acid}}}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}\;{\rm{aspirin}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{salicylic acid}}}}}}\;{\rm{ = }}\;{\rm{72}}{\rm{.4}}\;{\rm{mol}}\]
Using the molar mass of aspirin, we can calculate its mass for 100%-yield reaction:
\[{\rm{m}}\;{\rm{(aspirin)}}\;{\rm{ = }}\;{\rm{72}}{\rm{.4}}\;{\rm{mol}}\;{\rm{ \times }}\;\frac{{{\rm{180}}{\rm{.2}}\;{\rm{g}}}}{{{\rm{1}}\;{\rm{mol}}}}\;{\rm{ = }}\;{\rm{13,046}}\;{\rm{g}}\]
This corresponds to 13.05 kg when divided by 1000.
d) What mass of aspirin is formed if the reaction yield is 70.0%?
To find the mass of aspirin when the percent yield is 70.0%, we need to multiply the theoretical yield (13.05 kg) by 0.700:
m (aspirin) = 13.05 kg x 0.700 = 9.14 kg
e) If the actual yield of aspirin is 11.2 kg, what is the percent yield?
The percent yield of the reaction is the ratio of the actual over the theoretical yield:
\[{\rm{\% }}\;{\rm{Yield}}\;{\rm{ = }}\;\frac{{\rm{A}}}{{\rm{T}}}\;{\rm{ = }}\;\frac{{{\rm{11}}{\rm{.2}}\;{\rm{kg}}}}{{{\rm{13}}{\rm{.05}}\;{\rm{kg}}}}\;{\rm{ \times }}\;{\rm{100\% }}\;{\rm{ = }}\;{\rm{85}}{\rm{.8}}\;{\rm{\% }}\]
f) How many kg of salicylic acid is needed to produce 20.0 kg of aspirin if the reaction yield is 85.0% ?
First, calculate the moles of 20.0 kg aspirin which is 2.00 x 104 g:
\[{\rm{n}}\;{\rm{(aspirin)}}\;{\rm{ = }}\;{\rm{2}}{\rm{.0}}\;{\rm{ \times }}\;{\rm{1}}{{\rm{0}}^{\rm{4}}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{180}}{\rm{.2}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{111}}\;{\rm{mol}}\]
According to the mole ratio of the chemical equation, this is how much salicylic acid would be needed because of the 1:1 mole ratio.
However, because the reaction has an 85.0% percent yield, we need to multiply the moles by a factor of
\[{\rm{n}}\;{\rm{(salicylic acid)}}\;{\rm{ = }}\;{\rm{111}}\;{\rm{mol}}\;{\rm{ \times }}\;\frac{{{\rm{100}}}}{{{\rm{85}}}}\;{\rm{ = }}\;{\rm{131}}\;{\rm{mol}}\]
The mass of salicylic acid would be:
\[{\rm{m}}\;{\rm{(salicylic acid)}}\;{\rm{ = }}\;{\rm{131}}\;{\rm{mol}}\;{\rm{ \times }}\;\frac{{{\rm{138}}\;{\rm{g}}}}{{{\rm{1}}\;{\rm{mol}}}}\;{\rm{ = }}\;{\rm{18,078}}\;{\rm{g}}\]
This corresponds to 18.1 kg
You forgot the subscript 3 for O in the molecular formula for acetic anhydride and the reaction is not balanced as written.
For part F) it’s 18.1 kg and not1.81 kg as written in the final line of the solution.
Thanks for letting me know! Fixed.
You’re welcome!