In the previous post, we talked about the limiting reactant and its importance in determining how much product can be produced in a chemical reaction. The amount of product(s) we calculate based on the limiting reactant is called the theoretical yield.
For example, we saw that 1.6 mol of NO can be obtained when 2 mol of NH3 and 2 mol of O2 are reacted according to the following equation:
4NH3 + 5O2 → 4NO + 6H2O
For this, we calculate separately, how many moles of it can 2 mol of NH3 and 2 mol of O2 produce:
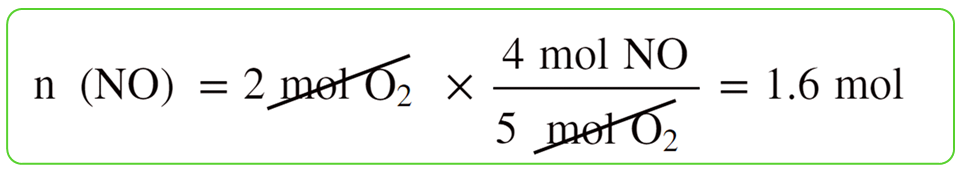
So, this is the theoretical yield that we’d obtain if everything in the reaction worked ideally as written on the paper.
However, most of the time, we do not obtain as much product as the theoretical yield suggests. The amount of product we obtain is the actual yield of the reaction. The theoretical yield and the actual yield of a reaction are often different.
To quantify this difference, the percent yield is used which is the ratio of the actual and theoretical yield multiplied by 100%:
For example: In a chemistry experiment, a student obtained 5.68 g of a product. What is the percent yield of the product if the theoretical yield was 7.12 g?
5.68 g is the actual yield because that is how much material the student obtained. The theoretical yield is 7.12 g which had been calculated based on the limiting reactant.
The percent yield is the ratio of these two:
\[{\rm{\% }}\;{\rm{Yield}}\;{\rm{ = }}\;\frac{{\rm{A}}}{{\rm{T}}}\;{\rm{ = }}\;\frac{{{\rm{10}}{\rm{.68}}\;{\rm{g}}}}{{{\rm{17}}{\rm{.8}}\;{\rm{g}}}}\; \times \;100\% \; = \;60.0\;\% \]
An analogy of the percent yield can be comparing how many people make it to the finish-line of a marathon compared to how many had started it. For example, if 1000 people started the marathon and only 600 made to the end, the yield or the efficiency of the marathon is 60%:
Solving Percent Yield Problems
At this point of studying stoichiometry, we have already learned about molar ratios, stoichiometric calculations based on these ratios, limiting reactant, and the percent yield.
Follow these steps to determine the percent yield or, in general, working on stoichiometry problems:
1) Determine the moles of reactants
2) Determine the limiting reagent
3) Determine the theoretical yield
4) Determine the reaction/percent yield
For example: What is the yield of the reaction if 10.68 g sulfur was obtained by reacting 12.6 g H2S with 14.6 g SO2 according to the following equation?
2H2S(g) + SO2(g) → 3S(s) + 2H2O(g)
1) Determine the moles of reactants:
\[{\rm{n}}\;{\rm{(}}{{\rm{H}}_{\rm{2}}}{\rm{S)}}\;{\rm{ = }}\;{\rm{12}}{\rm{.6}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{34}}{\rm{.1}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.370}}\;{\rm{mol}}\]
\[{\rm{n}}\;{\rm{(S}}{{\rm{O}}_{\rm{2}}}{\rm{)}}\;{\rm{ = }}\;{\rm{14}}{\rm{.6}}\;{\rm{g}}\;{\rm{ \times }}\;\frac{{{\rm{1}}\;{\rm{mol}}}}{{{\rm{64}}{\rm{.1}}\;{\rm{g}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.228}}\;{\rm{mol}}\]
2) Determine the limiting reagent:
\[{\rm{n}}\;\left( {\rm{S}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.370 }}\cancel{{{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}{\rm{S}}}}\;{\rm{ \times }}\;\frac{{{\rm{3}}\;{\rm{mol}}\;{\rm{S}}}}{{{\rm{2}}\;\cancel{{{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}{\rm{S}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.555}}\;{\rm{mol}}\]
\[{\rm{n}}\;\left( {\rm{S}} \right)\;{\rm{ = }}\;{\rm{0}}{\rm{.228 }}\cancel{{{\rm{mol}}\;{\rm{S}}{{\rm{O}}_{\rm{2}}}}}\;{\rm{ \times }}\;\frac{{{\rm{3}}\;{\rm{mol}}\;{\rm{S}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{S}}{{\rm{O}}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.684}}\;{\rm{mol}}\]
0.370 mol H2S gives less sulfur and therefore, it is the limiting reactant.
3) Determine the theoretical yield:
H2S gives less S and therefore, it is the LR and 0.555 mol of S is the theoretical yield. The mass of sulfur is:
\[{\rm{m}}\;{\rm{(S)}}\;{\rm{ = }}\;{\rm{0}}{\rm{.555}}\;{\rm{mol}}\;{\rm{ \times }}\;\frac{{{\rm{32}}{\rm{.1}}\;{\rm{g}}}}{{{\rm{1}}\;{\rm{mol}}}}\;{\rm{ = }}\;{\rm{17}}{\rm{.8}}\;{\rm{g}}\]
4) Determine the reaction/percent yield:
\[{\rm{\% }}\;{\rm{Yield}}\;{\rm{ = }}\;\frac{{\rm{A}}}{{\rm{T}}}\;{\rm{ = }}\;\frac{{{\rm{10}}{\rm{.68}}\;{\rm{g}}}}{{{\rm{17}}{\rm{.8}}\;{\rm{g}}}}\; \times \;100\% \; = \;60.0\;\% \]
Check Also
- The Mole and Molar Mass
- Molar Calculations
- Percent Composition and Empirical Formula
- Stoichiometry of Chemical Reactions
- Limiting Reactant
- Reaction/Percent Yield
- Stoichiometry Practice Problems
Practice
What is the theoretical yield of Ca(OH)2, in grams, if 39.27 g of CaO is hydrolyzed (reacted) in an excess of water?
In a chemistry experiment, a student obtained 5.68 g of a product. What is the percent yield of the product if the theoretical yield was 7.12 g?
When 38.45 g CCl4 is reacted with an excess of HF, 21.3 g CCl2F2 is obtained. Calculate the theoretical and percent yields of this reaction.
CCl4 + 2HF → CCl2F2 + 2HCl
Iron(III) oxide reacts with carbon monoxide according to the equation:
Fe2O3(s) + 3CO(g) → 2Fe(s) + 3CO2(g)
What is the percent yield of this reaction if 623 g of iron oxide produces 341 g of iron?
Determine the percent yield of the reaction if 77.0 g of CO2 are formed from burning 2.00 moles of C5H12 in 4.00 moles of O2.
C5H12 + 8 O2 → 5CO2 + 6H2O
The percent yield for the following reaction was determined to be 84%:
N2(g) + 2H2(g) → N2H4(l)
How many grams of hydrazine (N2H4) can be produced when 38.36 g of nitrogen reacts with 6.68 g of hydrogen?
Silver metal can be prepared by reducing its nitrate, AgNO3 with copper according to the following equation:
Cu(s) + 2AgNO3(aq) → Cu(NO3)2(aq) + 2Ag(s)
What is the percent yield of the reaction if 71.5 grams of Ag was obtained from 132.5 grams of AgNO3 ?
Industrially, nitric acid is produced from ammonia by the Ostwald process in a series of reactions:
4NH3(g) + 5O2(g) → 4NO(g) + 6H2O(l)
2NO(g) + O2(g) → 2NO2(g)
2NO2(g) + H2O(l) → HNO3(aq) + HNO2(aq)
Considering that each reaction has an 85% percent yield, how many grams of NH3 must be used to produce 25.0 kg of HNO3 by the above procedure?
Aspirin (acetyl salicylic acid) is widely used to treat pain, fever, and inflammation. It is produced from the reaction of salicylic acid with acetic anhydride. The chemical equation for aspirin synthesis is shown below:
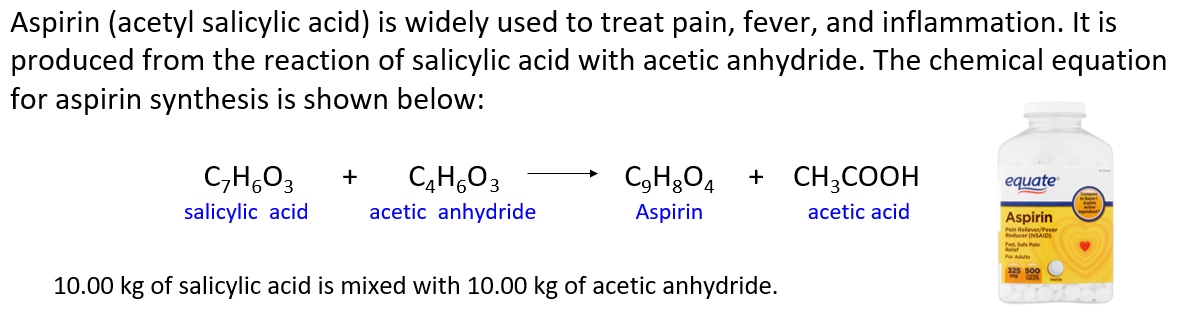
In one container, 10.00 kg of salicylic acid is mixed with 10.00 kg of acetic anhydride.
a) Which reactant is limiting? Which is in excess?
b) What mass of excess reactant is left over?
c) What mass of aspirin is formed assuming 100% yield (Theoretical yield)?
d) What mass of aspirin is formed if the reaction yield is 70.0% ?
e) If the actual yield of aspirin is 11.2 kg, what is the percent yield?
f) How many kg of salicylic acid is needed to produce 20.0 kg of aspirin if the reaction yield is 85.0% ?
Thank you so much! This really helped me a lot and especially the practice problems were helpful to understand the concept.
Good
I somewhat got this
Really very good stuff