Limiting reactant is the one that dictates how much product can be formed. For solving problems, the concept of limiting reactant becomes relevant when the quantities of both (more than one) reactants are given.

As an example, to illustrate this, let’s consider a situation where five people need to take a seat but there are only four chairs available.

This is a simple example where we’d easily agree that the number of chairs or simply the chair is the limiting component.

Transferring this to a chemical reaction let’s consider the reaction between 5 mol NaOH and 3 mol HCl:

NaOH + HCl   →  NaCl + H₂O

Here again, we can see that the HCl is the limiting reactant because there is not enough of it to react with 5 mol NaOH. NaOH is said to be in excess which means there is more than enough of it to consume all the HCl, and some of it will still remain after the reaction is complete.

So, remember, if the reactants are not in stoichiometric ratio, one of them is the limiting reactant (LR), and the other is in excess.

Limiting Reactant When the Ratio is Not 1:1

Determining the limiting reactant becomes a little more challenging when the mole-rations of the reactants is not 1:1. In this case, we cannot determine the limiting reactant just by looking at the initial amounts of the reactants.

For example, determine the limiting reactant when 1 mole of PCl₅ is reacted with 3 moles of water:

PCl₅ + 4H₂O → H₃PO₄ + 5HCl

It may seem like PCl₅ is the limiting reactant because there is only 1 mole of it compared to 3 moles of water, however, it turns out that the water is the limiting reactant.

So, how is the reactant in larger quantity the limiting reactant?

This is due to the 1:4 mole ratio which indicates that there is always going to be four times more water required to react with any amount of PCl_5.

To illustrate this concept let’s consider the ratio of wheel and body for building a car. Every vehicle requires one body and four wheels.

So, if there is one body and three wheels, the wheels are the limiting factor because you would need to have four of them and only one body to build one vehicle:

And if we had, for example, 7 wheels and one body, there will be enough wheels to produce one vehicle, but not enough for making two. So, in this case, as well, the wheels are the limiting factor, even though they are in a larger quantity:

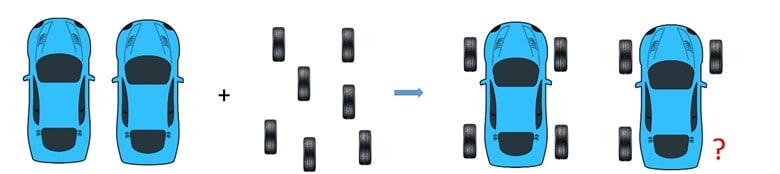
These examples tell an important message to keep in mind: we cannot look at the moles of the reactants and determine which one is the limiting reactant. The limiting reactant is the one that produces less product and not necessarily the one that is present in fewer amounts.

The correct approach is to calculate the moles of both reactants and, using molar conversions, determine which one produces less product.

Now, going back to the reaction of 1 mole of PCl₅ and 3 moles of water, we need to pick a product and determine which of the reactants will produce less of that product.

You can use any of the products for your calculations, but it must be the same for both reactants. Check this article on the stoichiometry of chemical reactions to refresh the concept of mole-to-mole conversions based on the coefficients of the reactants and products. 

Let’s do the calculations for H₃PO₄:

PCl₅ + 4 H₂O → H₃PO₄ + 5 HCl

The amount of H₃PO₄ produced from 1 mole PCl₅ is:

\[{\rm{n}}\;{\rm{(}}{{\rm{H}}_{\rm{3}}}{\rm{P}}{{\rm{O}}_{\rm{4}}}{\rm{)}}\;{\rm{ = }}\;{\rm{1}}\;\cancel{{{\rm{mol PC}}{{\rm{l}}_{\rm{5}}}}}{\rm{ }} \times \;\frac{{{\rm{1}}\;{\rm{mol}}\;{{\rm{H}}_{\rm{3}}}{\rm{P}}{{\rm{O}}_{\rm{4}}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\,{\rm{PC}}{{\rm{l}}_{\rm{5}}}}}}}\; = \;{\rm{1}}\;{\rm{mol }}{{\rm{H}}_{\rm{3}}}{\rm{P}}{{\rm{O}}_{\rm{4}}}\]

The amount of H₃PO₄ produced from 3 moles of water is:

\[{\rm{n}}\;{\rm{(}}{{\rm{H}}_{\rm{3}}}{\rm{P}}{{\rm{O}}_{\rm{4}}}{\rm{)}}\;{\rm{ = }}\;{\rm{3}}\;\cancel{{{\rm{mol }}{{\rm{H}}_{\rm{2}}}{\rm{O}}}}{\rm{  \times }}\frac{{{\rm{1}}\;{\rm{mol}}\;{{\rm{H}}_{\rm{3}}}{\rm{P}}{{\rm{O}}_{\rm{4}}}}}{{{\rm{4}}\;\cancel{{{\rm{mol}}\;{{\rm{H}}_{\rm{2}}}{\rm{O}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.75}}\;{\rm{mol}}\;{{\rm{H}}_{\rm{3}}}{\rm{P}}{{\rm{O}}_{\rm{4}}}\]

3 mol of H₂O produces less H₃PO₄, than 1 mol PCl₅ does and therefore, it is the limiting reactant.

A Shortcut for Determining the Limiting Reactant

A shorter way of determining the limiting reactant is by dividing the moles of reactants by their coefficients.

For example: Determine the limiting reactant when 2 mol of NH₃ and 2 mol of O₂ are reacted as follows:

4NH₃ + 5O₂ → 4NO + 6H₂O

Write the moles on top of each reactant and divide them by the corresponding coefficient:

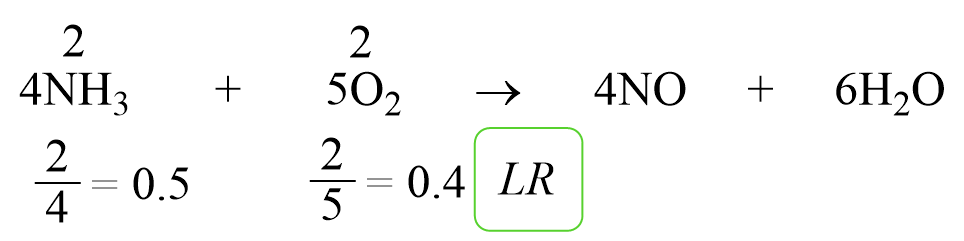
0.4 < 0.5 and as expected, O₂ is the limiting reactant by this method too.

We can confirm this by the standard way of determining the limiting reactant.

Let’s choose NO as the reference and calculate, separately, how many moles of it can 2 mol of NH₃ and 2 mol of O₂ produce:

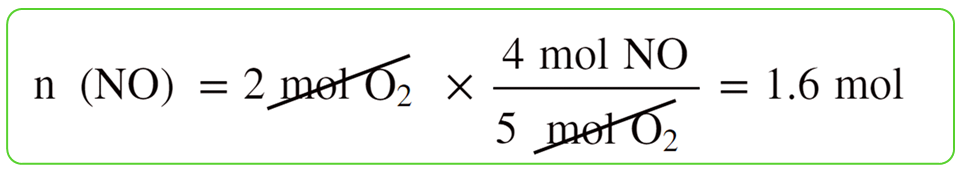
2 mol of O₂ produces less NO, therefore, it is the limiting reactant.

We can put together a short summary for determining the limiting reactant as such:

Check Also

• The Mole and Molar Mass
• How To Calculate The Molar Mass
• How To Convert Grams To Moles
• Grams to Molecules and Molecules to Mass
• How To Convert Grams To Number of Atoms
• Mass, Moles, and Number of Particles Practice
• Percent Composition and Empirical Formula
• Percent Composition and Empirical Formula Practice Problems
• Stoichiometry of Chemical Reactions
• How To Find The Amount of Excess Reactant
• Limiting Reactant Practice Problems
• Reaction/Percent Yield
• Stoichiometry Practice Problems