Stoichiometry

How To Convert Grams To Moles

To convert the grams to moles, we need to know the molar mass of the substance. Remember, molar mass (M) is the mass of one mole of atoms/molecules/ions expressed in g/mol. To calculate it we are always going to need a periodic table. So, how do we find the molar mass in the periodic table?

For example, there are two numbers given for potassium in the periodic table: 19 and 39.098. The smaller one is the atomic number which shows the number of protons, and the larger one is the average atomic mass:

What’s important for today’s topic is that numerically, the molar mass is equal to the average atomic mass of the given atom, so we can look it up in the periodic table. For potassium then, it is 39.098 g/mol which means one mole of potassium atoms weighs 39.098 g. And we can do this for all the elements in the periodic table.

Converting Mass to Moles

To calculate the moles from a given mass (m), the molar mass of the component is used. The given mass is the mass of the sample, and it can be any number, for example, we can have 10 g of salt, 15 g, or 100 g. The molar mass, on the other hand, is a constant number for a given atom or a molecule as it is for a specific amount of it.

So, to calculate the moles from a given mass, we make a conversion factor correlating 1 mole with the molar of the given component.

For example, how many moles of sulfur are there in a 16.2 g sample?

The molar mass of sulfur is 32.1 g/mol, and therefore, the conversion factors are:

\[\frac{{{\rm{1}}\;{\rm{mol}}\;{\rm{S}}}}{{{\rm{32}}{\rm{.1}}\;{\rm{g}}\,{\rm{S}}}}\;\,and\,\,\frac{{{\rm{32}}{\rm{.1}}\;{\rm{g}}\,{\rm{S}}}}{{{\rm{1}}\;{\rm{mol}}\;{\rm{S}}}}\]

These two simply indicate that 1 mol of S weighs 32.1 g, which is the molar mass of the sulfur which we find it in the periodic table.

Now, to calculate the molar mass, we need to choose the correct conversion factor. Remember, the idea is to choose the one that allows to cancel the gram units. So, it should be the one where the grams are in the denominator.

Once you determine the correct conversion factor, multiply the numbers and cancel out the units:

There is also a formula correlating the number of moles with the molar mass (M) and the given mass (m). So, you can also use this formula when converting between mass, molar mass, and moles:

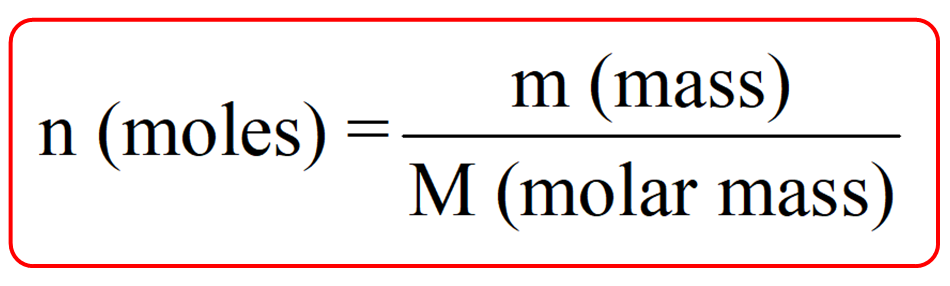
For our example of 13.2 g sulfur, we’d have:

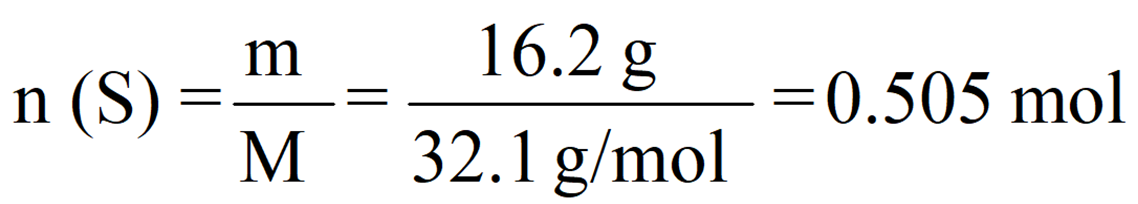
Notice that the exact answer in the calculator is 0.5046728 and we round it off to three significant figures because both initial numbers contain three significant figures.

Moles of Molecules from the Mass

To calculate the moles of a molecule, from the given mass, we are following the same steps as we did for the atom. The only difference is that the molar mass of the molecule is not going to be given in the periodic table, so you will need to calculate it first.

To calculate the molar mass of a molecule, we add the molar mass of each constituent atom by the corresponding subscript.

For example, the molar mass of water would be:

M (H₂O) = 2 x 1.0 + 16.0 = 18.0 g/mol

If the formula of the molecule is not given, you will need to first determine it.

For example, determine the molar mass of phosphorous pentachloride.

The formula of phosphorous pentachloride is PCl₅. Go over naming covalent compounds to refresh some of the concepts here.

To calculate the molar mass of PCl₅, we multiply the molar mass of each element by its subscript:

M (PCl₅) = M (P) + 5x M (Cl)

M (PCl₅) = 30.1 + 5 x 35.5 = 207.6 g/mol

Another example: what is the molar mass of aluminum sulfate?

First, we know that the aluminum ion has a 3+ charge. You need to know the common polyatomic ions from where we find that sulfate is the SO₄^2- ion. Next, we write the ions next to each other and add the correct subscripts:

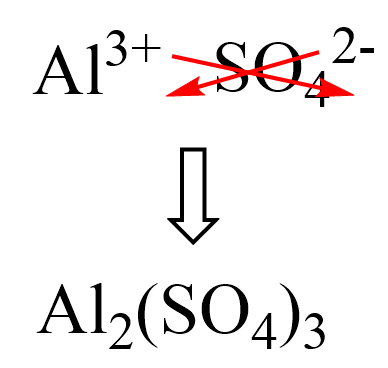
And now, we multiply the molar mass of each element by its subscript. Remember, the number outside of parenthesis applies to all the elements in it.

M (Al₂(SO₄)₃) = 2 x M (Al) + 3 x M (S) + 3 x 4 x M (O)

M (Al₂(SO₄)₃) = 2 x 27.0 + 3 x 32.1 + 3 x 4 x 16.0 = 342.3 g/mol

We have calculated the molar mass of Al₂(SO₄)_3,so let’s say we need to determine the number of moles in a 78.1 g sample.

The conversion factors are:

\[\frac{{{\rm{1}}\;{\rm{mol}}\;{\rm{A}}{{\rm{l}}_{\rm{2}}}{{{\rm{(S}}{{\rm{O}}_{\rm{4}}}{\rm{)}}}_{\rm{3}}}}}{{342.3\;{\rm{g}}\,{\rm{A}}{{\rm{l}}_{\rm{2}}}{{{\rm{(S}}{{\rm{O}}_{\rm{4}}}{\rm{)}}}_{\rm{3}}}}}\;\,or\,\,\frac{{342.3\;{\rm{g}}\,{\rm{A}}{{\rm{l}}_{\rm{2}}}{{{\rm{(S}}{{\rm{O}}_{\rm{4}}}{\rm{)}}}_{\rm{3}}}}}{{{\rm{1}}\;{\rm{mol}}\;{\rm{A}}{{\rm{l}}_{\rm{2}}}{{{\rm{(S}}{{\rm{O}}_{\rm{4}}}{\rm{)}}}_{\rm{3}}}}}\]

We are starting with grams, and therefore, the first conversion factor is correct as it will allow us to cancel the gram units:

\[{\rm{n}}\,{\rm{ = }}\,{\rm{78}}{\rm{.1}}\,\cancel{{{\rm{g}}\,{\rm{A}}{{\rm{l}}_{\rm{2}}}{{{\rm{(S}}{{\rm{O}}_{\rm{4}}}{\rm{)}}}_{\rm{3}}}}}{\rm{ \times }}\,\frac{{{\rm{1}}\;{\rm{mol}}\;{\rm{A}}{{\rm{l}}_{\rm{2}}}{{{\rm{(S}}{{\rm{O}}_{\rm{4}}}{\rm{)}}}_{\rm{3}}}}}{{{\rm{342}}{\rm{.3}}\;\cancel{{{\rm{g}}\,{\rm{A}}{{\rm{l}}_{\rm{2}}}{{{\rm{(S}}{{\rm{O}}_{\rm{4}}}{\rm{)}}}_{\rm{3}}}}}}}\,{\rm{ = }}\,{\rm{0}}{\rm{.228}}\;{\rm{mol}}\,{\rm{A}}{{\rm{l}}_{\rm{2}}}{{\rm{(S}}{{\rm{O}}_{\rm{4}}}{\rm{)}}_{\rm{3}}}\]

Moles of a Specific Atom

Sometimes you may be asked to calculate the moles of a specific atom given the mass of a compound. For example, how many moles of nitrogen atoms are there in 46.0 g sample of N₂O₃?

What you need to do here is determine first how many moles of that atom we have in mole of the compound. Remember, this we are doing based on the chemical formula. Every 1 mole of N₂O₃contains 2 moles of N because every molecule of N₂O₃contains 2 atoms of nitrogen. Therefore, once we calculate the moles of the oxide, we can multiply it by 2 to determine the moles of the nitrogen.

\[{\rm{n}}\,{\rm{(}}{{\rm{N}}_{\rm{2}}}{{\rm{O}}_{\rm{3}}}{\rm{)}}\;{\rm{ = }}\,{\rm{46}}{\rm{.0}}\,\cancel{{{\rm{g}}\,{{\rm{N}}_{\rm{2}}}{{\rm{O}}_{\rm{3}}}}}{\rm{ \times }}\,\frac{{{\rm{1}}\;{\rm{mol}}\;{{\rm{N}}_{\rm{2}}}{{\rm{O}}_{\rm{3}}}}}{{{\rm{76}}{\rm{.01}}\;\cancel{{{\rm{g}}\,{{\rm{N}}_{\rm{2}}}{{\rm{O}}_{\rm{3}}}}}}}\,{\rm{ = }}\,{\rm{0}}{\rm{.605}}\;{\rm{mol}}\,{{\rm{N}}_{\rm{2}}}{{\rm{O}}_{\rm{3}}}\]

Next, we multiply this by 2:

n (N) = 2 n (N₂O₃) = 2 x 0.605 mol = 1.21 mol

We can also do this calculation in one step using conversion factors:

\[{\rm{n}}\,{\rm{(N)}}\;{\rm{ = }}\,{\rm{46}}{\rm{.0}}\,\cancel{{{\rm{g}}\,{{\rm{N}}_{\rm{2}}}{{\rm{O}}_{\rm{3}}}}}{\rm{ \times }}\,\frac{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{{\rm{N}}_{\rm{2}}}{{\rm{O}}_{\rm{3}}}}}}}{{{\rm{76}}{\rm{.01}}\;\cancel{{{\rm{g}}\,{{\rm{N}}_{\rm{2}}}{{\rm{O}}_{\rm{3}}}}}}}\,{\rm{ \times }}\,\frac{{{\rm{2}}\;{\rm{mol}}\;{\rm{N}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{{\rm{N}}_{\rm{2}}}{{\rm{O}}_{\rm{3}}}}}}}{\rm{ = }}\,{\rm{1}}{\rm{.21}}\;{\rm{mol}}\,{\rm{N}}\]

Converting Moles to Mass

If the question asks to calculate the mass from the moles, we will need to use the other conversion factor so that the moles now can be canceled.

For example, how many moles of carbon are there in a 0.048 mol sample?

The molar mass of carbon is 12.0 g/mol, so the conversion factors are:

\[\frac{{{\rm{1}}\;{\rm{mol}}\;{\rm{C}}}}{{{\rm{12}}{\rm{.0}}\;{\rm{g}}\,{\rm{S}}}}\;\,and\,\,\frac{{{\rm{12}}{\rm{.0}}\;{\rm{g}}\,{\rm{C}}}}{{{\rm{1}}\;{\rm{mol}}\;{\rm{C}}}}\]

Using the second conversion factor, we can calculate the mass as:

\[{\rm{m}}\;{\rm{(C)}}\,{\rm{ = }}\;{\rm{0}}{\rm{.048}}\;\cancel{{{\rm{mol}}\,{\rm{C}}}}\,{\rm{ \times }}\,\frac{{{\rm{12}}{\rm{.0}}\;{\rm{g}}\,{\rm{C}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{C}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.576}}\,{\rm{g}}\]

Practice

Calculating Moles from Mass

Determine the number of moles in 59.7 grams of Al.

answer

2.21 mol

Solution

The moles and mass are connected through the molar mass. The molar mass of Al is 27.0 g/mol, therefore the conversion factor is:

\[\frac{{{\rm{27}}{\rm{.0}}\;{\rm{g}}\,{\rm{Al}}}}{{{\rm{1}}\;{\rm{mol}}}}\]

\[{\rm{n}}\;{\rm{(Al)}}\,{\rm{ = }}\;{\rm{59}}{\rm{.7}}\cancel{{{\rm{g}}\,{\rm{Al}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{mol}}}}{{{\rm{27}}{\rm{.0}}\,\cancel{{{\rm{g}}\,{\rm{Al}}}}}}\;{\rm{ = }}\;{\rm{2}}{\rm{.21}}\;{\rm{mol}}\]

Determine the number of moles in 2.41 grams of FeO.

answer

0.0336 mol

Solution

The moles and mass are connected through the molar mass. The molar mass of FeO is 71.8 g/mol, therefore the conversion factor is:

\[\frac{{{\rm{71}}{\rm{.8}}\;{\rm{g}}\,{\rm{FeO}}}}{{{\rm{1}}\;{\rm{mol}}}}\]

\[{\rm{n}}\;{\rm{(FeO)}}\,{\rm{ = }}\;{\rm{2}}{\rm{.41}}\cancel{{{\rm{g}}\,{\rm{FeO}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{mol}}}}{{{\rm{71}}{\rm{.8}}\,\cancel{{{\rm{g}}\,{\rm{FeO}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.0336}}\;{\rm{mol}}\]

Calculate the number of moles in 0.647 grams of Al₂O₃.

answer

0.00634 mol

Solution

The moles and mass are connected through the molar mass. The molar mass of Al₂O₃ is 102 g/mol, therefore the conversion factor is:

\[\frac{{{\rm{102}}\;{\rm{g}}\,{\rm{A}}{{\rm{l}}_{\rm{2}}}{{\rm{O}}_{\rm{3}}}}}{{{\rm{1}}\;{\rm{mol}}}}\]

\[{\rm{n}}\;{\rm{(A}}{{\rm{l}}_{\rm{2}}}{{\rm{O}}_{\rm{3}}}{\rm{)}}\,{\rm{ = }}\;{\rm{0}}{\rm{.647}}\cancel{{{\rm{g}}\,{\rm{A}}{{\rm{l}}_{\rm{2}}}{{\rm{O}}_{\rm{3}}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{mol}}}}{{{\rm{102}}\,\cancel{{{\rm{g}}\,{\rm{A}}{{\rm{l}}_{\rm{2}}}{{\rm{O}}_{\rm{3}}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.00634}}\;{\rm{mol}}\]

Determine the number of moles in 3.56 grams of Mg(OH)₂.

answer

0.0611 mol

Solution

The moles and mass are connected through the molar mass. The molar mass of Mg(OH)₂ is 58.3 g/mol, therefore the conversion factor is:

\[\frac{{{\rm{58}}{\rm{.3}}\;{\rm{g}}\,{\rm{Mg}}{{\left( {{\rm{OH}}} \right)}_{\rm{2}}}}}{{{\rm{1}}\;{\rm{mol}}}}\]

\[{\rm{n}}\;{\rm{(Mg}}{\left( {{\rm{OH}}} \right)_{\rm{2}}}{\rm{)}}\,{\rm{ = }}\;{\rm{3}}{\rm{.56}}\cancel{{{\rm{g}}\,{\rm{Mg}}{{\left( {{\rm{OH}}} \right)}_{\rm{2}}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{mol}}}}{{{\rm{58}}{\rm{.3}}\,\cancel{{{\rm{g}}\,{\rm{Mg}}{{\left( {{\rm{OH}}} \right)}_{\rm{2}}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.0611}}\;{\rm{mol}}\]

Determine the number of moles in 0.385 grams of N₂O₃.

answer

0.00507 mol

Solution

The moles and mass are connected through the molar mass. The molar mass of N₂O₃ is 76.0 g/mol, therefore the conversion factor is:

\[\frac{{{\rm{76}}{\rm{.0}}\;{\rm{g}}\,{{\rm{N}}_{\rm{2}}}{{\rm{O}}_{\rm{3}}}}}{{{\rm{1}}\;{\rm{mol}}}}\]

\[{\rm{n}}\;{\rm{(}}{{\rm{N}}_{\rm{2}}}{{\rm{O}}_{\rm{3}}}{\rm{)}}\,{\rm{ = }}\;{\rm{0}}{\rm{.385}}\cancel{{{\rm{g}}\,{{\rm{N}}_{\rm{2}}}{{\rm{O}}_{\rm{3}}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{mol}}}}{{{\rm{76}}{\rm{.0}}\,\cancel{{{\rm{g}}\,{{\rm{N}}_{\rm{2}}}{{\rm{O}}_{\rm{3}}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.00507}}\;{\rm{mol}}\]

Determine the number of moles in 165 grams of CaSO₄.

answer

1.21 mol

Solution

The moles and mass are connected through the molar mass. The molar mass of CaSO₄ is 136.1 g/mol, therefore the conversion factor is:

\[\frac{{{\rm{136}}{\rm{.1}}\;{\rm{g}}\,{\rm{CaS}}{{\rm{O}}_{\rm{4}}}}}{{{\rm{1}}\;{\rm{mol}}}}\]

\[{\rm{n}}\;{\rm{(CaS}}{{\rm{O}}_{\rm{4}}}{\rm{)}}\,{\rm{ = }}\;{\rm{165}}\cancel{{{\rm{g}}\,{\rm{CaS}}{{\rm{O}}_{\rm{4}}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{mol}}}}{{{\rm{136}}{\rm{.1}}\,\cancel{{{\rm{g}}\,{\rm{CaS}}{{\rm{O}}_{\rm{4}}}}}}}\;{\rm{ = }}\;{\rm{1}}{\rm{.21}}\;{\rm{mol}}\]

Calculate the molar mass of N₂O₄ and determine how many moles of it are in a 23.9 g sample.

answer

0.260 mol

Solution

The moles and mass are connected through the molar mass. The molar mass of N₂O₄ is 92.0 g/mol, therefore the conversion factor is:

\[\frac{{{\rm{92}}{\rm{.0}}\;{\rm{g}}\,{{\rm{N}}_{\rm{2}}}{{\rm{O}}_{\rm{4}}}}}{{{\rm{1}}\;{\rm{mol}}}}\]

\[{\rm{n}}\;{\rm{(}}{{\rm{N}}_{\rm{2}}}{{\rm{O}}_{\rm{4}}}{\rm{)}}\,{\rm{ = }}\;{\rm{23}}{\rm{.9}}\cancel{{{\rm{g}}\,{{\rm{N}}_{\rm{2}}}{{\rm{O}}_{\rm{4}}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{mol}}}}{{{\rm{92}}{\rm{.0}}\,\cancel{{{\rm{g}}\,{{\rm{N}}_{\rm{2}}}{{\rm{O}}_{\rm{4}}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.260}}\;{\rm{mol}}\]

Calculate the number of moles in 165 grams of C₃H₆O.

answer

2.84 mol

Solution

The moles and mass are connected through the molar mass. The molar mass of C₃H₆O is 58.1 g/mol, therefore the conversion factor is:

\[\frac{{{\rm{58}}{\rm{.1}}\;{\rm{g}}\,{{\rm{C}}_{\rm{3}}}{{\rm{H}}_{\rm{6}}}{\rm{O}}}}{{{\rm{1}}\;{\rm{mol}}}}\]

\[{\rm{n}}\;{\rm{(}}{{\rm{C}}_{\rm{3}}}{{\rm{H}}_{\rm{6}}}{\rm{O)}}\,{\rm{ = }}\;{\rm{165}}\cancel{{{\rm{g}}\,{{\rm{C}}_{\rm{3}}}{{\rm{H}}_{\rm{6}}}{\rm{O}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{mol}}}}{{{\rm{58}}{\rm{.1}}\,\cancel{{{\rm{g}}\,{{\rm{C}}_{\rm{3}}}{{\rm{H}}_{\rm{6}}}{\rm{O}}}}}}\;{\rm{ = }}\;{\rm{2}}{\rm{.84}}\;{\rm{mol}}\]

Determine the number of moles in 452 grams of Co(NO₃)₃.

answer

1.84 mol

Solution

The moles and mass are connected through the molar mass. The molar mass of Co(NO₃)₃ is 245 g/mol, therefore the conversion factor is:

\[\frac{{{\rm{245}}\;{\rm{g}}\,{\rm{Co}}{{\left( {{\rm{N}}{{\rm{O}}_{\rm{3}}}} \right)}_{\rm{3}}}}}{{{\rm{1}}\;{\rm{mol}}}}\]

\[{\rm{n}}\;{\rm{(Co}}{\left( {{\rm{N}}{{\rm{O}}_{\rm{3}}}} \right)_{\rm{3}}}{\rm{)}}\,{\rm{ = }}\;{\rm{452}}\cancel{{{\rm{g}}\,{\rm{Co}}{{\left( {{\rm{N}}{{\rm{O}}_{\rm{3}}}} \right)}_{\rm{3}}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{mol}}}}{{{\rm{245}}\,\cancel{{{\rm{g}}\,{\rm{Co}}{{\left( {{\rm{N}}{{\rm{O}}_{\rm{3}}}} \right)}_{\rm{3}}}}}}}\;{\rm{ = }}\;{\rm{1}}{\rm{.84}}\;{\rm{mol}}\]

10.

Calculating Mass from Moles

Calculate the mass in grams of 0.598 moles of Fe.

answer

33.4 g

Solution

The molar mass of Fe is 55.8 g/mol, therefore the conversion factor is:

\[\frac{{{\rm{55}}{\rm{.8}}\;{\rm{g}}\,{\rm{Fe}}}}{{{\rm{1}}\;{\rm{mol}}}}\]

\[{\rm{m}}\;{\rm{(Fe)}}\,{\rm{ = }}\;{\rm{0}}{\rm{.598}}\;\cancel{{{\rm{mol}}\,{\rm{Fe}}}}\,{\rm{ \times }}\,\frac{{{\rm{55}}{\rm{.8}}\;{\rm{g}}\,{\rm{Fe}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{Fe}}}}}}\;{\rm{ = }}\;{\rm{33}}{\rm{.4}}\;{\rm{g}}\]

11.

Calculate the mass in grams of 0.168 moles of NO.

answer

5.04 g

Solution

The molar mass of NO is 30.0 g/mol, therefore the conversion factor is:

\[\frac{{{\rm{30}}{\rm{.0}}\;{\rm{g}}\,{\rm{NO}}}}{{{\rm{1}}\;{\rm{mol}}}}\]

\[{\rm{m}}\;{\rm{(NO)}}\,{\rm{ = }}\;{\rm{0}}{\rm{.168}}\;\cancel{{{\rm{mol}}\,{\rm{NO}}}}\,{\rm{ \times }}\,\frac{{{\rm{30}}{\rm{.0}}\;{\rm{g}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{NO}}}}}}\;{\rm{ = }}\;{\rm{5}}{\rm{.04}}\;{\rm{g}}\]

12.

Calculate the mass in grams of 0.987 moles of (NH₄)₂S.

answer

67.3 g

Solution

The molar mass of (NH₄)₂S is 68.2 g/mol, therefore the conversion factor is:

\[\frac{{{\rm{68}}{\rm{.2}}\;{\rm{g}}\,{{\left( {{\rm{N}}{{\rm{H}}_{\rm{4}}}} \right)}_{\rm{2}}}{\rm{S}}}}{{{\rm{1}}\;{\rm{mol}}}}\]

\[{\rm{m}}\;{\rm{(}}{\left( {{\rm{N}}{{\rm{H}}_{\rm{4}}}} \right)_{\rm{2}}}{\rm{S)}}\,{\rm{ = }}\;{\rm{0}}{\rm{.987}}\;\cancel{{{\rm{mol}}\,{{\left( {{\rm{N}}{{\rm{H}}_{\rm{4}}}} \right)}_{\rm{2}}}{\rm{S}}}}\,{\rm{ \times }}\,\frac{{{\rm{68}}{\rm{.2}}\;{\rm{g}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{{\left( {{\rm{N}}{{\rm{H}}_{\rm{4}}}} \right)}_{\rm{2}}}{\rm{S}}}}}}\;{\rm{ = }}\;{\rm{67}}{\rm{.3}}\;{\rm{g}}\]

13.

Calculate the mass in grams of 6.81 moles of Al₂(SO₄)₃.

answer

2.33 x 10³ g

Solution

The molar mass of Al₂(SO₄)₃is 342.2 g/mol, therefore the conversion factor is:

\[\frac{{{\rm{342}}{\rm{.2}}\;{\rm{g}}\,{\rm{A}}{{\rm{l}}_{\rm{2}}}{{\left( {{\rm{S}}{{\rm{O}}_{\rm{4}}}} \right)}_{\rm{3}}}}}{{{\rm{1}}\;{\rm{mol}}}}\]

\[{\rm{m}}\;{\rm{(A}}{{\rm{l}}_{\rm{2}}}{\left( {{\rm{S}}{{\rm{O}}_{\rm{4}}}} \right)_{\rm{3}}}{\rm{)}}\,{\rm{ = }}\;{\rm{6}}{\rm{.81}}\;\cancel{{{\rm{mol}}\,{\rm{A}}{{\rm{l}}_{\rm{2}}}{{\left( {{\rm{S}}{{\rm{O}}_{\rm{4}}}} \right)}_{\rm{3}}}}}\,{\rm{ \times }}\,\frac{{{\rm{342}}{\rm{.2}}\;{\rm{g}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{A}}{{\rm{l}}_{\rm{2}}}{{\left( {{\rm{S}}{{\rm{O}}_{\rm{4}}}} \right)}_{\rm{3}}}}}}}\;{\rm{ = }}\;{\rm{2}}{\rm{.33}}\, \times \;{10^3}\;{\rm{g}}\]

14.

Calculate the mass in grams of 2.64 moles of methanol, CH₃OH.

answer

84.5 g

Solution

The molar mass of CH₃OH is 32.0 g/mol, therefore the conversion factor is:

\[\frac{{{\rm{32}}{\rm{.0}}\;{\rm{g}}\,{\rm{C}}{{\rm{H}}_{\rm{3}}}{\rm{OH}}}}{{{\rm{1}}\;{\rm{mol}}}}\]

\[{\rm{m}}\;{\rm{(C}}{{\rm{H}}_{\rm{3}}}{\rm{OH)}}\,{\rm{ = }}\;{\rm{2}}{\rm{.64}}\;\cancel{{{\rm{mol}}\,{\rm{C}}{{\rm{H}}_{\rm{3}}}{\rm{OH}}}}\,{\rm{ \times }}\,\frac{{{\rm{32}}{\rm{.0}}\;{\rm{g}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{C}}{{\rm{H}}_{\rm{3}}}{\rm{OH}}}}}}\;{\rm{ = }}\;{\rm{84}}{\rm{.5}}\;{\rm{g}}\]

15.

Calculate the mass in grams of 9.42 moles of NiCl₂·6H₂O.

answer

2.24 x 10³ g

Solution

The molar mass of NiCl₂·6H₂O is 129.6 g/mol. Do not forget to add the mass of 6 moles of H₂O (6 x 18 = 108 g/mol) to the molar mass of NiCl_2. Therefore, the conversion factor is:

\[\frac{{{\rm{237}}{\rm{.6}}\;{\rm{g}}\,{\rm{NiC}}{{\rm{l}}_{\rm{2}}}{\rm{\cdot6}}{{\rm{H}}_{\rm{2}}}{\rm{O}}}}{{{\rm{1}}\;{\rm{mol}}}}\]

\[{\rm{m}}\;{\rm{(NiC}}{{\rm{l}}_{\rm{2}}}{\rm{\cdot6}}{{\rm{H}}_{\rm{2}}}{\rm{O)}}\,{\rm{ = }}\;{\rm{9}}{\rm{.42}}\;\cancel{{{\rm{mol}}\,{\rm{NiC}}{{\rm{l}}_{\rm{2}}}{\rm{\cdot6}}{{\rm{H}}_{\rm{2}}}{\rm{O}}}}\,{\rm{ \times }}\,\frac{{{\rm{237}}{\rm{.6}}\;{\rm{g}}}}{{{\rm{1}}\;\cancel{{{\rm{mol}}\;{\rm{NiC}}{{\rm{l}}_{\rm{2}}}{\rm{\cdot6}}{{\rm{H}}_{\rm{2}}}{\rm{O}}}}}}\;{\rm{ = }}\;{\rm{2}}{\rm{.24}}\, \times \,{\rm{1}}{{\rm{0}}^{\rm{3}}}\;{\rm{g}}\]

16.

Calculating the Number of Molecules from the Moles

How many molecules are there in a 0.487 mol sample of PCl₅?

answer

2.93 x 10²³

Solution

To determine the number of molecules, we use the Avogadro’s number which shows the number of particles (molecules) in one mole of the sample.

\[\frac{{{\rm{6}}{\rm{.02}}\;{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{23}}}}\;{\rm{molecules}}}}{{{\rm{1}}\,{\rm{mol}}}}\,\,or\,\,\frac{{{\rm{1}}\,{\rm{mol}}}}{{{\rm{6}}{\rm{.02}}\;{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{23}}}}\;{\rm{molecules}}}}\;\;\;\;\]

\[{\rm{N}}\;{\rm{(PC}}{{\rm{l}}_{\rm{5}}}{\rm{)}}\,{\rm{ = }}\;{\rm{0}}{\rm{.487}}\,\cancel{{{\rm{mol}}\,{\rm{PC}}{{\rm{l}}_{\rm{5}}}}}\;{\rm{ \times }}\,\frac{{{\rm{6}}{\rm{.022}}\;{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{23}}}}\;{\rm{PC}}{{\rm{l}}_{\rm{5}}}\,{\rm{molecules}}}}{{{\rm{1}}\,\cancel{{{\rm{mol}}\,{\rm{PC}}{{\rm{l}}_{\rm{5}}}}}}}\; = \;2.93\;{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{23}}}}\;\;\;\]

17.

How many molecules (formula units) are there in a 5.84 mol sample of Na₂SO₃.

answer

3.52 x 10²⁴

Solution

\[{\rm{N}}\;{\rm{(N}}{{\rm{a}}_{\rm{2}}}{\rm{S}}{{\rm{O}}_{\rm{3}}}{\rm{)}}\,{\rm{ = }}\;{\rm{5}}{\rm{.84}}\,\cancel{{{\rm{mol}}\,{\rm{N}}{{\rm{a}}_{\rm{2}}}{\rm{S}}{{\rm{O}}_{\rm{3}}}}}\;{\rm{ \times }}\,\frac{{{\rm{6}}{\rm{.022}}\;{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{23}}}}\;{\rm{N}}{{\rm{a}}_{\rm{2}}}{\rm{S}}{{\rm{O}}_{\rm{3}}}\,{\rm{molecules}}}}{{{\rm{1}}\,\cancel{{{\rm{mol}}\,{\rm{N}}{{\rm{a}}_{\rm{2}}}{\rm{S}}{{\rm{O}}_{\rm{3}}}}}}}\; = \;3.52\;{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{24}}}}\;\;\;\]

18.

How many molecules of sucrose, C₁₂H₂₂O₁₁ are there in a 0.684 mol sample?

answer

4.12 x 10²³

Solution

\[{\rm{N}}\;{\rm{(}}{{\rm{C}}_{{\rm{12}}}}{{\rm{H}}_{{\rm{22}}}}{{\rm{O}}_{{\rm{11}}}}{\rm{)}}\,{\rm{ = }}\;{\rm{0}}{\rm{.684}}\,\cancel{{{\rm{mol}}\,{{\rm{C}}_{{\rm{12}}}}{{\rm{H}}_{{\rm{22}}}}{{\rm{O}}_{{\rm{11}}}}}}\;{\rm{ \times }}\,\frac{{{\rm{6}}{\rm{.022}}\;{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{23}}}}\;{{\rm{C}}_{{\rm{12}}}}{{\rm{H}}_{{\rm{22}}}}{{\rm{O}}_{{\rm{11}}}}\,{\rm{molecules}}}}{{{\rm{1}}\,\cancel{{{\rm{mol}}\,{{\rm{C}}_{{\rm{12}}}}{{\rm{H}}_{{\rm{22}}}}{{\rm{O}}_{{\rm{11}}}}}}}}\; = \;4.12\;{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{23}}}}\;\;\;\]

19.

Calculate the number of molecules in a 3.25-mol sample of propane, C₃H₈.

answer

1.96 x 10²⁴

Solution

\[{\rm{N}}\;{\rm{(}}{{\rm{C}}_{\rm{3}}}{{\rm{H}}_{\rm{8}}}{\rm{)}}\,{\rm{ = }}\;{\rm{3}}{\rm{.25}}\,\cancel{{{\rm{mol}}\,{{\rm{C}}_{\rm{3}}}{{\rm{H}}_{\rm{8}}}}}\;{\rm{ \times }}\,\frac{{{\rm{6}}{\rm{.022}}\;{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{23}}}}\;{{\rm{C}}_{\rm{3}}}{{\rm{H}}_{\rm{8}}}\,{\rm{molecules}}}}{{{\rm{1}}\,\cancel{{{\rm{mol}}\,{{\rm{C}}_{\rm{3}}}{{\rm{H}}_{\rm{8}}}}}}}\; = \;1.96\;{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{24}}}}\;\;\;\]

20.

How many moles is 5.80 x 10²⁵ molecules of POCl₃?

answer

96.3 moles

Solution

This is a conversion in reverse directions, therefore, we use the other conversion factor linking the number of moles and number of molecules.

\[{\rm{n}}\;{\rm{(POC}}{{\rm{l}}_{\rm{3}}}{\rm{)}}\,{\rm{ = }}\;5.80\; \times \;{10^{25}}\,\cancel{{{\rm{molecules}}\,{\rm{POC}}{{\rm{l}}_{\rm{3}}}\,}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{mol}}\,{\rm{POC}}{{\rm{l}}_{\rm{3}}}{\rm{ }}}}{{{\rm{6}}{\rm{.022}}\;{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{23}}}}\,\cancel{{{\rm{molecules}}\;{\rm{POC}}{{\rm{l}}_{\rm{3}}}}}}}\; = \;96.3\,{\rm{moles}}\;\;\;\]

21.

Calculating the Number of Molecules from the Mass

How many molecules are there in a 5.12-g sample of K₂O?

answer

3.27 x 10²²

Solution

There is an extra step here which is to first convert the mass to moles. After this, it is the same conversion as we have seen in the previous section for converting moles to the number of molecules using the Avogadro’s number. You can solve these types of problems by step-by-step or one-step conversion.

The first step is to convert the mass to moles:

\[{\rm{n}}\;{\rm{(}}{{\rm{K}}_{\rm{2}}}{\rm{O)}}\,{\rm{ = }}\;{\rm{5}}{\rm{.12}}\cancel{{\rm{g}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\cancel{{{\rm{mol}}}}{{\rm{K}}_{\rm{2}}}{\rm{O}}}}{{{\rm{94}}{\rm{.2}}\cancel{{\rm{g}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.0543524}}\;{\rm{mol}}\;\]

Keep the decimals and round them off in the last step.

Once we have the number of moles, we can calculate the number of molecules.

\[{\rm{N}}\;{\rm{(}}{{\rm{K}}_{\rm{2}}}{\rm{O)}}\,{\rm{ = }}\;{\rm{0}}{\rm{.0543524}}\,\cancel{{{\rm{mol}}\,{{\rm{K}}_{\rm{2}}}{\rm{O}}}}\;{\rm{ \times }}\,\frac{{{\rm{6}}{\rm{.022}}\;{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{23}}}}\;{{\rm{K}}_{\rm{2}}}{\rm{O}}\,{\rm{molecules}}}}{{{\rm{1}}\,\cancel{{{\rm{mol}}\,{{\rm{K}}_{\rm{2}}}{\rm{O}}}}}}\; = \;3.27\;{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{22}}}}\;\;\;\]

A quicker method is to combine these two steps in one. Just make sure to use the correct conversion factor that allows canceling the units.

\[{\rm{N}}\;{\rm{(}}{{\rm{K}}_{\rm{2}}}{\rm{O)}}\,{\rm{ = }}\;{\rm{5}}{\rm{.12}}\cancel{{\rm{g}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\cancel{{{\rm{mol}}\,{{\rm{K}}_{\rm{2}}}{\rm{O}}}}}}{{{\rm{94}}{\rm{.2}}\cancel{{\rm{g}}}}}\;{\rm{ \times }}\,\frac{{{\rm{6}}{\rm{.022}}\;{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{23}}}}\;{{\rm{K}}_{\rm{2}}}{\rm{O}}\,{\rm{molecules}}}}{{{\rm{1}}\,\cancel{{{\rm{mol}}\,{{\rm{K}}_{\rm{2}}}{\rm{O}}}}}}\; = \;3.27\;{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{22}}}}\;\;\;\]

22.

How many molecules of glucose, C₆H₁₂O₆ are there in a 35.0 g sample?

answer

1.17 x 10²³

Solution

Refer to the first problem in “Calculating the number of molecules from the mass” for a detailed explanation.

\[{\rm{N}}\;{\rm{(}}{{\rm{C}}_{\rm{6}}}{{\rm{H}}_{{\rm{12}}}}{{\rm{O}}_{\rm{6}}}{\rm{)}}\,{\rm{ = }}\;{\rm{35}}{\rm{.0}}\cancel{{\rm{g}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\cancel{{{\rm{mol}}\,{{\rm{C}}_{\rm{6}}}{{\rm{H}}_{{\rm{12}}}}{{\rm{O}}_{\rm{6}}}}}}}{{{\rm{180}}{\rm{.2}}\cancel{{\rm{g}}}}}\;{\rm{ \times }}\,\frac{{{\rm{6}}{\rm{.022}}\;{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{23}}}}\;{{\rm{C}}_{\rm{6}}}{{\rm{H}}_{{\rm{12}}}}{{\rm{O}}_{\rm{6}}}\,{\rm{molecules}}}}{{{\rm{1}}\,\cancel{{{\rm{mol}}\,{{\rm{C}}_{\rm{6}}}{{\rm{H}}_{{\rm{12}}}}{{\rm{O}}_{\rm{6}}}}}}}\; = \;1.17\;{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{23}}}}\;\;\;\]

23.

Calculate the number of molecules of butane, C₄H₁₀, in its 2.40-gram sample.

answer

2.49 x 10²²

Solution

\[{\rm{N}}\;{\rm{(}}{{\rm{C}}_{\rm{4}}}{{\rm{H}}_{{\rm{10}}}}{\rm{)}}\,{\rm{ = }}\;{\rm{2}}{\rm{.40}}\cancel{{\rm{g}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\cancel{{{\rm{mol}}\,{{\rm{C}}_{\rm{4}}}{{\rm{H}}_{{\rm{10}}}}}}}}{{{\rm{58}}{\rm{.1}}\cancel{{\rm{g}}}}}\;{\rm{ \times }}\,\frac{{{\rm{6}}{\rm{.022}}\;{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{23}}}}\;{{\rm{C}}_{\rm{4}}}{{\rm{H}}_{{\rm{10}}}}\,{\rm{molecules}}}}{{{\rm{1}}\,\cancel{{{\rm{mol}}\,{{\rm{C}}_{\rm{4}}}{{\rm{H}}_{{\rm{10}}}}}}}}\; = \;2.49\;{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{22}}}}\;\;\;\]

24.

How many Ethylene, C₂H₄ molecules are present in a 46.2 g sample? The molar mass of C₂H₄ is 28.1 g/mol.

answer

9.90 x 10²³

Solution

\[{\rm{N}}\;{\rm{(}}{{\rm{C}}_{\rm{2}}}{{\rm{H}}_{\rm{4}}}{\rm{)}}\,{\rm{ = }}\;{\rm{46}}{\rm{.2}}\cancel{{\rm{g}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\cancel{{{\rm{mol}}\,{{\rm{C}}_{\rm{2}}}{{\rm{H}}_{\rm{4}}}}}}}{{{\rm{28}}{\rm{.1}}\cancel{{\rm{g}}}}}\;{\rm{ \times }}\,\frac{{{\rm{6}}{\rm{.022}}\;{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{23}}}}\;{{\rm{C}}_{\rm{2}}}{{\rm{H}}_{\rm{4}}}\,{\rm{molecules}}}}{{{\rm{1}}\,\cancel{{{\rm{mol}}\,{{\rm{C}}_{\rm{2}}}{{\rm{H}}_{\rm{4}}}}}}}\; = \;9.90\;{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{23}}}}\;\;\;\]

25.

Calculating the Number of Atoms

Calculate the number of atoms in a 2.56-g sample of Ca.

answer

3.84 x 10²²

Solution

We have seen how to convert the number of moles to the number of molecules using the Avogadros’ number. Finding the number of atoms follows the same steps when working with atoms. Because one mole contains 6.022 x 10²³ atoms of Ca, we can calculate the number of atoms by multiplying the number of moles by the Avogadro’s number:

\[{\rm{N}}\;{\rm{(Ca)}}\,{\rm{ = }}\;{\rm{2}}{\rm{.56}}\cancel{{\rm{g}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\cancel{{{\rm{mol}}\,{\rm{Ca}}}}}}{{{\rm{40}}{\rm{.1}}\cancel{{\rm{g}}}}}\;{\rm{ \times }}\,\frac{{{\rm{6}}{\rm{.022}}\;{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{23}}}}\;{\rm{Ca}}\,{\rm{atoms}}}}{{{\rm{1}}\,\cancel{{{\rm{mol}}\,{\rm{Ca}}}}}}\; = \;3.84\;{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{22}}}}\;\;\;\]

26.

How many carbon atoms are there in a 0.590 mol sample of CCl₄.

answer

3.55 x 10²³

Solution

To find the number of atoms/ions in a molecule, multiply the number of molecules by the subscript of that atom. In this case, the subscript of carbon is one, so the number of carbon atoms is going to be equal to the number of molecules.

\[{\rm{N}}\;{\rm{(C atoms)}}\,{\rm{ = }}\;{\rm{0}}{\rm{.590}}\,\cancel{{{\rm{mol}}\,{\rm{CC}}{{\rm{l}}_{\rm{4}}}}}\;{\rm{ \times }}\,\frac{{{\rm{6}}{\rm{.022}}\;{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{23}}}}\;\cancel{{{\rm{CC}}{{\rm{l}}_{\rm{4}}}\,{\rm{molecules}}}}}}{{{\rm{1}}\,\cancel{{{\rm{mol}}\,{\rm{CC}}{{\rm{l}}_{\rm{4}}}}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{atom}}\,{\rm{of}}\,{\rm{C}}}}{{{\rm{1}}\,\cancel{{{\rm{CC}}{{\rm{l}}_{\rm{4}}}\,{\rm{molecule}}}}\,}}\; = \;3.55\;{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{23}}}}\;\;\;\]

27.

How many carbon atoms are there in a 0.964 mol sample of C₂H₆.

answer

1.16 x 10²⁴

Solution

This is very similar to the previous example with the difference that there are 2 carbon atoms in each molecule of C₂H_6.Therefore, there is going to be twice more carbon atoms than C2H6 molecules.

\[{\rm{N}}\;{\rm{(C atoms)}}\,{\rm{ = }}\;{\rm{0}}{\rm{.964}}\,\cancel{{{\rm{mol}}\,{{\rm{C}}_{\rm{2}}}{{\rm{H}}_{\rm{6}}}}}\;{\rm{ \times }}\,\frac{{{\rm{6}}{\rm{.022}}\;{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{23}}}}\;\cancel{{{{\rm{C}}_{\rm{2}}}{{\rm{H}}_{\rm{6}}}\,{\rm{molecules}}}}}}{{{\rm{1}}\,\cancel{{{\rm{mol}}\,{{\rm{C}}_{\rm{2}}}{{\rm{H}}_{\rm{6}}}}}}}\;{\rm{ \times }}\,\frac{{{\rm{2}}\,{\rm{atom}}\,{\rm{of}}\,{\rm{C}}}}{{{\rm{1}}\,\cancel{{{{\rm{C}}_{\rm{2}}}{{\rm{H}}_{\rm{6}}}\,{\rm{molecule}}}}\,}}\; = \;1.16\;{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{24}}}}\;\;\;\]

So, if we stop the conversion before the last step, we’d see that there are 5.805 x 10²³ molecules of C₂H₆ and therefore, we multiply that number by two to determine the number of carbon atoms.

28.

Which sample contains more Cl atoms: a) 1.25 moles of CH₂Cl₂ b) 2.15 moles of CH₃Cl

answer

a) 1.25 moles of CH₂Cl₂

Solution

Sometimes, you may need to save time and solve the problem using a shortcut. For example, here, if we figure out which sample has a greater number of moles of Cl, we can conclude that it also has more Cl atoms because we only multiply both numbers by the Avogadros’ number.

So, 1.25 mol CH₂Cl₂contains 2 x 1.25 = 2.50 mol Cl atoms. 2.15 mol CH₃Cl, on the other hand, contains the same number of Cl atoms because each molecule contains one atom of Cl.

Therefore, 1.25 mol CH₂Cl₂contains more Cl atoms than 2.15 mol CH₃Cl.

Let’s confirm this with a complete calculation to practice it a little more too:

\[{\rm{N}}\;{\rm{(Cl atoms)}}\,{\rm{ = }}\;{\rm{1}}{\rm{.25}}\,\cancel{{{\rm{mol}}\,{\rm{C}}{{\rm{H}}_{\rm{2}}}{\rm{C}}{{\rm{l}}_{\rm{2}}}}}\;{\rm{ \times }}\,\frac{{{\rm{6}}{\rm{.022}}\;{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{23}}}}\;\cancel{{{\rm{C}}{{\rm{H}}_{\rm{2}}}{\rm{C}}{{\rm{l}}_{\rm{2}}}\,{\rm{molecules}}}}}}{{{\rm{1}}\,\cancel{{{\rm{mol}}\,{\rm{C}}{{\rm{H}}_{\rm{2}}}{\rm{C}}{{\rm{l}}_{\rm{2}}}}}}}\;{\rm{ \times }}\,\frac{{{\rm{2}}\,{\rm{atom}}\,{\rm{of}}\,{\rm{Cl}}}}{{{\rm{1}}\,\cancel{{{\rm{C}}{{\rm{H}}_{\rm{2}}}{\rm{C}}{{\rm{l}}_{\rm{2}}}\,{\rm{molecule}}}}\,}}\; = \;1.51\;{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{24}}}}\;\;\;\]

\[{\rm{N}}\;{\rm{(Cl atoms)}}\,{\rm{ = }}\;{\rm{2}}{\rm{.15}}\,\cancel{{{\rm{mol}}\,{\rm{C}}{{\rm{H}}_{\rm{3}}}{\rm{Cl}}}}\;{\rm{ \times }}\,\frac{{{\rm{6}}{\rm{.022}}\;{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{23}}}}\;\cancel{{{\rm{C}}{{\rm{H}}_{\rm{3}}}{\rm{Cl}}\,{\rm{molecules}}}}}}{{{\rm{1}}\,\cancel{{{\rm{mol}}\,{\rm{C}}{{\rm{H}}_{\rm{3}}}{\rm{Cl}}}}}}\;{\rm{ \times }}\,\frac{{{\rm{1}}\,{\rm{atom}}\,{\rm{of}}\,{\rm{Cl}}}}{{{\rm{1}}\,\cancel{{{\rm{C}}{{\rm{H}}_{\rm{3}}}{\rm{Cl}}\,{\rm{molecule}}}}\,}}\; = \;1.29\;{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{24}}}}\;\;\;\]

29.

The molecular formula of morphine is C₁₇H₁₉NO₃. How many carbon atoms are in a 34.7-gram sample of morphine?

answer

1.25 x 10²⁴

Solution

One molecule of C₁₇H₁₉NO₃contains 17 carbon atoms, so once we find the number of molecules, we multiply it by 17:

\[{\rm{N}}\;{\rm{(C}}\,{\rm{atoms)}}\,{\rm{ = }}\;{\rm{34}}{\rm{.7}}\;\cancel{{{\rm{g}}\;{\rm{Mor}}{\rm{.}}\,}}{\rm{ \times }}\,\frac{{{\rm{1}}\cancel{{{\rm{mol}}\,{\rm{Mor}}{\rm{.}}}}}}{{{\rm{285}}{\rm{.3}}\,\cancel{{{\rm{g}}\,{\rm{Mor}}{\rm{.}}}}}}\;{\rm{ \times }}\,\frac{{{\rm{6}}{\rm{.022}}\;{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{23}}}}\;\cancel{{{\rm{Mor}}{\rm{.}}\,{\rm{molecules}}}}}}{{{\rm{1}}\,\cancel{{{\rm{mol}}\,{\rm{Mor}}{\rm{.}}}}}}\;{\rm{ \times }}\,\frac{{{\rm{17}}\;{\rm{C}}\,{\rm{atoms}}}}{{{\rm{1}}\,\cancel{{{\rm{molecule}}\,{\rm{Mor}}{\rm{.}}}}}}{\rm{ = }}\;{\rm{1}}{\rm{.25}}\;{\rm{ \times }}\,{\rm{1}}{{\rm{0}}^{{\rm{24}}}}\;\;\;\]

30.

Isopropyl alcohol, also known as isopropanol, has found a widespread application in the preparation of pharmaceutical products. Answer the following questions considering that the molecular formula of isopropanol is C₃H₈O.

a) How many moles of C₃H₈O are contained in a 12.0 g sample of the alcohol?
b) How many molecules of C₃H₈O are contained in a 12.0 g sample of the alcohol?
c) How many atoms of oxygen are contained in a 12.0 g sample of the isopropyl alcohol (C₃H₈O)?
d) How many atoms of carbon are contained in a 12.0 g sample of the isopropyl alcohol (C₃H₈O)?

answer

a) 0.200 moles of C₃H₈O

answer

b) 1.20 x 10²³ molecules of C₃H₈O

answer

c) 1.20 x 10²³oxygen atoms

answer

d) 3.60 x 10²³ carbon atoms

video

31.

Check Also

Atoms, Molecules, and Ions

Stoichiometry

Converting Mass to Moles

Moles of Molecules from the Mass

Moles of a Specific Atom

Converting Moles to Mass

Practice

Calculating Moles from Mass

Calculating Mass from Moles

Calculating the Number of Molecules from the Moles

Calculating the Number of Molecules from the Mass

Calculating the Number of Atoms

Leave a Comment Cancel reply