In the previous post, we discussed the titration of 25.0 mL of 0.100 M strong acid HCl with 0.100 M NaOH. Today, we will focus on the titration of a weak acid with strong bases, so we can still use NaOH and replace the HCl with acetic acid. Let’s keep the concentrations identical and consider the titration of 25.0 mL of 0.100 M acetic acid, CH3CO2H with 0.100 M NaOH:
pH Before Adding the Base
Before the titration begins, there is only acetic acid in the solution and some of it is dissociated according to the following equation:
CH3CO2H(aq) ⇆ CH3CO2–(aq) + H+(aq)
It is a weak acid, and therefore, we’ll need to set up an ICE table and use the Ka value to determine the concentration of H+ ions. Review calculating the pH of a weak acid if you need to here.
We can set the molarity of ionized acid as x mol/l.
|
|
[CH3CO2H] |
[CH3CO2–] |
[H+] |
|
Initial |
0.100 |
0 |
0 |
|
Change |
-x |
+x |
+x |
|
Equil |
0.100 – x |
x |
x |
Next, we write the equilibrium constant expression and make an approximation that x << 0.100, therefore, 0.100 – x ≈ 0.100:
\[{K_{\rm{a}}}\; = \;\frac{{{\rm{[C}}{{\rm{H}}_{\rm{3}}}{\rm{C}}{{\rm{O}}_{\rm{2}}}^{\rm{ – }}{\rm{][}}{{\rm{H}}^{\rm{ + }}}{\rm{]}}}}{{{\rm{[C}}{{\rm{H}}_{\rm{3}}}{\rm{C}}{{\rm{O}}_{\rm{2}}}{\rm{H]}}}}\; = \;\frac{{\left( {\rm{x}} \right)\left( {\rm{x}} \right)}}{{0.100\, – \; \times }}\; \approx \;\frac{{{ \times ^{\rm{2}}}}}{{0.100\,}}\; = \;1.7\; \times \;{10^{ – 5}}\]
x = 0.0013, so the pH = -log0.0013 = 2.88
Notice that the pH is higher than what we had for the solution of HCl because the solution is not as acidic.
pH after Adding 5.00 mL NaOH
Write the neutralization reaction to do the calculations:
CH3CO2H(aq) + NaOH(aq) → CH3CO2Na(aq) + H2O(l)
The ionic form of the equation is:
CH3CO2H(aq) + OH–(aq) → CH3CO2–(aq) + H2O(l)
Let’s now calculate the initial moles of the acid and the moles of NaOH in the added 5.00 mL solution:
\[{\rm{n}}\,{\rm{(C}}{{\rm{H}}_{\rm{3}}}{\rm{C}}{{\rm{O}}_{\rm{2}}}{\rm{H)}}\;{\rm{ = }}\,{\rm{0}}{\rm{.0250}}\,\cancel{{\rm{L}}}\,{\rm{ \times }}\,\frac{{{\rm{0}}{\rm{.10}}\,{\rm{mol}}}}{{{\rm{1}}\,\cancel{{\rm{L}}}}}\,{\rm{ = }}\,{\rm{0}}{\rm{.00250}}\,{\rm{mol}}\]
\[{\rm{n}}\,{\rm{(NaOH)}}\;{\rm{ = }}\,{\rm{0}}{\rm{.00500}}\,\cancel{{\rm{L}}}\,{\rm{ \times }}\,\frac{{{\rm{0}}{\rm{.10}}\,{\rm{mol}}}}{{{\rm{1}}\,\cancel{{\rm{L}}}}}\, = \,{\rm{0}}{\rm{.000500}}\,{\rm{mol}}\]
According to the balanced equation, this is how many moles of CH3CO2H will react too because of the 1:1 mole ratio.
To find the remaining amount of CH3CO2H in the solution, we subtract the reacted moles from its initial moles. Therefore, there will be 0.00250 – 0.000500 mol = 0.00200 mol CH3CO2H.
You can also make a little ICE table to visualize this:
|
|
mol OH– |
mol CH3CO2H |
|
Before Addition |
≈ 0 |
0.00250 |
|
Added |
0.000500 |
– |
|
Remaining |
≈ 0 |
0.00200 |
Up to this point, everything is identical to what we did for the strong acid-base titrations.
So, what is Different with Weak Acid-Base Titrations?
The main difference when comparing the weak acid-base titrations with strong acid-base titrations is that there is a conjugate base of a weak acid forming here.
CH3CO2H(aq) + OH–(aq) → CH3CO2–(aq) + H2O(l)
Remember, these are strong enough to react with water and affect the pH which was not the case when NaCl formed in the titration of HCl with NaOH. The acetate ion is the conjugate base of a weak and therefore, makes the solution basic by itself.
As a result of this, after the addition of 5.00 mL NaOH, the solution turns into a buffer since it contains a weak acid, CH3CO2H, its conjugate base CH3CO2–.
Therefore, the pH is calculated using the Henderson–Hasselbalch Equation like we did it for buffer solutions.
Set up an ICE table to determine the concentration of the acid and the conjugate base:
|
|
mol OH– |
mol CH3CO2H |
mol CH3CO2– |
|
Before Addition |
≈ 0 |
0.00250 |
0 |
|
Added |
0.000500 |
– |
– |
|
Remaining |
≈ 0 |
0.00200 |
0.000500 |
\[{\rm{pH}}\; = \;{\rm{p}}{K_{\rm{a}}}\;{\rm{ + }}\;{\rm{log}}\frac{{{\rm{[C}}{{\rm{H}}_{\rm{3}}}{\rm{C}}{{\rm{O}}_{\rm{2}}}^{\rm{ – }}{\rm{]}}}}{{{\rm{[C}}{{\rm{H}}_{\rm{3}}}{\rm{C}}{{\rm{O}}_{\rm{2}}}{\rm{H]}}}}\]
The pKa of acetic acid would be:
pKa = -log Ka = -log 1.70 x 10-5 = 4.76
\[{\rm{pH}}\; = \;4.76\; + \,{\rm{log}}\frac{{{\rm{0}}{\rm{.000500}}\;}}{{{\rm{0}}{\rm{.00200}}\;}}\; = \,4.15\]
Notice that we used the moles instead of the concentrations in the Henderson–Hasselbalch Equation, and this is because they would have to be divided by the same number (volume) giving the same result.
Using this strategy, we calculate the pH after the addition of 10 – 25 mL NaOH solution.
At some point, right after passing the equivalence point, let’s after the addition of 30 mL NaOH, the solution is no longer a buffer, as it does not contain a weak acid anymore. This is where the pH is dictated by the acetate ion, and it is calculated like we did for the pH of weak bases. Check this article: pH of a Weak Base, and also problem 35 in the acid-base practice problems which specifically calculates the pH of sodium acetate.
For now, let’s use the following data for the pH values during the titration.
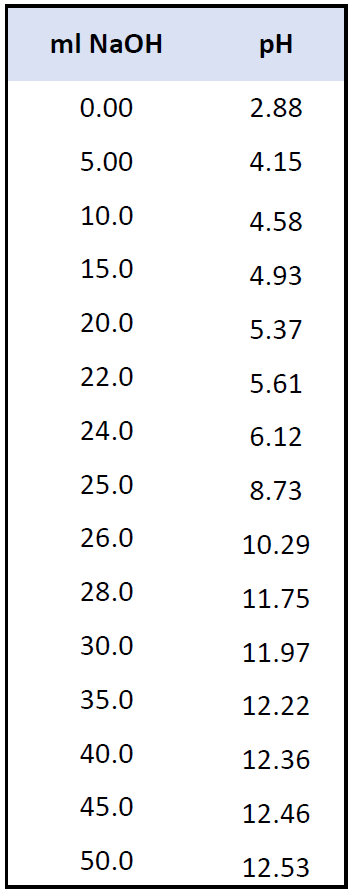
And here is the graph we obtain by plotting the values of the pH and the volume added NaOH solution:
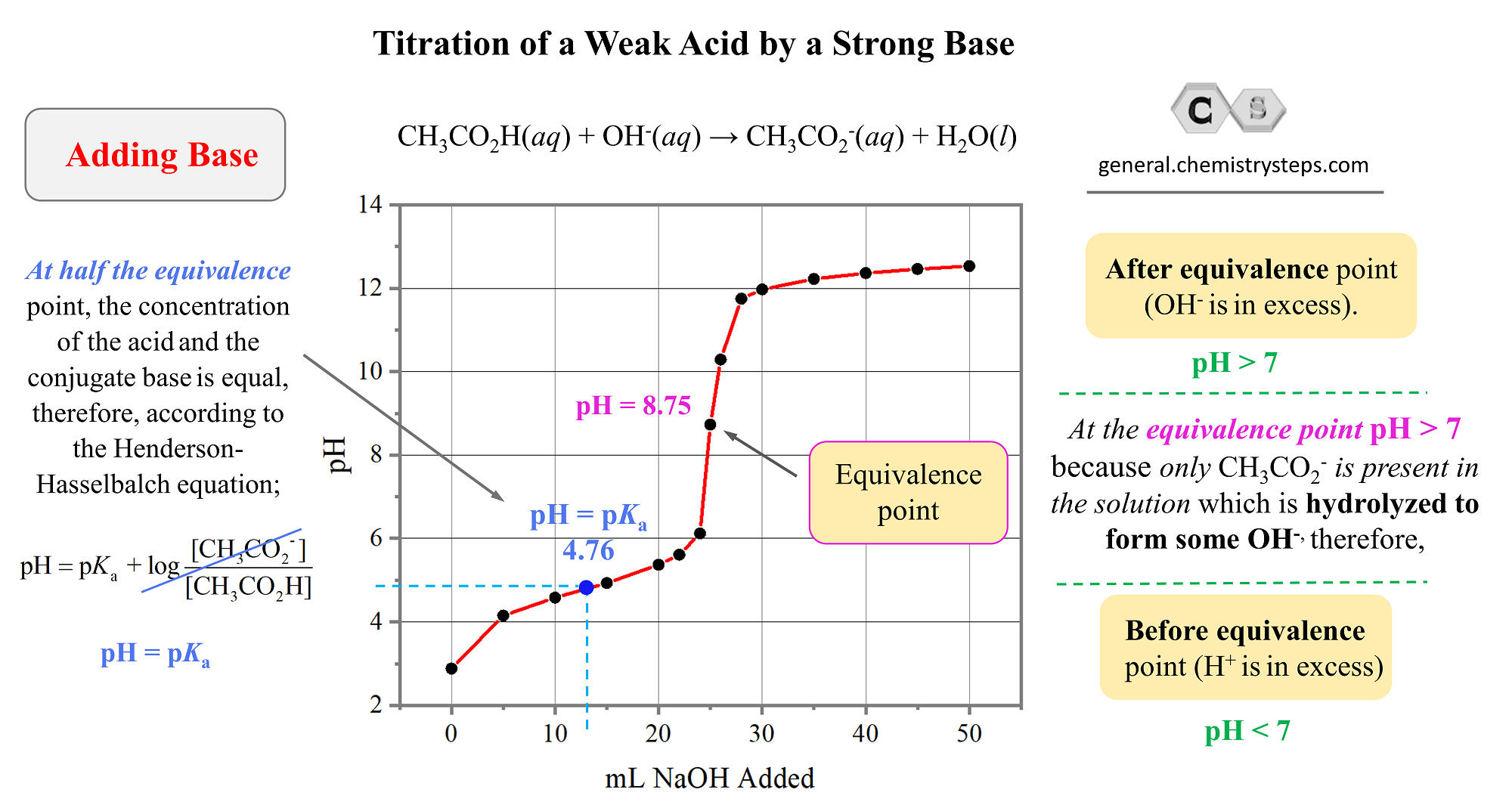
So, what key information and patterns do we see in the graph?
- Notice first, that the pH of the initial solution is not as low as it was in the case of a strong acid. This is expected because the percent ionization of weak acids is very small.
- Like in strong acid-base titrations, before reaching the equivalence point, the pH goes up as the base is added.
- The equivalence point is still reached when the moles of the base is equal to the moles of the acid in the solution. That is when all the acetic acid has been neutralized.
- What is interesting, and different from the strong acid-base titrations, is that the pH at the equivalence point is not 7. It is 8.75, and this is because of the accumulated acetate ion which is formed as the acetic acid reacts with NaOH. It is a salt of a weak acid, and a strong base, therefore, it increases the pH. Go over the acid-base properties of salts, if this is still not clear.
CH3CO2H(aq) + OH–(aq) → CH3CO2–(aq) + H2O(l)
Makes the solution basic
- Remember that in the reaction of HCl and NaOH, there was NaCl forming which is a salt of strong and a strong base, therefore has no effect on the pH.
NaOH(aq) + HCl (aq) → NaCl(aq) + H2O(l)
pH neutral salt
- Another interesting observation is that at half the equivalence point, the pH is equal to the pKa of the acid. Half the equivalence point means half of the acid initially present in the solution has reacted with the base and this, in turn, means that the concentration of the acetate ion becomes equal to the remaining 50% of the acid.
How does this make pH = pKa? Remember from the pH of buffer solutions that when [HA] = [A–], the logarithm term becomes zero, and therefore, pH becomes equal to the pKa.
In this example, at half the equivalence point, the amount of the acid is:
n (CH3CO2H) = 0.00250 ÷ 2 = 0.00125 mol
According to the balance chemical equation, there would be 0.00125 mol acetate ion formed, and therefore, the Henderson–Hasselbalch is:
\[{\rm{pH}}\; = \;{\rm{p}}{K_{\rm{a}}}\;{\rm{ + }}\;\cancel{{{\rm{log}}\frac{{0.00125}}{{0.00125}}}}\; = \,{\rm{p}}{K_a}\, = \;4.76\]
After the equivalence point, when about 30 mL of NaOH has been added, the OH– ions start to predominate in the solution. The effect of the acetate ion, CH3CO2– on the pH is negligible relative to the one of excess NaOH. Remember, it is not a buffer solution anymore and at this point, the pH is calculated like we’d for a solution of NaOH.
For example, to calculate the pH after the addition of 35.0 mL of NaOH solution, we need to determine how much OH– ions are left in the solution.
The number of NaOH moles in this portion of solution is:
\[{\rm{n}}\,{\rm{(NaOH)}}\;{\rm{ = }}\,{\rm{0}}{\rm{.0300}}\,\cancel{{\rm{L}}}\,{\rm{ \times }}\,\frac{{{\rm{0}}{\rm{.10}}\,{\rm{mol}}}}{{{\rm{1}}\,\cancel{{\rm{L}}}}}\, = \,{\rm{0}}{\rm{.00300}}\,{\rm{mol}}\]
The 25.0 mL of 0.100 M CH3CO2H would be completely neutralized, and the difference of the moles is how much NaOH we’d have in the solution:
n (NaOH) = 0.00300 – 0.0025 = 0.000500 mol OH–
Make sure to add the volumes before calculating the concentration:
\[{\rm{M}}\;{\rm{(NaOH)}}\,{\rm{ = }}\,\frac{{{\rm{0}}{\rm{.000500 mol}}}}{{{\rm{0}}{\rm{.0250}}\,{\rm{L}}\,{\rm{ + }}\,{\rm{0}}{\rm{.0350}}\,{\rm{L}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.00833}}\,{\rm{mol/L}}\]
pOH = -log 0.00833 = 2.08
And using the pH-pOH relationship, we can determine the pH:
pH + pOH = 14
pH = 14 – pOH = 14 – 2.08 = 11.92
And this should conclude the most important parts of the weak acid titrations with a strong base. In the next post, we will discuss the titration of a weak base by a strong acid.
Check Also
- Buffer Solutions
- The Henderson–Hasselbalch Equation
- The pH of a Buffer Solution
- Preparing a Buffer with a Specific pH
- The Common Ion Effect
- The pH and pKa Relationship
- Strong Acid–Strong Base Titrations
- Titration of a Weak Base by a Strong Acid
- Titration of Polyprotic Acids
- Buffer Solutions Practice Problems
- Ksp and Molar Solubility
- The Effect of a Common Ion on Solubility
- The Effect of pH on Solubility
- Will a Precipitate Form? Ksp and Q
- Ksp and Molar Solubility Practice Problems
