In the previous post, we talked about the solubility and solubility product constant (Ksp) of ionic compounds with low solubility.
For example, the dissolution equation and the Ksp for CaF2 are:
CaF2(s) ⇆ Ca2+(aq) + 2F–(aq)
Ksp = [Ca2+][ F–]2 = 3.9 x 10-11
By assigning x mol/L as the concentration of CaF2 dissolved in a saturated solution, we were able to determine the molar solubility of CaF2 from the Ksp.
Setting up an ICE table helps determine the concentrations correctly.
x x 2x
CaF2(s) ⇆ Ca2+(aq) + 2F–(aq)
| [Ca2+] | [F–] | ||
| Initial | 0 | 0 | |
| Change | +x | +2x | |
| Equil | x | 2x | |
So, the expression for Ksp can be written as:
Ksp = [Ca2+][ F–]2 = (x)(2x) = 3.9 x 10-11
Therefore,
(x)(2x)2 = 3.9 x 10-11
4x3 = 3.9 x 10-11
x = 2.1 x 10-4
2.1 x 10-4 mol/L is the concentration of dissolved CaF2 because it is in 1:1 ratio with Ca2+, and this is the molar solubility of CaF2.
The Effect of a Common Ion on Solubility
Let’s now assume that the solution of CaF2 contains Ca(NO3)2 with a concentration of 0.20 M. What is the molar solubility of CaF2 in this solution?
Before doing the calculations, we can predict the solubility will go down because Ca(NO3)2 is a strong electrolyte and completely dissociates into Ca2+ and NO3– ions. Importantly, the Ca2+ is also formed when CaF2 dissolves in water, so it is a common ion, and as we discussed earlier it pushes the equilibrium to the opposite direction according to the Le Châtelier’s principle.
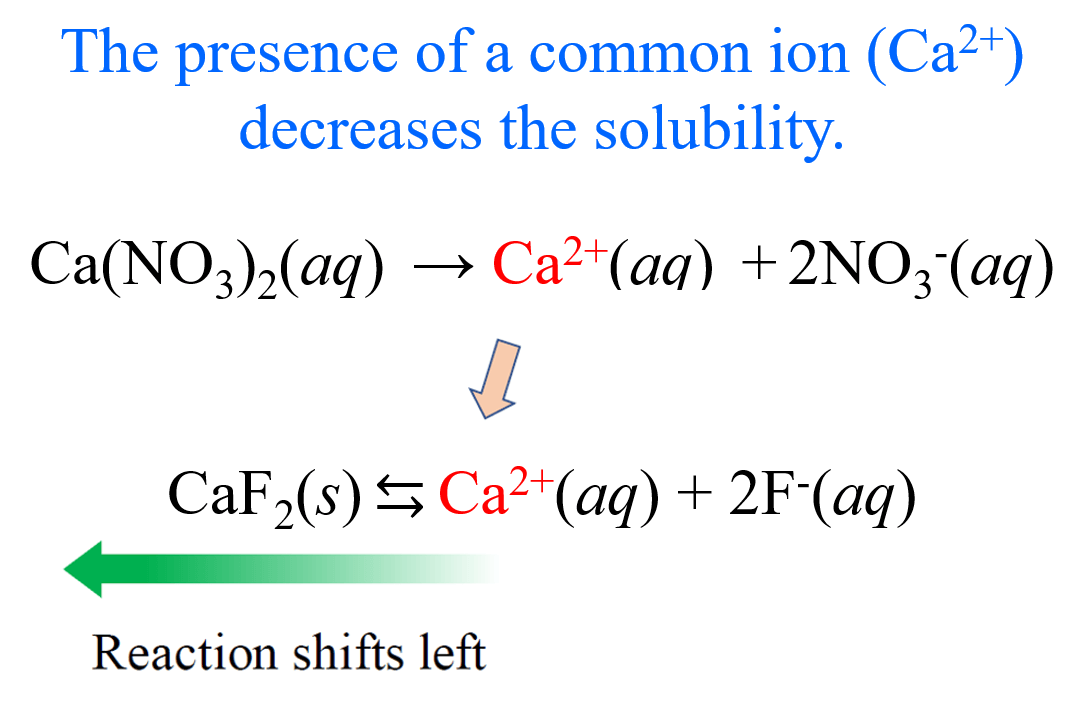
And now, let’s calculate the molar solubility of CaF2. It is going to be the same procedure, except the initial concentration of Ca2+ ions is not zero since the dissociation of Ca(NO3)2 produces an equivalent amount of the cation.
0.20 0.20 0.40
Ca(NO3)2 (aq) ⇆ Ca2+(aq) + 2NO3–(aq)
x x 2x
CaF2(s) ⇆ Ca2+(aq) + 2F–(aq)
| [Ca2+] | [F–] | ||
| Initial | 0.20 | 0 | |
| Change | +x | +2x | |
| Equil | 0.20 + x | 2x | |
So, the expression for Ksp is:
Ksp = [Ca2+][ F–]2 = (0.20 + x)(2x)2 = 3.9 x 10-11
Now, because the ionization of CaF2 is negligible compared to the one of Ca(NO3)2, we assume that 0.20 + x ≈ 0.20, and the simplified equation will be:
(0.20)(2x)2 = 3.9 x 10-11
0.80x2 = 3.9 x 10-11
Therefore,
x = 7.0 x 10-6
The x is very small compared to 0.20, and therefore, the approximation was valid, and 7.0 x 10-6 M is the molar solubility of CaF2 in the presence of 0.20 M Ca(NO3)2. As expected it is lower than the solubility of CaF2 in pure water (2.1 x 10-4).
Let’s do another example, where the solution contains 0.15 M NaF.
In this case, the common ion is F- and therefore, its initial concentration is going to be equal to 0.15 M since NaF is a strong electrolyte and completely dissociates in aqueous solutions.
0.15 0.15 0.15
NaF(aq) ⇆ Na+(aq) + F–(aq)
x x 2x
CaF2(s) ⇆ Ca2+(aq) + 2F–(aq)
| [Ca2+] | [F–] | ||
| Initial | 0 | 0.15 | |
| Change | +x | +2x | |
| Equil | x | 0.15 + 2x | |
So, the expression for Ksp is:
Ksp = [Ca2+][ F–]2 = (x)(0.15 + 2x)2 = 3.9 x 10-11
Now, because the ionization of CaF2 is negligible compared to the one of NaF, we assume that 0.15 + x ≈ 0.15, and the simplified equation will be:
(x)(0.15)2 = 3.9 x 10-11
0.0225x = 3.9 x 10-11
Therefore,
x = 1.7 x 10-9
The x is very small compared to 0.15, and therefore, the approximation was valid, and 1.7 x 10-9 M is the molar solubility of CaF2 in the presence of 0.15 M NaF. As expected it is lower than the solubility of CaF2 in pure water (2.1 x 10-4).
So, to summarize, remember that in general, the solubility of a slightly soluble ionic compound decreases with the presence of a common ion in the solution.
Check Also
- Buffer Solutions
- The Henderson–Hasselbalch Equation
- The pH of a Buffer Solution
- Preparing a Buffer with a Specific pH
- The Common Ion Effect
- The pH and pKa Relationship
- Strong Acid–Strong Base Titrations
- Titration of a Weak Acid by a Strong Base
- Titration of a Weak Base by a Strong Acid
- Titration of Polyprotic Acids
- Buffer Solutions Practice Problems
- Ksp and Molar Solubility
- The Effect of pH on Solubility
- Will a Precipitate Form? Ksp and Q
- Ksp and Molar Solubility Practice Problems
