The common ion effect is an example of the Le Châtelier’s principle when altering the equilibrium by changing the concentration of a component.
Remember, adding a reactant produces more product by shifting the equilibrium to the right, and adding a product, produces more of the reactants because the equilibrium shifts to the left:
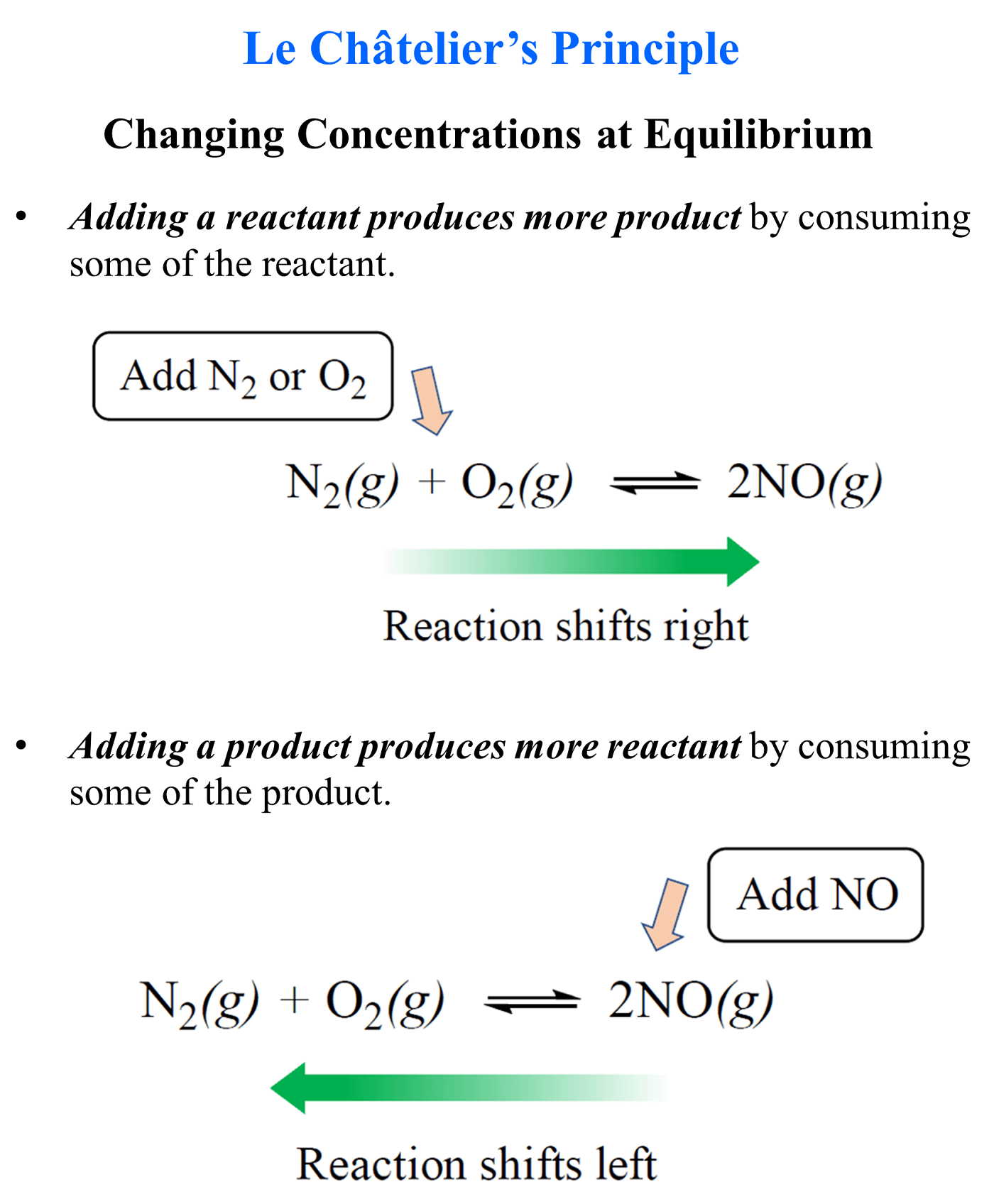
So, this same principle applies to aqueous equilibrium when there is a component added to the solution.
For example, when acetate ion is added to a solution of acetic acid, it suppresses the dissociation of the acid. The acetate ion is the common ion because it is already present in the solution:

This effect can be seen by comparing the pH’s of both solutions; one with only acetic acid and the other when with added acetate ion.
For example, the pH of 0.50 M solution of acetic acid (Ka = 1.7 x 10-5) is calculated to be 2.5 as follows:
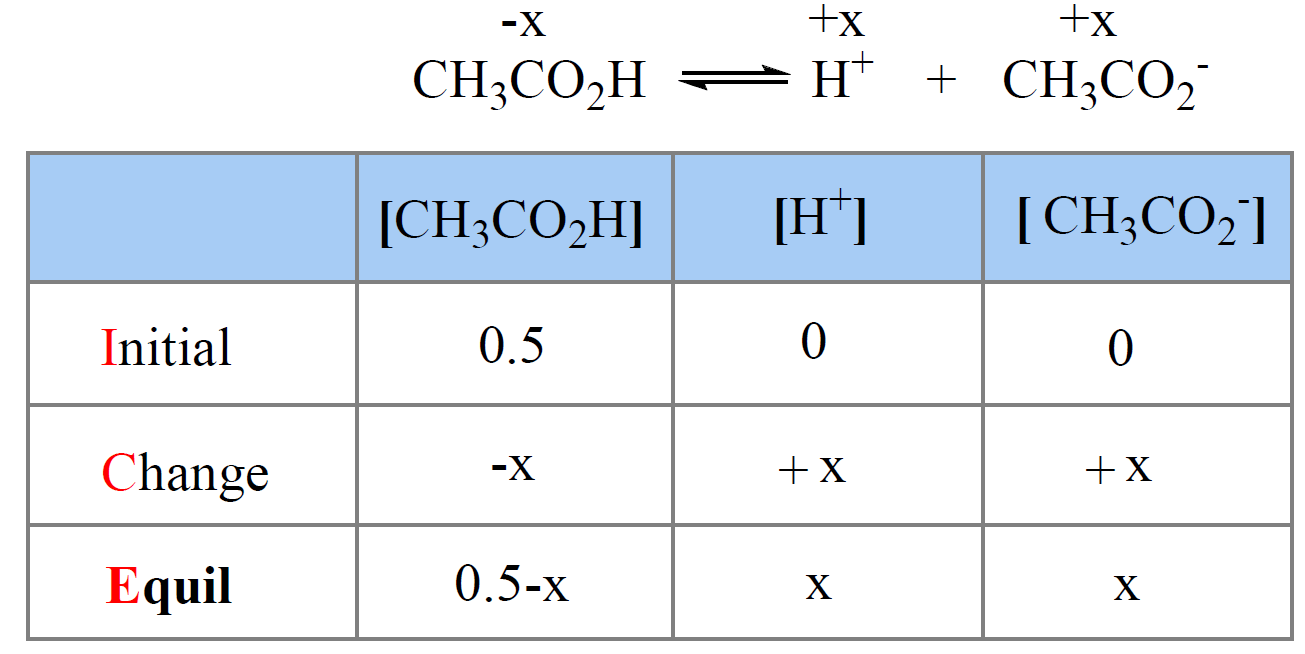
We write the equilibrium constant expression and make an approximation that x << 0.50, therefore, 0.5 – x ≈ 0.5:
\[{K_{\rm{a}}}\; = \;\frac{{{\rm{[C}}{{\rm{H}}_{\rm{3}}}{\rm{C}}{{\rm{O}}_{\rm{2}}}^{\rm{ – }}{\rm{][}}{{\rm{H}}^{\rm{ + }}}{\rm{]}}}}{{{\rm{[C}}{{\rm{H}}_{\rm{3}}}{\rm{C}}{{\rm{O}}_{\rm{2}}}{\rm{H]}}}}\; = \;\frac{{\left( {\rm{x}} \right)\left( {\rm{x}} \right)}}{{0.5\, – \;x}}\; \approx \;\frac{{{{\rm{x}}^{\rm{2}}}}}{{0.5\,}}\; = \;1.7\; \times \;{10^{ – 5}}\]
x = 0.0029, so the pH = -log0.0029 = 2.5
You can read more about calculating the pH of a buffer solution here, but for the purpose of explaining the common ion effect, we are now showing it very briefly.
On the other hand, the pH of an acetic acid buffer containing 0.50 M acetic acid and 0.20 M of its conjugate base sodium acetate (CH3CO2Na), is calculated to be 4.37 using the Henderson–Hasselbalch equation:
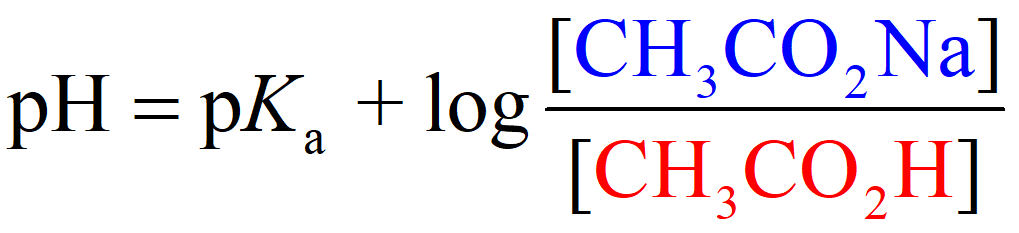
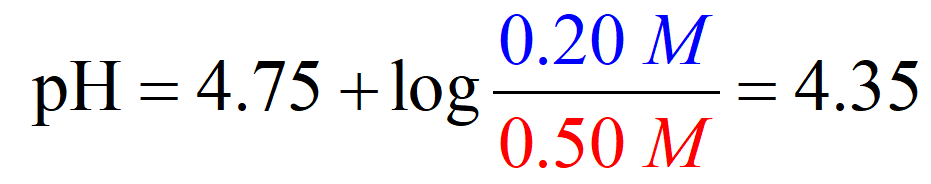
So, when the acid is in the solution by itself, it dissociates more than it does when its conjugate base is present as well. The common ion suppresses the dissociation and thus less H3O+ is formed and therefore, the pH goes up (less acidic).
Check Also
- Buffer Solutions
- The Henderson–Hasselbalch Equation
- The pH of a Buffer Solution
- Preparing a Buffer with a Specific pH
- The pH and pKa Relationship
- Strong Acid–Strong Base Titrations
- Titration of a Weak Acid by a Strong Base
- Titration of a Weak Base by a Strong Acid
- Titration of Polyprotic Acids
- Buffer Solutions Practice Problems
- Ksp and Molar Solubility
- The Effect of a Common Ion on Solubility
- The Effect of pH on Solubility
- Will a Precipitate Form? Ksp and Q
- Ksp and Molar Solubility Practice Problems
