The solubility of almost any ionic compound is affected by the pH of a solution. The effect is more pronounced when one or both of the ions in the compound are slightly basic or acidic. For example, magnesium hydroxide, an ionic compound with low solubility, produces a saturated solution with a pH of 10.52:
Mg(OH)2(s) ⇆ Mg2+(aq) + 2OH–(aq)
The OH– is a basic ion and it turns out that if we decrease the pH of the solution, the solubility increases. On the contrary, the solubility is decreased in a more basic solution.
This is still explained by Le Châtelier’s principle. Higher concentration of OH– ions push the reaction to the left in accordance with the common ion effect. At lower pH, some of the OH– ions are neutralized which drives the reaction to the right:
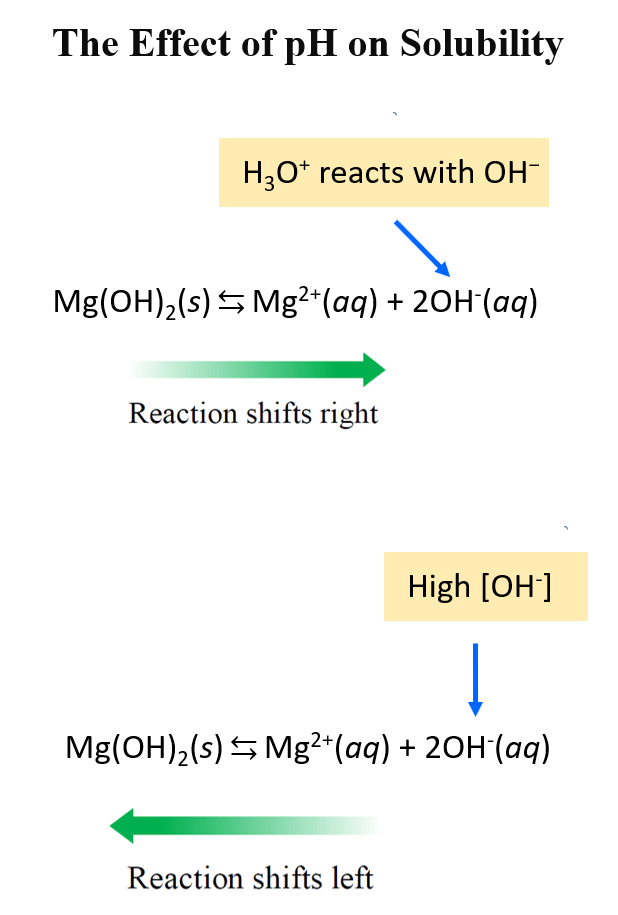
For example, let’s calculate the concentration of Mg2+ ions at pH 10.52 which is its saturated solution in pure water, and pH 9.5. The solubility product of Mg(OH)2 is:
Ksp = [Mg2+][ OH–]2 = 1.8 x 10-11
Now, when working with the solubility of hydroxides, it is a good idea to do the calculations based on the concentrations of OH– ions. So, instead of assigning x mol/L as the concentration of Mg(OH)2 dissolved in a saturated solution and setting up an ICE table as we’d normally do, we determine the concentration of OH– ions based on the pH, and do not automatically assume that the concentration of the cation is in a stoichiometric ratio.
Let’s do it both ways so we can address the difference and the reasons why going based on the pH value is more accurate.
Approach 1 – Doing it like for other ionic compounds:
x x 2x
Mg(OH)2(s) ⇆ Mg2+(aq) + 2OH–(aq)
| [Mg2+] | [OH–] | ||
| Initial | 0 | 0 | |
| Change | +x | +2x | |
| Equil | x | 2x | |
So, the expression for Ksp can be written as:
Ksp = [Mg2+][OH–]2 = (x)(2x) = 1.8 x 10-11
Therefore,
(x)(2x)2 = 1.8 x 10-11
4x3 = 1.8 x 10-11
x = 1.7 x 10-4
So, [Mg2+] = 1.7 x 10-4 mol/L, and because it is in a 1:1 ratio with Mg(OH)2, this is also the molar solubility of Mg(OH)2.
Approach 2 – Doing it based on pH and [OH–]:
To calculate [Mg2+] at a given pH, we first need to determine the [OH–] using the pH and pOH relationship.
pH + pOH = 14
pOH = 14 – pH = 14 – 10.52 = 3.48
To find the [OH–], we take the antilog of pOH:
pOH = -log [OH–]
[OH–] = 10-pOH
[OH–] = 10-3.48 = 3.31 x 10-4 M
Now the important part on the specifics of hydroxides: We cannot always calculate the concentration of the cation simply by relying on its stoichiometric ratio with [OH–] because some of the hydroxide ions are coming from the dissociation of water.
H2O(l) ⇆ H+(aq) + OH–(aq)
Remember, in pure water the concentration of OH– ions is already 10-7 M.
And although Mg(OH)2 is a strong enough base to ignore the contribution of OH– from water, doing this at a lowered pH may not be a good approximation.
On the contrary, for very weak hydroxides (Ksp < 10-25), the OH– is considered to be coming from water only. The hydroxide dissolves so little that it produces far less OH– than water does.
To avoid possible mistakes, we go based on the pH because it tells the concentration of the OH- ions which already includes the contribution from water and the hydroxide itself.
Therefore, in this case, we assign [Mg2+] = [Mg(OH)2] = x M.
Ksp = [Mg2+][OH–]2 = (x)(3.31 x 10-4)2 = 1.8 x 10-11, x = 1.64 x 10-4 M
Mg2+] at pH 9.5
First determine the [OH–] using the pH and pOH relationship.
pH + pOH = 14
pOH = 14 – pH = 14 – 9.5 = 4.5
To find the [OH–], we take the antilog of pOH:
pOH = -log [OH–]
[OH–] = 10-pOH
[OH–] = 10-4.5 = 3.2 x 10-5
And now, we can plug this value in the expression of Ksp to determine [Mg2+]:
Ksp = [Mg2+][OH–]2 = (x)( 3.2 x 10-5)2 = 1.8 x 10-11
x = 0.018 = 1.8 x 10-2
We see that the concentration of Mg2+ ions has increased one hundred times by decreasing the pH from 10.52 to 9.5.
So, this was an example of pH affecting the solubility of a compound with a basic ion. And, in general, the solubility of a compound containing a basic anion (that is, the anion of a weak acid) increases with increasing acidity (decreasing pH).
Other common ions with basic properties are, F–, PO43–, CN–, S2–, and CO32–. Therefore, the pH will have an identical effect on their solubility.
Practice
Determine the Ksp for calcium hydroxide, Ca(OH)2 if its saturated solution has a pH of 12.35.
Ksp = 5.6 x 10-6
The dissociation equation and the corresponding expression for the solubility product are:
Ca(OH)2(s) ⇆ Ca2+(aq) + 2OH–(aq)
Ksp = [Ca2+][OH–]2
Now, to determine the [OH–], we first determine the pOH using the pH and pOH relationship.
pH + pOH = 14
pOH = 14 – pH = 14 – 12.35 = 1.65
To find the [OH–], we take the antilog of pOH:
pOH = -log [OH–]
[OH–] = 10-pOH
[OH–] = 10-1.65 = 0.0224 M
The concentration of Ca2+ ions is half of this because of the 1:2 ratio. Therefore, [Ca2+] = 0.0224 ÷ 2 = 0.0112 M.
And now, we can plug these values in the expression of Ksp:
Ksp = [Ca2+][OH–]2 = (0.0112)( 0.0224)2 = 5.6 x 10-6
The Ksp for chromium (III) hydroxide, Cr(OH)3 is 6.7 x 10-31. Calculate the solubility of Cr(OH)3 in g/L of water.
6.9 x 10-8 g/L
The dissociation equation and the corresponding expression for the solubility product are:
Cr(OH)3(s) ⇆ Cr3+(aq) + 3OH–(aq)
Ksp = [Cr3+][OH–]3
Now, one thing to keep in mind when working with hydroxides with very low solubility, is that the presence of OH– ions is mostly due to the autoionization of water. Remember, in pure water, the [OH–] = 1.0 x 10-7 M, therefore, this is going to be the initial concentration of OH– in the ICE table:
Assuming x M for the solubility of Cr(OH)3, we can set up an ICE table:
x x 3x
Cr(OH)3(s) ⇆ Cr3+(aq) + 3OH–(aq)
| [Cr3+] | [OH–] | |
| Initial | 0 | 1.0 x 10-7 |
| Change | + x | + 3x |
| Equil | x | 1.0 x 10-7 + 3x |
Entering the numbers into the Ksp expression, we get that it is:
Ksp = [Cr3+][OH–]3 = (x) (1.0 x 10-7 + 3x)3= 6.7 x 10-31
Now, because the ionization of Cr(OH)3 is very little, we assume that 1.0 x 10-7 + 3x ≈ 1.0 x 10-7. Therefore,
(1.0 x 10-7)3 x = 6.7 x 10-31
x = 6.7 x 10-10
This is the solubility of Cr(OH)3 in mol/L, and the assumption is valid because 6.7 x 10-10 << 1.0 x 10-7.
To determine the solubility in g/L, we multiply it by the molar mass of Cr(OH)3:
\[{\rm{6}}{\rm{.7 x 1}}{{\rm{0}}^{{\rm{ – 10}}}}\,\frac{{\cancel{{{\rm{mol}}}}}}{{\rm{L}}}\;{\rm{ \times }}\,\frac{{{\rm{103}}\,{\rm{g}}}}{{{\rm{1}}\,\cancel{{{\rm{mol}}}}}}\, = \,6.9\; \times \,{10^{ – 8}}\,{\rm{g/L}}\]
Calculate the molar solubility of Al(OH)3 (Ksp = 2.0 x 10-32) in each of the following solutions.
a) Pure water
b) a solution buffered at pH = 6.0
c) a solution buffered at pH = 10.0
2.0 x 10-11
2.0 x 10-8
2 x 10-20
a) The dissociation equation and the corresponding expression for the solubility product are:
Al(OH)3(s) ⇆ Al3+(aq) + 3OH–(aq)
Ksp = [Al3+][OH–]3
Again, when working with hydroxides with low solubility, remember that the presence of OH– ions is mostly due to the autoionization of water. In pure water, the [OH–] = 1.0 x 10-7 M, therefore, this is going to be the initial concentration of OH– in the ICE table:
Assuming x M for the solubility of Al(OH)3, we can set up an ICE table:
x x 3x
Al(OH)3(s) ⇆ Al3+(aq) + 3OH–(aq)
| [Al3+] | [OH–] | |
| Initial | 0 | 1.0 x 10-7 |
| Change | + x | + 3x |
| Equil | x | 1.0 x 10-7 + 3x |
Entering the number into the Ksp expression, we get that it is:
Ksp = [Al3+][OH–]3 = (x) (1.0 x 10-7 + 3x)3= 2 x 10-32
Because the ionization of Al(OH)3 is very little, we assume that 1.0 x 10-7 + 3x ≈ 1.0 x 10-7. Therefore,
(1.0 x 10-7)3 x = 2.0 x 10-32
x = 2.0 x 10-11
This is the solubility of Al(OH)3 in mol/L, and the assumption is valid because 2.0 x 10-11 << 1.0 x 10-7.
b) Since the pH is given, we can calculate the pOH and therefore, the [OH–] which already includes the contribution from the water autoionization. So, to determine the [OH–] we are going to use the pH and pOH relationship.pH + pOH = 14
pOH = 14 – pH = 14 – 6.0 = 8.0
To find the [OH–], we take the antilog of pOH:
pOH = -log [OH–]
[OH–] = 10-pOH
[OH–] = 1.0 x 10-8.0
Note: We cannot assume that the concentration of Al3+ ions is the third of [OH–] simply relying on the 1:3 ratio because some of the OH– ions are coming from the dissociation of water. Therefore, we assign [Al3+] = [Al(OH)3] = x M.
x x 3x
Al(OH)3(s) ⇆ Al3+(aq) + 3OH–(aq)
| [Al3+] | [OH–] | |
| Initial | 0 | 1.0 x 10-8.0 |
| Change | + x | x is already included |
| Equil | x | 1.0 x 10-8.0 |
And now, we can plug these values in the expression of Ksp:
Ksp = [Al3+][OH–]3 = (x)(1.0 x 10-8.0 )3 = 2.0 x 10-32
x = 2.0 x 10-8
So, there will be 2 x 10-8 M Al(OH)3 dissolved producing the same amount of Al3+. Let’s plug in the numbers and check if we get the correct value of the Ksp:
Ksp = [Al3+][OH–]3 = (2 x 10-8)(1.0 x 10-8.0 )3 = 2 x 10-32
Notice that in part (a), we found that the solubility of Al(OH)3 at pH 7 was 2.0 x 10-11, and as expected, it has increased (2.0 x 10-8) by decreasing the pH to 6.0. Remember, the solubility of hydroxides increases with the acidity of the solution since consuming the OH– pushes the equilibrium forward according to the Le Châtelier’s principle.
c) Since the pH is given, we can calculate the pOH and therefore, the [OH–] which already includes the contribution from the water autoionization. So, to determine the [OH–] we are going to use the pH and pOH relationship.
pH + pOH = 14
pOH = 14 – pH = 14 – 10.0 = 4.0
To find the [OH–], we take the antilog of pOH:
pOH = -log [OH–]
[OH–] = 10-pOH
[OH–] = 1.0 x 10-4.0
Note: We cannot assume that the concentration of Al3+ ions is the third of this relying on the 1:3 ratio because some of the OH– ions are coming from the dissociation of water. Therefore, we assign [Al3+] = [Al(OH)3] = x M.
| [Al3+] | [OH–] | |
| Initial | 0 | 1.0 x 10-4.0 |
| Change | + x | |
| Equil | x | 1.0 x 10-4.0 |
And now, we can plug this value in the expression of Ksp:
Ksp = [Al3+][OH–]3 = (x)(1.0 x 10-4.0 )3 = 2 x 10-32
x = 2 x 10-20
So, there will be 2 x 10-20 M Al(OH)3 dissolved producing the same amount of Al3+. Let’s plug in the numbers and check if we get the correct value of the Ksp:
Ksp = [Al3+][OH–]3 = (2 x 10-20)(1.0 x 10-4.0 )3 = 2 x 10-32
In this case, when the pH is higher (larger [OH–]), the solubility of Al(OH)3 is expected to decrease since the excess of OH– pushes the equilibrium to the left (less dissolution) according to the Le Châtelier’s principle. And this is consistent with our results: the solubility in pure water vs at pH 10 is 2.0 x 10-11 : 2 x 10-20.
The Ksp for zinc hydroxide, Zn(OH)2 is 4.5 x 10-17. Determine the pH of a saturated solution of zinc hydroxide.
pH = 8.65
The dissociation equation and the corresponding expression for the solubility product are:
Zn(OH)2(s) ⇆ Zn2+(aq) + 2OH–(aq)
Ksp = [Zn2+][OH–]2
Remember, in pure water, the [OH–] = 1.0 x 10-7 M, therefore, this is going to be the initial concentration of OH– in the ICE table:
Assuming x M for the solubility of the base, we can set up an ICE table:
x x 2x
Zn(OH)2(s) ⇆ Zn2+(aq) + 2OH–(aq)
| [Zn2+] | [OH–] | |
| Initial | 0 | 1.0 x 10-7 |
| Change | + x | + 2x |
| Equil | x | 1.0 x 10-7 + 2x |
Entering the number into the Ksp expression, we get that it is:
Ksp = [Zn2+][OH–]2 = (x) (1.0 x 10-7 + 2x)2= 4.5 x 10-17
Note: The ionization of Zn(OH)2 is comparable to that of water, but because there are two OH– forming from each Zn(OH)2, we assume that 1.0 x 10-7 + 2x ≈ 2x. In other words, Zn(OH)2 is a strong enough base to ignore the contribution of OH– ions from the ionization of water. This is what we’d do for determining the [OH–] in solutions such as NaOH, KOH, LiOH, etc.
Therefore,
x(2x)2 = 4.5 x 10-17
4x3 = 4.5 x 10-17
x = 2.24 x 10-6
[OH–] is going to be two times greater; 2 x 2.24 x 10-6 = 4.48 x 10-6 mol/L.
pOH = -log 4.48 x 10-6 = 5.35
pH = 14 – 5.35 = 8.65
Check Also
- Buffer Solutions
- The Henderson–Hasselbalch Equation
- The pH of a Buffer Solution
- Preparing a Buffer with a Specific pH
- The Common Ion Effect
- The pH and pKa Relationship
- Strong Acid–Strong Base Titrations
- Titration of a Weak Acid by a Strong Base
- Titration of a Weak Base by a Strong Acid
- Titration of Polyprotic Acids
- Buffer Solutions Practice Problems
- Ksp and Molar Solubility
- The Effect of a Common Ion on Solubility
- Will a Precipitate Form? Ksp and Q
- Ksp and Molar Solubility Practice Problems