In the previous post, we discussed the titration of a weak acid, CH3CO2H with a strong base, NaOH. The main difference compared to the strong acid-base titrations was that the conjugate base of the weak acid, forming during the reaction was basic, and therefore the pH at the equivalence point was higher than 7.
CH3CO2H(aq) + OH–(aq) → CH3CO2–(aq) + H2O(l)
Makes the solution basic
So, let’s see what the titration curve looks like when a weak base such as ammonia, NH3 is titrated with a strong acid, HCl.
Suppose we have 25.0 mL of 0.100 M NH3 titrated with a 0.100 M solution of HCl.
pH Before Adding the Acid
Before the titration begins, there is only ammonia in the solution, and as a weak base, it reacts with water producing OH– ions making the solution basic. The pH is calculated based on the Kb of ammonia by setting up an ICE table:
-x +x +x
NH3(aq) + H2O(l) ⇆ NH4+(aq) + OH–(aq)
|
|
[NH3] |
[NH4+] |
[OH–] |
|
Initial |
0.100 |
0 |
0 |
|
Change |
-x |
+x |
+x |
|
Equil |
0.100 – x |
x |
x |
The expression for the equilibrium constant will then be:
\[{K_{{\rm{b}}}}\; = \,\frac{{{\rm{[N}}{{\rm{H}}_{\rm{4}}}^{\rm{ + }}{\rm{][O}}{{\rm{H}}^{\rm{ – }}}{\rm{]}}}}{{{\rm{[N}}{{\rm{H}}_{\rm{3}}}{\rm{]}}}}\; = \;\frac{{{{\rm{x}}^{\rm{2}}}}}{{{\rm{0}}{\rm{.100}}\;{\rm{ – }}\;{\rm{x}}}}\; = \;{\rm{1}}{\rm{.8 }} \times {\rm{ 1}}{{\rm{0}}^{{\rm{ – 5}}}}\]
We simplify the equation by assuming 0.100 – x ≈ 0.100
\[\;\frac{{{{\rm{x}}^{\rm{2}}}}}{{{\rm{0}}{\rm{.100}}\;}}\; = \;{\rm{1}}{\rm{.8 }} \times {\rm{ 1}}{{\rm{0}}^{{\rm{ – 5}}}}\]
Therefore, x = 0.00134
The approximation is valid, because:
\[\frac{{{\rm{0}}{\rm{.00134}}}}{{{\rm{0}}{\rm{.100}}}}\; \times \;100\% = \;{\rm{1}}{\rm{.34\% }}\]
Next, we determine the concentration of H+ ions from the relationship [OH–] · [H+] = Kw = 10-14.
\[\left[ {{{\rm{H}}^{\rm{ + }}}} \right]\;{\rm{ = }}\,\frac{{{K_{\rm{w}}}}}{{\left[ {{\rm{O}}{{\rm{H}}^{\rm{ – }}}} \right]}}\; = \,\frac{{1.0\, \times {{10}^{ – 14}}}}{{0.00134}}\, = \,7.46\, \times \,{10^{ – 12}}\]
pH = -log [H+] = -log 7.46 x 10-12 = 11.13
As expected, the solution is basic and therefore, pH 11.13 is a reasonable number.
pH Before the equivalence point
Once some of the ammonia is converted into its conjugate acid NH4+, the solution turns into a buffer since it contains a weak base and its conjugate acid. This is true approximately up until the equivalence point, where all the ammonia is converted into NH4+ at which point, the solution contains a salt of a weak base and a strong acid, and we follow the procedure for calculating the pH of a salt solution.
For now, let’s calculate the pH after the addition of 10.0 mL of HCl before the equivalence point where we still have a buffer solution.
The acid is going to react with ammonia in a stoichiometric ratio, thus producing the same amount of NH4+ ions.
HCl(aq) + NH3(aq) → NH4Cl(aq)
Therefore:
\[{\rm{n}}\,{\rm{(HCl)}}\;{\rm{ = }}\,{\rm{n}}\,{\rm{(N}}{{\rm{H}}_{\rm{3}}}{\rm{)}}\;{\rm{ = }}\,{\rm{n}}\,{\rm{(N}}{{\rm{H}}_{\rm{4}}}^{\rm{ + }}{\rm{)}}\;{\rm{ = }}\,{\rm{0}}{\rm{.0100}}\,\cancel{{\rm{L}}}\,{\rm{ \times }}\,\frac{{{\rm{0}}{\rm{.10}}\,{\rm{mol}}}}{{{\rm{1}}\,\cancel{{\rm{L}}}}}\,{\rm{ = }}\,{\rm{0}}{\rm{.00100}}\,{\rm{mol}}\]
The initial moles of ammonia are
\[{\rm{n}}\,{\rm{(N}}{{\rm{H}}_{\rm{3}}}{\rm{)}}\;{\rm{ = }}\,\,{\rm{0}}{\rm{.0250}}\,\cancel{{\rm{L}}}\,{\rm{ \times }}\,\frac{{{\rm{0}}{\rm{.10}}\,{\rm{mol}}}}{{{\rm{1}}\,\cancel{{\rm{L}}}}}\,{\rm{ = }}\,{\rm{0}}{\rm{.00250}}\,{\rm{mol}}\]
And to find the remaining moles of ammonia we subtract the reacted 0.00100 moles from the initial 0.00250 moles:
n (NH3) = 0.00250 – 0.00100 = 0.00150 mol
Note: We saw that some of the ammonia reacts with water producing OH-, however, this quantity is negligible compared to how much reacts with the acid, and therefore, we do not include it in this calculation.
So, now we need to calculate the concentrations of NH3 and NH4+ to calculate the pH using the Henderson–Hasselbalch Equation as we did it for buffer solutions.
\[{\rm{M}}\,{\rm{(N}}{{\rm{H}}_{\rm{3}}}{\rm{)}}\;{\rm{ = }}\,\frac{{{\rm{0}}{\rm{.00150}}\,{\rm{mol}}}}{{{\rm{0}}{\rm{.0250}}\,{\rm{L}}\;{\rm{ + }}\,{\rm{0}}{\rm{.0100}}\,{\rm{L}}}}\;{\rm{ = }}\,{\rm{0}}{\rm{.0429}}\,{\rm{mol/L}}\]
\[{\rm{M}}\,{\rm{(N}}{{\rm{H}}_{\rm{4}}}^{\rm{ + }}{\rm{)}}\;{\rm{ = }}\,\frac{{{\rm{0}}{\rm{.00100}}\,{\rm{mol}}}}{{{\rm{0}}{\rm{.0250}}\,{\rm{L}}\;{\rm{ + }}\,{\rm{0}}{\rm{.0100}}\,{\rm{L}}}}\;{\rm{ = }}\,{\rm{0}}{\rm{.0286}}\,{\rm{mol/L}}\]
\[{\rm{pH}}\; = \;{\rm{p}}{K_{\rm{a}}}\;{\rm{ + }}\;{\rm{log}}\frac{{{\rm{[N}}{{\rm{H}}_{\rm{3}}}{\rm{]}}}}{{{\rm{[N}}{{\rm{H}}_{\rm{4}}}^{\rm{ + }}{\rm{]}}}}\]
\[{\rm{pH}}\; = \;9.25\;{\rm{ + }}\;{\rm{log}}\frac{{{\rm{[0}}{\rm{.0429]}}}}{{{\rm{[0}}{\rm{.0286]}}}}\; = \;9.43\]
pH at Half Equivalence Point
Like in the titration of a weak acid by a strong base, the pH at half the equivalence point is going to be equal to the pKa of the acid because the logarithm term in the Henderson–Hasselbalch Equation becomes zero.
\[{\rm{pH}}\; = \;{\rm{p}}{K_{\rm{a}}}\;{\rm{ + }}\;\cancel{{{\rm{log}}\frac{{{\rm{[N}}{{\rm{H}}_{\rm{3}}}{\rm{]}}}}{{{\rm{[N}}{{\rm{H}}_{\rm{4}}}^{\rm{ + }}{\rm{]}}}}}}\; = \;{\rm{p}}{K_{\rm{a}}}\]
This is because the concentrations of the ammonia and the ammonium ion become equal.
Notice that we are talking about the pKa of NH4+ which is the conjugate acid of ammonia and is equal to 9.25.
pH at The Equivalence Point
The equivalence point is reached when the moles of the added HCl are equal to the initial moles of the ammonia in the solution, and that corresponds to 25.0 mL of HCl. In other words, the amount of the acid was enough to neutralize all the base in the solution.
At this point, the only predominant species in the solution becomes the NH4Cl which is dissociated into NH4+ and Cl– ions. The chloride ion has no effect on the pH of the solution because it is the conjugate base of a strong acid HCl.
The pH is dictated by the hydrolysis of the ammonium ion which produces some H3O+ thus making the solution acidic, so the pH < 7 at the equivalence point.
NH4+(aq) + H2O(l) → NH3(aq) + H3O+(aq) (acidic)
To start the calculations, we need to concentration of the ammonium ion. We can calculate the moles based on the moles of 25.0 mL HCl solution:
\[{\rm{n}}\,{\rm{(N}}{{\rm{H}}_{\rm{4}}}^{\rm{ + }}{\rm{)}}\;{\rm{ = }}\,{\rm{n}}\,{\rm{(HCl)}}\;{\rm{ = }}\,{\rm{0}}{\rm{.0250}}\,\cancel{{\rm{L}}}\,{\rm{ \times }}\,\frac{{{\rm{0}}{\rm{.10}}\,{\rm{mol}}}}{{{\rm{1}}\,\cancel{{\rm{L}}}}}\,{\rm{ = }}\,{\rm{0}}{\rm{.00250}}\,{\rm{mol}}\]
The concentration would then be:
\[{\rm{M}}\,{\rm{(N}}{{\rm{H}}_{\rm{4}}}^{\rm{ + }}{\rm{)}}\;{\rm{ = }}\,\frac{{{\rm{0}}{\rm{.00250}}\,{\rm{mol}}}}{{{\rm{0}}{\rm{.0250}}\,{\rm{L}}\;{\rm{ + }}\,{\rm{0}}{\rm{.0250}}\,{\rm{L}}}}\;{\rm{ = }}\,{\rm{0}}{\rm{.0500}}\,{\rm{mol/L}}\]
From here, it is the same procedure as we do when calculating the pH of a weak acid.
Assign x mol/l for ionization and set up an ICE table to determine the [H3O+]:
-x +x +x
NH4+(aq) + H2O(l) ⇆ NH3(aq) + H3O+(aq)
|
|
[NH4+] |
[NH3] |
[H3O+] |
|
Initial |
0.0500 |
0 |
0 |
|
Change |
-x |
+x |
+x |
|
Equil |
0.0500 – x |
x |
x |
Next, write the expression for Ka using the equilibrium concentrations in the ICE table:
\[{K_{{\rm{a}}}}\; = \,\frac{{{\rm{[N}}{{\rm{H}}_{\rm{3}}}{\rm{][}}{{\rm{H}}_{\rm{3}}}{{\rm{O}}^{\rm{ + }}}{\rm{]}}}}{{{\rm{[N}}{{\rm{H}}_{\rm{4}}}^{\rm{ + }}{\rm{]}}}}\; = \;\frac{{{{\rm{x}}^{\rm{2}}}}}{{{\rm{0}}{\rm{.0500}}\,{\rm{ – }}\;{\rm{x}}}}\; \approx \;\frac{{{{\rm{x}}^{\rm{2}}}}}{{{\rm{0}}{\rm{.0500}}}} = \;{\rm{5}}{\rm{.7 x 1}}{{\rm{0}}^{{\rm{ – 10}}}}\]
Therefore, x = 5.34 x 10-6
The approximation was valid:
\[\% \, = \;\frac{{5.34\, \times \;{{10}^{ – 6}}}}{{0.0500}}\; \times \;100\% \; = \;0.0106\% \]
The concentration of H3O+ ions is 5.34 x 10-6 M, so the pH is:
pH = -log 5.34 x 10-6 = 5.28
pH After the Equivalence Point
After the equivalence point, when all the ammonia has been reacted with the acid, the only predominant species in the solution becomes the excess HCl which makes the solution very acidic, and the pH reaches up to 1.30.
This is a fairly straightforward calculation, and you check the post “pH of Strong acids and Bases” for more details.
The Weak Base – Strong Acid Titration Curve
And finally, let’s plot the data to obtain a representative graph for the titration of a weak base by a strong acid.
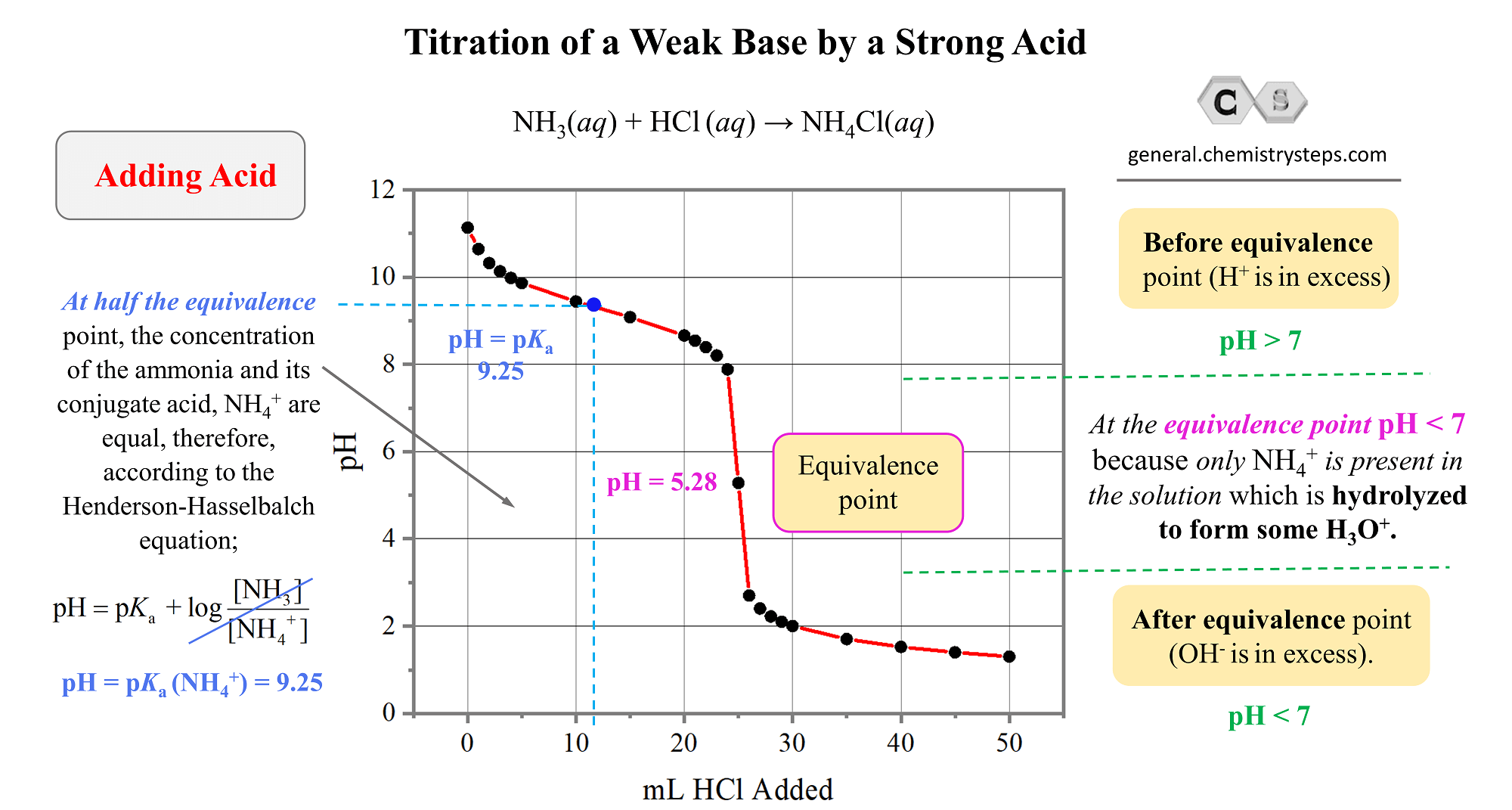
The key information and patters
- The pH starts high and goes down as the acid is added.
- The equivalence point is reached when the moles of the acid are equal to the moles of the base in the solution. That is when all the ammonia has been neutralized. What is interesting, and different from the strong acid-base titrations, is that the pH at the equivalence point is not 7. It is 5.28, and this because of the accumulated ammonium. It is a salt of a strong acid, and a weak base, therefore, it makes the solution acidic thus decreasing the pH. Go over the acid-base properties of salts, if this is still not clear.
NH4+(aq) + H2O(l) → NH3(aq) + H3O+(aq) (acidic)
Remember that in the reaction of HCl and NaOH, there was NaCl forming which is a salt of strong and a strong base, therefore has no effect on the pH.
NaOH(aq) + HCl (aq) → NaCl(aq) + H2O(l)
pH neutral salt
On the other hand, the pH at the equivalence point for the titration of a weak acid by a strong base resulted in a pH > 7. For example, in the case of acetic acid, it is due to the accumulated acetate which is a salt of a weak acid, and a strong base, therefore, it increases the pH.
CH3CO2H(aq) + OH–(aq) → CH3CO2–(aq) + H2O(l) (basic)
- At half the equivalence point, the pH is equal to the pKa of the conjugate acid of the weak base. In this case, it is the ammonium ion with pKa = 9.25.
Check Also
- Buffer Solutions
- The Henderson–Hasselbalch Equation
- The pH of a Buffer Solution
- Preparing a Buffer with a Specific pH
- The Common Ion Effect
- The pH and pKa Relationship
- Strong Acid–Strong Base Titrations
- Titration of a Weak Acid by a Strong Base
- Titration of Polyprotic Acids
- Buffer Solutions Practice Problems
- Ksp and Molar Solubility
- The Effect of a Common Ion on Solubility
- The Effect of pH on Solubility
- Will a Precipitate Form? Ksp and Q
- Ksp and Molar Solubility Practice Problems
