In the previous post, we learned how to determine whether the solution of a salt is going to be acidic or basic depending on how it was prepared.
In short, there is only one step to do this and that is finding the strong component of the salt. If the salt is made of strong acid and a weak base, then it will give an acidic solution. If it is prepared from a strong base and weak aid, the solution will be basic, and if it is a combination of a strong acid and a strong base, a neutral solution will be formed.
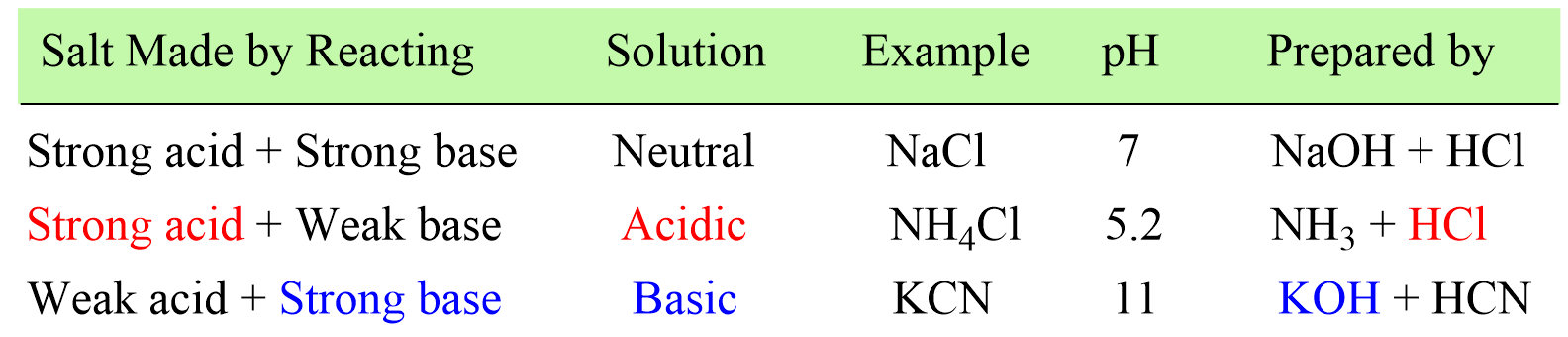
Today, we will discuss calculating the pH of a salt solution.
The pH of Salt Prepared from a Strong Acid and a Weak Base
For example, calculate the pH of 0.10 M solution of NH4Cl. Kb of NH3 is 1.76 x 10-5
Ammonium chloride (NH4Cl) is the salt of ammonia (NH3) and hydrochloric acid (HCl) and it yields an acidic solution. So, let’s follow what we have discussed earlier and see why it produces an acidic solution.
Step 1. Determine the acid and base that the salt is prepared from:
NH3 + HCl → NH4Cl
It is made of a weak base ammonia and a strong base HCl, and therefore, the solution is going to be acidic.
Step 2. Dissociate the salt and write the reaction of the weak component ion with water.
NH4Cl → NH4+ + Cl–
Step 3. Write the reaction with water.
NH4+ is the ion with a weaker component (NH3), so it is going to react with water producing hydronium ion which makes the solution acidic:
NH4+(aq) + H2O(l) → NH3(aq) + H3O+(aq) (acidic)
The next part is to determine the concentration of H3O+ ions in order to calculate the pH.
Step 4. Determine the Ka.
We are given the Kb, which measures the base strength of it and is based on the reaction of ammonia itself with water:
NH3(aq) + H2O(aq) ⇆ NH4+(aq) + OH–(aq)
This equation does not contain H+/H3O+ ions, and we do not know the concentration of ammonia, therefore, we need to determine the Ka. Ka and Kb can be calculated from one another using the relationship:
Ka · Kb = Kw = 10-14
Rearranging this, we get an expression for Ka:
\[{K_{\rm{a}}}\; = \,\frac{{{K_{\rm{w}}}}}{{{K_{\rm{b}}}}}\; = \;\frac{{{\rm{1}}{{\rm{0}}^{{\rm{ – 14}}}}}}{{{\rm{1}}{\rm{.76}}\; \times \;{\rm{1}}{{\rm{0}}^{{\rm{ – 5}}}}}}\; = \;{\rm{5}}{\rm{.7 }} \times {\rm{ 1}}{{\rm{0}}^{{\rm{ – 10}}}}\]
Step 5. Set up an ICE table to Determine the [H3O+]
Now that we know the value of Ka, we can set up an ICE table for Ka assigning x mol/l for ionization. From now on, it is the same procedure as we do when calculating the pH of a weak acid.
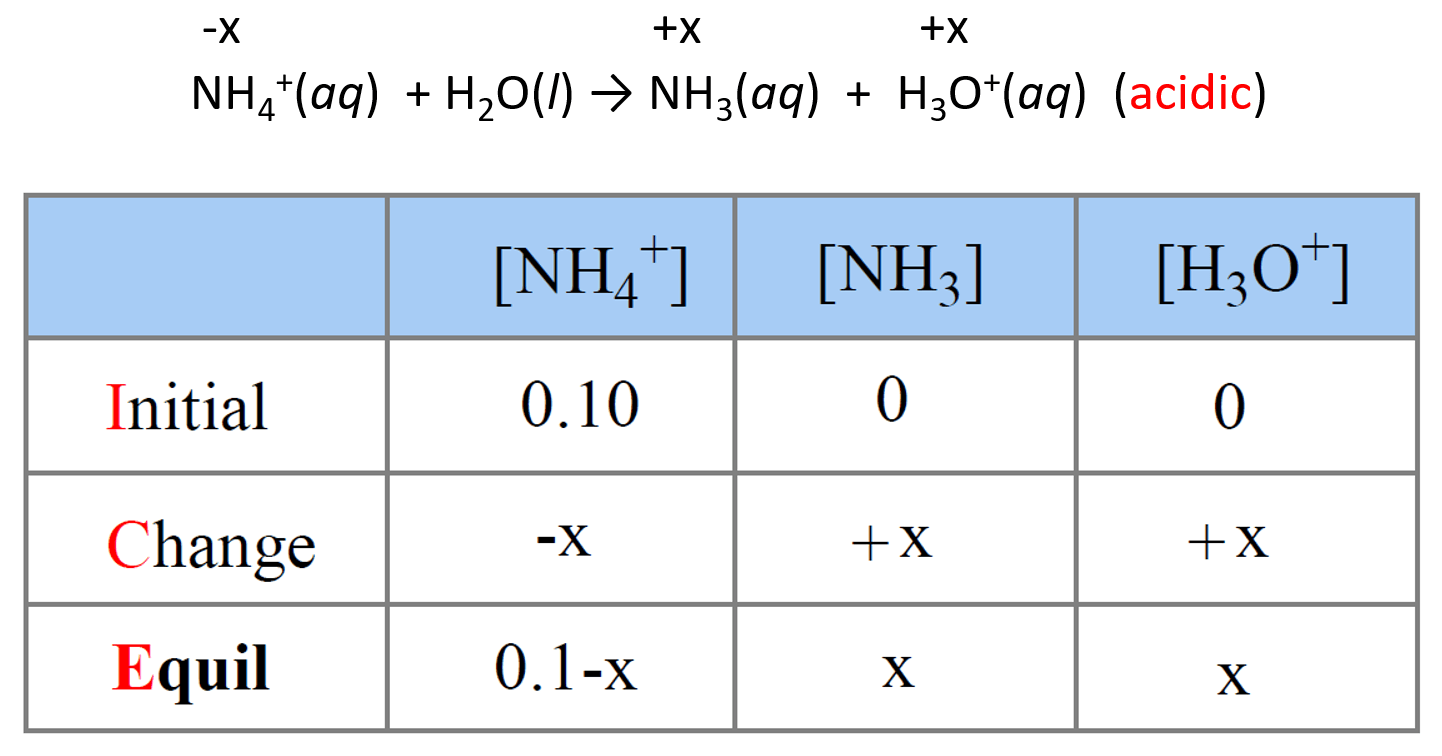
Next, write the expression for Ka using the equilibrium concentrations in the ICE table:
\[{K_{{\rm{a}}}}\; = \,\frac{{{\rm{[N}}{{\rm{H}}_{\rm{3}}}{\rm{][}}{{\rm{H}}_{\rm{3}}}{{\rm{O}}^{\rm{ + }}}{\rm{]}}}}{{{\rm{[N}}{{\rm{H}}_{\rm{4}}}^{\rm{ + }}{\rm{]}}}}\; = \;\frac{{{{\rm{x}}^{\rm{2}}}}}{{{\rm{0}}{\rm{.10}}\;{\rm{ – }}\;{\rm{x}}}}\; \approx \;\frac{{{{\rm{x}}^{\rm{2}}}}}{{{\rm{0}}{\rm{.10}}}} = \;{\rm{5}}{\rm{.7 x 1}}{{\rm{0}}^{{\rm{ – 10}}}}\]
Notice that we used an approximation that x is very small compared to the initial concentration of the salt. To check if the approximation was valid, calculate the precent ratio of x and the initial concentration:
\[\% \, = \;\frac{{7.5\, \times \;{{10}^{ – 6}}}}{{0.10}}\; \times \;100\% \; = \;0.0075\% \]
The hydrolyzation reaction percent is less than 5%, and therefore, the approximation is valid.
The concentration of H3O+, so the pH is:
pH = -log 7.5 x 10-6 = 5.1
This indicates an acidic solution which is what we expected to have for the solution of NH4Cl.
The pH of Salt Prepared from a Strong Base and a Weak Acid
For example, calculate the pH of 0.20 M solution of KCN. Ka for HCN is 4.9 x 10-10
Step 1. Determine the acid and base that the salt is prepared from.
Potassium cyanide (KCN) is prepared from a strong base (KOH) and weak acid (HCN), and therefore, its aqueous solution will be basic.
KOH + HCN → KCN + H2O
Step 2. Dissociate the salt
KCN(aq) → K+(aq) + CN–(aq)
Step 3. Write the reaction of the weak component with water.
K+ comes from a strong base KOH, so does not react with water. CN– comes from a weak acid HCN, so it will react with water.
CN–(aq) + H2O(l) → HCN(aq) + OH–(aq) (basic)
Step 4. We are given the Ka, so we need to determine the Kb.
\[{K_{\rm{b}}}\; = \,\frac{{{K_{\rm{w}}}}}{{{K_{\rm{a}}}}}\; = \;\frac{{{\rm{1}}{{\rm{0}}^{{\rm{ – 14}}}}}}{{{\rm{4}}{\rm{.9}}\; \times \;{\rm{1}}{{\rm{0}}^{{\rm{ – 10}}}}}}\; = \;{\rm{2}}{\rm{.0 }} \times {\rm{ 1}}{{\rm{0}}^{{\rm{ – 5}}}}\]
Step 5. Set up an ICE table for Kb assigning x mol/l for ionization.
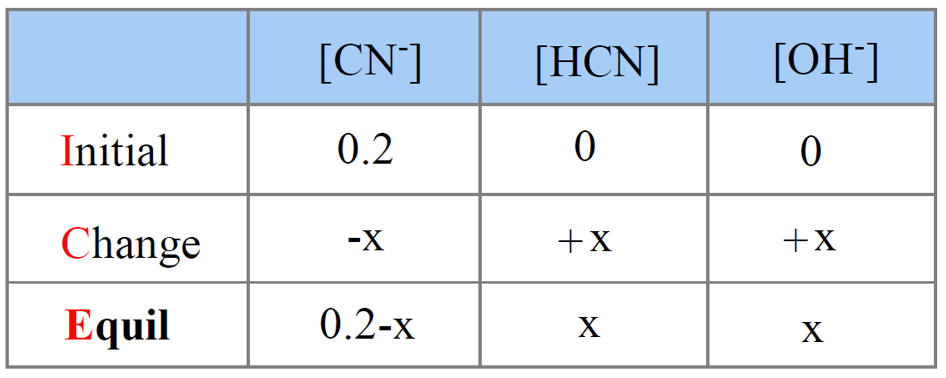
Step 6. Write the expression for Kb using the equilibrium concentration sin the ICE table in order to determine [OH–].
\[{K_{\rm{b}}}\; = \,\frac{{{\rm{[HCN][O}}{{\rm{H}}^{\rm{ – }}}{\rm{]}}}}{{{\rm{[C}}{{\rm{N}}^{\rm{ – }}}{\rm{]}}}}\; = \;\frac{{{{\rm{x}}^{\rm{2}}}}}{{{\rm{0}}{\rm{.20}}\;{\rm{ – }}\;{\rm{x}}}}\; \approx \;\frac{{{{\rm{x}}^{\rm{2}}}}}{{{\rm{0}}{\rm{.20}}\;}}\; = \;2.0\; \times \;{10^{ – 5}}\]
Solving for x, we find that x = 0.0020 mol/l and we check if the approximation was valid:
\[\% \, = \;\frac{{0.0020}}{{0.20}}\; \times \;100\% \; = \;1.0\% \]
The approximation is valid, so the concentration of OH– ions at equilibrium is 0.0020 M.
We can now calculate the pOH, and then pH using the pH + pH = 14 relationship:
pOH = -log 0.0020 = 2.7, and therefore, the pH is:
pH = 14 – pOH = 14 – 2.7 = 11.3
And this answer is also reasonable because we predicted to have a basic solution.
Salts the Yield Neutral Solutions
We have seen earlier that a salt with a cation and an anion of a strong base and a strong acid, yields a neutral solution because the ions do not react with water, and thus, no H3O+ or OH– is generated. For example, the table salt NaCl fount also in physiological solutions has a negligible effect on the pH of the solution.
In the next post, we will discuss determining the pH of a salt prepared from a weak and a weak base.
Check Also
- Definitions of Acids and Bases
- Acid-Base Reactions
- Acid-Base Titrations
- Conjugate Acid and Conjugate Base
- Autoionization of Water and Kw
- The pH and Acidity
- Acid Strength, Ka, and pKa
- Base Strength, Kb and pKb
- Ka, pKa, Kb, and pKb Relationship
- The pH of a Strong Acid and Base
- pH + pOH = 14
- The pH of a Weak Acid
- The pH of a Weak Base
- ThepH of Polyprotic Acids
- The acidity of a Salt Solution
- The pH of a Salt Solution
- The pH of Salts With Acidic Cations and Basic Anions
- Acids and Bases Practice Problems
