Polyprotic acids have more than one dissociable proton, and they dissociate in a stepwise manner. Each dissociation step is characterized by its own acid-dissociation constant, Ka1, Ka2, and so forth. For example, the carbonic acid is a weak, polyprotic acid and the dissociation constant of each step has a different value:
H2CO3(aq) + H2O(l) ⇆ HCO3–(aq) + H3O+(aq) Ka1 = 4.3 x 10-7
HCO3–(aq) + H2O(l) ⇆ CO32-(aq) + H3O+(aq) Ka2 = 5.6 x 10-11
So, when determining the pH of their solution, we need to find the total concentration of protons formed in each step. And the question is do we need to set up an ICE table for each step to determine the concentration of protons like we did for monoprotic weak acids.
Fortunately, finding the pH of a polyprotic acid solution is not as difficult because, for most polyprotic acids, Ka1 is much larger than Ka2, and Ka3 is almost neglectable compared to those.
This is because it is easier to remove a proton from a neutral acid molecule (H2CO3) rather than from a negatively charged conjugate base (HCO3–) of the acid.
Therefore, the H+/H3O+ ions generated in the second and especially the third steps are ignored when calculating the pH.
For example:
Calculate the pH of 0.10 M carbonic acid.
First, let’s write the dissociate equation of H2CO3:
H2CO3(aq) + H2O(l) ⇆ HCO3–(aq) + H3O+(aq) Ka1 = 4.3 x 10-7
(HCO3–(aq) + H2O(l) ⇆ CO32-(aq) + H3O+(aq)– ignore the second step
The initial concentration of H2CO3 is 0.10 M, and we assign x M as the concentration of H2CO3 that dissociates.
The initial concentration of H3O+ and HCO3– ions are 0, but at equilibrium, they are going to be x mol/l because that is how much the H2CO3 dissociates. The equilibrium concentration of H2CO3 is going to be decreased by x mol/l, so it is (0.10 – x) M.
Next, we set up an ICE table:
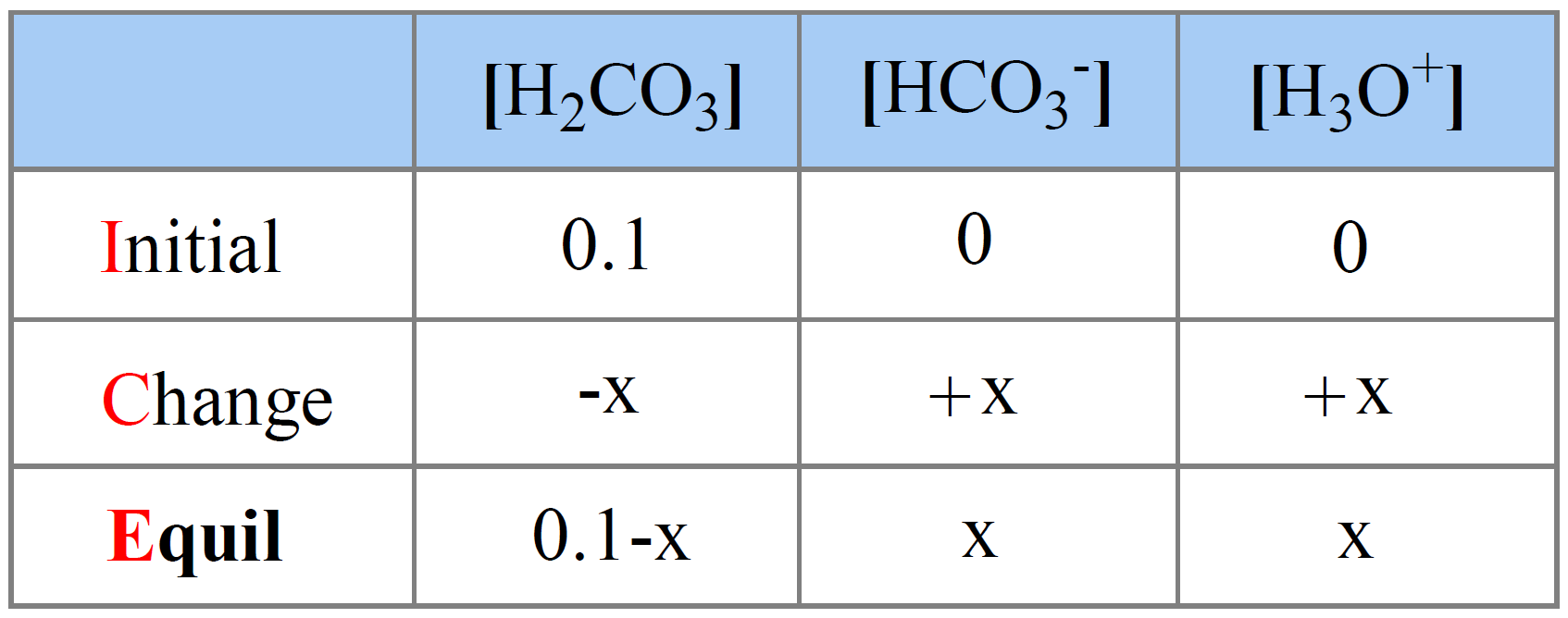
The expression for the equilibrium constant Ka is:
\[{K_{{\rm{a1}}}}\; = \,\frac{{{\rm{[HC}}{{\rm{O}}_{\rm{3}}}^{\rm{ – }}{\rm{][}}{{\rm{H}}_{\rm{3}}}{{\rm{O}}^{\rm{ + }}}{\rm{]}}}}{{{\rm{[}}{{\rm{H}}_{\rm{2}}}{\rm{C}}{{\rm{O}}_{\rm{3}}}{\rm{]}}}}\; = \;\frac{{{{\rm{x}}^{\rm{2}}}}}{{{\rm{0}}{\rm{.10}}\;{\rm{ – }}\;{\rm{x}}}}\; = \;{\rm{4}}{\rm{.3 x 1}}{{\rm{0}}^{{\rm{ – 7}}}}\]
This is a quadratic equation and remember a shorted way of solving it to use an approximation that 0.10 – -x ≈ 0.10 because, the dissociation constant is very small and therefore, the percentage of acid dissociation is negligible compared to its initial concentration.
Doing so, we get a simplified equation:
\[\;\frac{{{{\rm{x}}^{\rm{2}}}}}{{{\rm{0}}{\rm{.1}}}}\; = \;{\rm{4}}{\rm{.3 x 1}}{{\rm{0}}^{{\rm{ – 7}}}}\]
Therefore, x = 2.1 x 10-4
Make sure the approximation is valid, and for this, x must be less than 5% of H2CO3 initial concentration (less than 5% of the acid dissociates).
\[\frac{{{\rm{2}}{\rm{.1 x 1}}{{\rm{0}}^{{\rm{ – 4}}}}}}{{{\rm{0}}{\rm{.10}}\;}}\;{\rm{ \times }}\;{\rm{100\% }}\;{\rm{ = }}\;{\rm{0}}{\rm{.21\% }}\]
The approximation is valid. If it is not, you need to determine the x by solving the quadratic equation.
So, x = 4.1 x 10-5 , and this is the [H+] at equilibrium, therefore,
pH = -log 2.1 x 10-4 = 3.7
In the end, you can also plug the numbers to check if Ka1 matches the given value:
\[{K_{{\rm{a1}}}}\; = \;\frac{{{{\left( {{\rm{2}}{\rm{.1}}\; \times {\rm{1}}{{\rm{0}}^{{\rm{ – 4}}}}} \right)}^{\rm{2}}}}}{{{\rm{0}}{\rm{.1}}\;{\rm{ – }}\;{\rm{2}}{\rm{.1}}\; \times \;{\rm{1}}{{\rm{0}}^{{\rm{ – 4}}}}}}\; = \;{\rm{4}}{\rm{.4 x 1}}{{\rm{0}}^{{\rm{ – 7}}}}\]
The pH of Sulfuric Acid
H2SO4 is perhaps the only noticeable exception to ignoring the Ka2 when calculating the pH of a polyprotic acid.
It is a strong polyprotic acid and dissociates completely in the first step going from H2SO4 to HSO4– while in the second step, where the negatively charged HSO4– lose a proton and generating even more unstable SO42- ion, the acid-dissociation constant is 105 times smaller:
H2SO4(aq) + H2O(l) ⇆ HSO4–(aq) + H3O+(aq) Ka1 = 1.0 x 103
HSO4–(aq) + H2O(l) ⇆ SO42-(aq) + H3O+(aq) Ka2 = 1.2 x 10-2
Nonetheless, Ka2 is still quite a large number compared to the ones of many polyprotic acids. In addition, because in the first step the acid is completely ionized, there is a significant amount of H3O+ unlike, for example, what we have seen for carbonic acid.
For example,
Calculate the pH of 0.20 M H2SO4. Ka1 = 1.0 x 103, Ka2 = 1.2 x 10-2
There are two steps of generating H3O+ and to calculate the pH, we need to find the total concentration of hydronium ion generated in these two steps.
H2SO4(aq) + H2O(l) ⇆ HSO4–(aq) + H3O+(aq) Ka1 = 1.0 x 103
HSO4–(aq) + H2O(l) ⇆ SO42-(aq) + H3O+(aq) Ka2 = 1.2 x 10-2
Because the first ionization step is 100%, there will be 0.20 M H3O+ formed and this will be added to the [H3O+] obtained in the second step of ionization.
Now, to calculate the concentration of H3O+ formed in the second step, we need to set up an ICE table
using 0.20 M initial concentration of HSO4–, and x mol/l as the amount that is ionized to SO42-. The 0.20 M initial concentration of HSO4– comes from the complete dissociation of 0.20 M H2SO4.
The total [H3O+] at equilibrium is going to be 0.20 (from the first step of dissociation) + x (from the second step of dissociation):
0.20 0.20 0.20
H2SO4(aq) + H2O(l) ⇆ HSO4–(aq) + H3O+(aq)

\[{K_{{\rm{a2}}}}\; = \,\frac{{{\rm{[S}}{{\rm{O}}_{\rm{4}}}^{{\rm{2 – }}}{\rm{][}}{{\rm{H}}_{\rm{3}}}{{\rm{O}}^{\rm{ + }}}{\rm{]}}}}{{{\rm{[HS}}{{\rm{O}}_{\rm{4}}}^{\rm{ – }}{\rm{]}}}}\;{\rm{ = }}\;\frac{{\left( {\rm{x}} \right)\left( {{\rm{0}}{\rm{.20}}\;{\rm{ + }}\,{\rm{x}}} \right)}}{{{\rm{0}}{\rm{.20}}\;{\rm{ – }}\;{\rm{x}}}}\;{\rm{ = }}\;{\rm{1}}{\rm{.2 x 1}}{{\rm{0}}^{{\rm{ – 2}}}}\]
Ka2 is fairly large and if we neglect x compared to 0.20, we’d have Ka2 = x = 0.012. This corresponds to 6% ionization, so we cannot do that. Therefore, we need to solve the quadratic equation:
x2 + 0.212x – 0.0024 = 0
\[{\rm{x}}\;{\rm{ = }}\;\frac{{ – b \pm \sqrt {{b^2} – 4ac} }}{{2a}}\]
a = 1, b = 0.212, c = -0.0024
x = 0.011 mol/L
The total concentration of H3O+ is 0.20 + 0.011 = 0.211, therefore, the pH is:
pH = -log 0.211 = 0.68
To summarize, when calculating the pH of a polyprotic acid, in most cases, the second ionization step is ignored, and we follow the same steps as for calculating the pH of a weak monoprotic acid:
1) Write the equation for the dissociation of the acid.
2) Assign x mol/l for the concentration of the acid that dissociates.
3) Set up an ICE table.
4) Use the equilibrium concentration from the ICE table to set up an equation and solve for the x.
5) Calculate the pH based on the value of the x.
Check Also
- Definitions of Acids and Bases
- Acid-Base Reactions
- Acid-Base Titrations
- Conjugate Acid and Conjugate Base
- Autoionization of Water and Kw
- The pH and Acidity
- Acid Strength, Ka, and pKa
- Base Strength, Kb and pKb
- Ka, pKa, Kb, and pKb Relationship
- The pH of a Strong Acid and Base
- pH + pOH = 14
- The pH of a Weak Acid
- The pH of a Weak Base
- The acidity of a Salt Solution
- The pH of a Salt Solution
- The pH of Salts With Acidic Cations and Basic Anions
- Acids and Bases Practice Problems
