Titration is a common laboratory technique for determining the concentration of a solute. The most common types of titrations are acid-base titrations and redox titrations. Today’s topic is the acid-base titrations so let’s see how they work.
Before the titration begins, the solution with the known concentration, also known as the titrant, is added to the burette, and the solution with an unknown concentration, the analyte, is placed in an Erlenmeyer flask under the burette. The titrant then is added dropwise to the analyte until the acid or the base in it is neutralized.
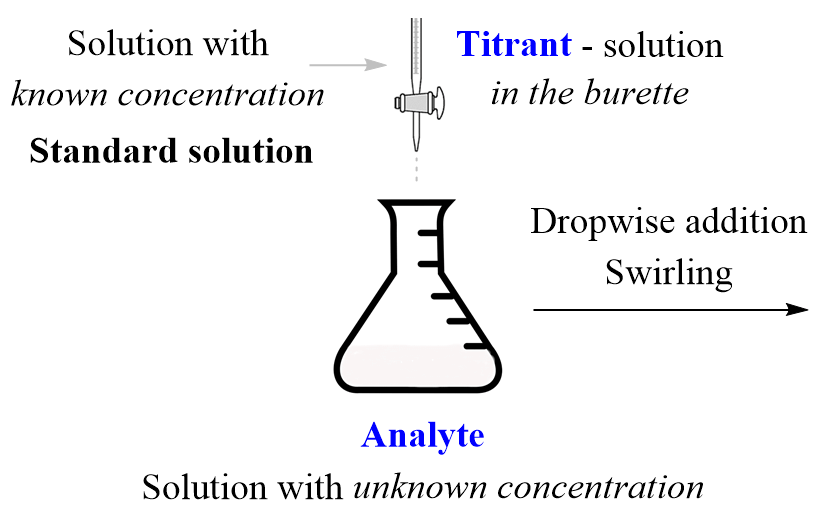
So, how do we know when it is neutralized and why do we stop at that point?
First, remember that the purpose of the titration is to demine the concentration of the unknown solution. If you wonder about it, yes, it is known as we know what is in the solution, but we don’t know the concentration, and for simplicity, we call it an unknown solution.
And the idea is this: we know the volume of the unknown solution, so if we knew the moles of the acid or the base in it, we could calculate the concentration using the formula for molarity. In general, determining the concentration or amount of the analyte by measuring volume is called volumetric analysis.
Now, the moles of the acid or the base is determined based on the stoichiometry of the acid-base reaction between the components of the standard and unknown solutions.
For example, if we want to determine the concentration of an HCl solution, we can use a standard solution of NaOH, and determine the moles of HCl using their 1 : 1 ratio:
2NaOH(aq) + HCl (aq) → NaCl(aq) + 2H2O(l)
The next question is, how do we know when to stop the titration? This should be done when there is no excess of an acid or a base left in the solution. In other words, the titration should be stopped when the concentrations of H+ and OH– ions are equal. This is the equivalence point, and it is essentially what we have in water as very little of it is dissociated and the con concentrations of H+ and OH– ions are equal (Kw – Chem II material).
To spot the equivalence point, we use an indicator which is a dye that changes its color when switching from acidic to a basic solution.
In practice though, the addition is continued slowly until the indicator signals a permanent color change, which is called the endpoint. Ideally, just one drop of addition should switch from the equivalence to the endpoint.
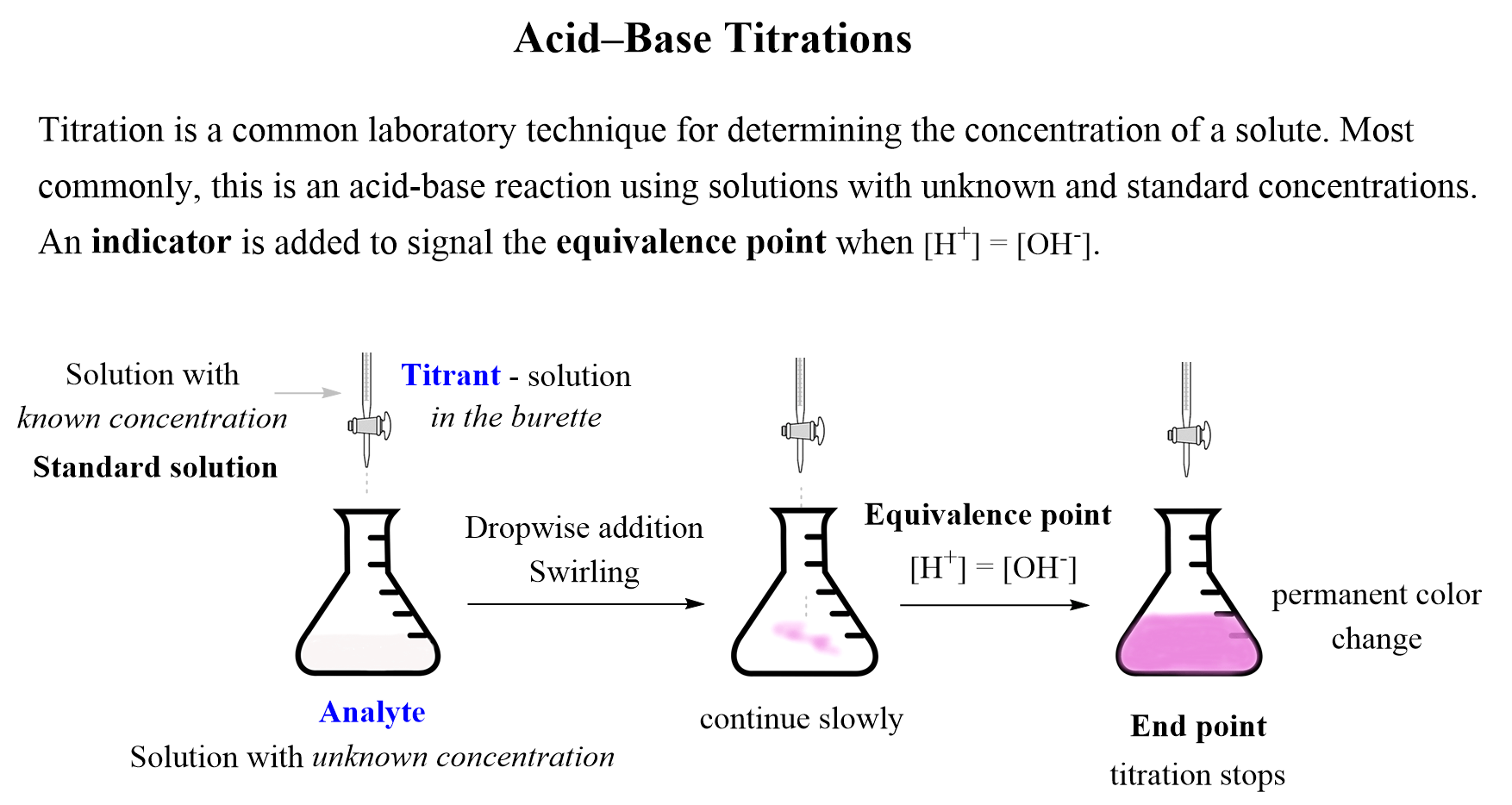
This tiny amount over the equivalence point does not affect the accuracy very much and is needed to change the solution from acidic to basic which is the reason for the color change of the indicator. A common indicator used in acid-base titrations is phenolphthalein, which is colorless in acid media, and purple when the solution becomes basic.
For example, in a titration experiment, it was determined that 45 mL of a 0.10 M NaOH solution was needed to neutralize a 20.0 mL solution of KHP. What is the molarity of the KHP solution?
KHP is the abbreviation of potassium hydrogen phthalate (KHC8H4O4) which is a monoprotic acid commonly used in acid-base titration.
The reaction can be written as:
![]()
The plan is to calculate the moles of NaOH and using the stoichiometric ratio, determine the moles of KHP. Once the moles of KHP are known, we can use it to calculate its concentration using the formula for molarity:

\[{\rm{1) n (NaOH)}}\;{\rm{ = }}\;0.045\,\cancel{{\rm{L}}}\, \times \,\frac{{{\rm{0}}{\rm{.10}}\;{\rm{mol}}}}{{{\rm{1}}\;\cancel{{\rm{L}}}}}\; = {\rm{0}}{\rm{.0045}}\;{\rm{mol}}\]
2) Because the molar ratio is 1:1, the moles of KHP reacted are also 0.0045 mol.
\[{\rm{3)}}\;{\rm{M (KHP)}}\;{\rm{ = }}\;\frac{{\rm{n}}}{{\rm{V}}}\;{\rm{ = }}\;\frac{{{\rm{0}}{\rm{.0045}}\;{\rm{mol}}}}{{{\rm{0}}{\rm{.0200}}\;{\rm{L}}}}\; = {\rm{0}}{\rm{.225}}\;{\rm{mol/L}}\]
The neutralization reaction between NaOH and KHP simplifies the calculations because of the 1:1 molar ratio. Let’s do another example, where a diprotic acid H2SO4 is used instead of KHP.
How many milliliters (mL) of a 0.85 M NaOH solution are needed to neutralize 135 mL of a 0.260 M H2SO4 solution?
First, write the acid-base reaction:
2NaOH(aq) + H2SO4 (aq) → Na2SO4 (aq) + 2H2O(l)
The plan is still the same, and we need to determine the moles of H2SO4 first. Make sure to convert the mL to L because the units of molarity are mol/L.
\[\begin{array}{l}{\rm{V(}}{{\rm{H}}_{\rm{2}}}{\rm{S}}{{\rm{O}}_{\rm{4}}}{\rm{)}}\;{\rm{ = }}\;{\rm{135}}\;{\rm{mL}}\,{\rm{ \times }}\,\frac{{{\rm{1}}\;{\rm{L}}}}{{{\rm{1000}}\;{\rm{mL}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.135}}\;{\rm{L}}\\\end{array}\]
\[{\rm{n}}\;{\rm{(}}{{\rm{H}}_{\rm{2}}}{\rm{S}}{{\rm{O}}_{\rm{4}}}{\rm{)}}\;{\rm{ = }}\;{\rm{M}}\,{\rm{ \times }}\,{\rm{V}}\;{\rm{ = }}\,{\rm{0}}{\rm{.260}}\;\frac{{{\rm{mol}}}}{{\rm{L}}}\,{\rm{ \times }}\;{\rm{0}}{\rm{.135}}\;{\rm{L}}\;{\rm{ = }}\;{\rm{0}}{\rm{.0351}}\;{\rm{mol}}\]
Next, use the molar ratio to determine the moles of NaOH:
\[{\rm{n}}\;{\rm{(NaOH)}}\;{\rm{ = }}\;{\rm{0}}{\rm{.0351}}\;\cancel{{{\rm{mol}}\,{{\rm{H}}_{\rm{2}}}{\rm{S}}{{\rm{O}}_{\rm{4}}}}}\;{\rm{ \times }}\,\frac{{{\rm{2}}\;{\rm{mol}}\,{\rm{NaOH}}}}{{{\rm{1}}\,\cancel{{{\rm{mol}}\,{{\rm{H}}_{\rm{2}}}{\rm{S}}{{\rm{O}}_{\rm{4}}}}}}}\;{\rm{ = }}\;{\rm{0}}{\rm{.0702}}\,{\rm{mol}}\]
And finally, the volume of NaOH solution is determined using the molarity formula:
\[{\rm{3)}}\;{\rm{V}}\;{\rm{ = }}\;\frac{{\rm{n}}}{{\rm{M}}}\;{\rm{ = }}\;\frac{{{\rm{0}}{\rm{.0702}}\;{\rm{mol}}}}{{{\rm{0}}{\rm{.85}}\;{\rm{mol/L}}}}\;{\rm{ = 0}}{\rm{.0826}}\;{\rm{L}}\;{\rm{ = }}\;{\rm{82}}{\rm{.6}}\;{\rm{mL}}\]
There is a lot more to acid-base titrations, in particular, the pH change during the experiment demonstrated by titration curves. These are usually covered in chem 2 curriculum, but I will leave the links here in case you need them:
- Strong Acid–Strong Base Titrations
- Titration of a Weak Acid by a Strong Base
- Titration of a Weak Base by a Strong Acid
- Titration of Polyprotic Acids
Check Also
- Solutions
- Strong and Weak Electrolytes
- Dissociation of Ionic Compounds
- Molecular, Ionic, and Net Ionic Equations
- Molarity
- Dilution
- Ion Concentration
- Precipitation Reactions
- Definitions of Acids and Bases
- Acid-Base Reactions
- Stoichiometry of Reactions in Aqueous Solutions
- Oxidation State
- Oxidation-Reduction (Redox) Reactions
- Reactions in Aqueous Solutions Practice Problems
Practice
27.0 mL of a NaOH solution was needed to neutralize 0.326 g of KHP (KHC8H4O4). What is the molarity of the NaOH solution?
What volume of 0.150 M calcium hydroxide is required to neutralize 250.0 mL of 0.0350 M sulfuric acid?
How many mL of 0.250 M HCl will neutralize 60.00 mL of 0.060 M Ba(OH)2?
A 4.598-g sample of acetylsalicylic acid (the active ingredient in aspirin) was dissolved in water. It took 35.6 mL of a 0.717 M NaOH solution to neutralize the acid. Determine the molar mass of the acid considering that it is a monoprotic acid.
