Reactions in Aqueous Solutions

Balancing Redox Reactions

Redox reactions can be balanced with the half-reaction method. The half-reaction shows the oxidation and reduction processes separately.

For example,

Zn + Ag⁺ → Zn²⁺ + Ag

Follow these steps to balance this reaction:

1) Add the oxidation states and write the half-reactions. The oxidations states are only added to help identify the oxidation and reduction processes:

2) Balance the elements. In this case, they are balanced, so proceed to the next step.

3) Balance the charges by adding electrons:

Zn → Zn²⁺ + 2e^–1e^– + Ag⁺ → Ag

4) Balance the number of electrons by multiplying the equation(s) with a whole number. The first equation has two electrons, and therefore, we multiply the second equation by two:

2 x [1e^– + Ag⁺ → Ag] = 2e^– + 2Ag⁺ → 2Ag

5) Once everything is balanced, add the half-reactions together and check if all the atoms and charges are balanced again.

Zn → Zn²⁺ + 2e^–2e^– + 2Ag⁺ → 2Ag
__________________

Zn + 2e^– + 2Ag⁺ → 2Ag + Zn²⁺ + 2e^–

6) Cancel any species that appear in equal quantitates on both sides of the equation:

Zn + 2e^– + 2Ag⁺ → 2Ag + Zn²⁺ + 2e^–

Zn + 2Ag⁺ → 2Ag + Zn²⁺

Balancing Redox Equations in Acidic Solution

In the example above, there are only two elements which simplifies balancing the reaction. There is an additional part to balancing redox reactions in acidic or basic conditions which results from the presence of oxygen and hydrogen atoms.

For example,

Fe²⁺ + Cr₂O₇^2-→ Fe³⁺ + Cr³⁺

Do as we did in the previous example;

1) Add the oxidation states and write the half-reactions:

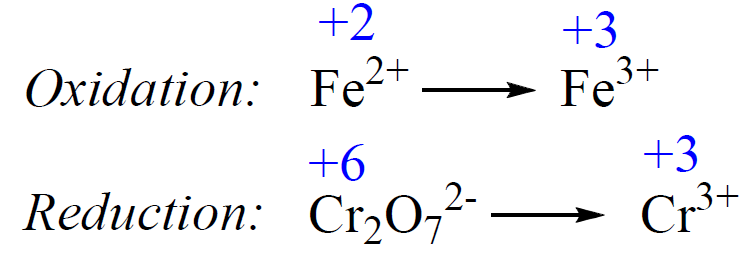
2) Balance the atoms. Add H₂O to balance the O atoms, and H⁺ to balance the H atoms.

The atoms in the first half-reaction are balanced. For the second reaction, we need to equalize the Cr atoms, and add 7 H₂O on the right side to balance the oxygen atoms:

Cr₂O₇^2-→ 2Cr³⁺+ 7H₂O

Now, to balance the H atoms, we need to add 14 H⁺ on the left side:

14H⁺ + Cr₂O₇^2-→ 2Cr³⁺+ 7H₂O

3) Balance the charges by adding electrons.

In the first equation, we add one electron on the right side:

Fe²⁺ → Fe³⁺+ 1e^–

In the second equation the charge is zero on the left side (+14 + (-7 x 2) = 0), we have +6 (+3 x 2) on the right side:

14H⁺ + Cr₂O₇^2-→ 2Cr³⁺+ 7H₂O

Therefore, add 6e^–to balance the charges in the second equation:

6e^–+ 14H⁺ + Cr₂O₇^2-→ 2Cr³⁺+ 7H₂O

4) Balance the number of electrons by multiplying the equation(s) with a whole number. There are 6 e^– in the second equation, so multiply the first equation by 6:

6 x [Fe²⁺ → Fe³⁺+ 1e^–] = 6Fe²⁺ → 6Fe³⁺+ 6e^–

5) Once everything is balanced, add the half-reactions together and cancel the electrons:

6Fe²⁺ → 6Fe³⁺+ 6e^–6e^– + 14H⁺ + Cr₂O₇^2-→ 2Cr³⁺+ 7H₂O
______________________________

6Fe²⁺+ 14H⁺ + Cr₂O₇^2-→ 6Fe³⁺+ 2Cr³⁺+ 7H₂O

Check if everything is balanced. In this case, it is!

Balancing Redox Equations in Basic Solution

For reactions in basic solutions, we proceed all the way to balancing the equation as if it is in an acidic solution. At the end, for every H+, we add an equal number of OH^– on both sides of the equation. A pair of H⁺ and OH^– ions is then represented as a water molecule.

For example,

MnO₄^– + I^–→MnO₂ + I₂

1) Write the half-reactions:

MnO₄^– → MnO₂I^– → I₂

2) Balance the atoms. Add H₂O to balance the O atoms, and H⁺ to balance the H atoms.

The atoms in the first half-reaction are balanced.

For the first reaction, we need to equalize the oxygens, and therefore, we add 2 H₂O on the right side:

MnO₄^– → MnO₂+ 2H₂O

And now, add 4 H+ on the left side to balance the hydrogens:

4H⁺+ MnO₄^– → MnO₂+ 2H₂O

For the second reaction, add 2 in front of I^–:

2I^– → I₂

3) Balance the charges by adding electrons.

To balance the charges in the first equation, we add 3e^– on the left side because there are three extra positive charges (+4 from the protons and -1 from the permanganate ion):

3e^–+ 4H⁺+ MnO₄^– → MnO₂+ 2H₂O

For the second equation, we need to add 2e^–on the right side:

2I^– → I₂+ 2e^–

4) Balance the number of electrons by multiplying the equation with whole numbers. There are 3 electrons in the first equation, and 2 electrons in the second, so ta balance this, we multiply the first equation by 2, and the second equation by 3:

2 x [3e^–+ 4H⁺+ MnO₄^– → MnO₂+ 2H₂O] = 6e^–+ 8H⁺+ 2MnO₄^– → 2MnO₂+ 4H₂O

3 x [2I^– → I₂+ 2e^–] = 6I^– → 3I₂+ 6e^–

5) Once everything is balanced, add the half-reactions together and cancel the electrons:

6e^– + 8H⁺+ 2MnO₄^– → 2MnO₂+ 4H₂O

6I^– → 3I₂+ 6e^–

^{__________________________________________________}

8H⁺+ 2MnO₄^–+ 6I^– → 2MnO₂+ 4H₂O + 3I₂

6) This is the balanced equation in acidic media, and one more step to make it in a basic media, is to add 8 OH^– on both sides of the equation to get rid of the 8H⁺ ions on the left side. This works on the principle of combining H⁺ and OH^– ions and representing it as water:

8OH^– + 8H⁺+ 2MnO₄^–+ 6I^– → 2MnO₂+ 4H₂O + 3I₂+ 8OH^–

8H₂O + 2MnO₄^–+ 6I^– → 2MnO₂+ 4H₂O + 3I₂+ 8OH^–

Notice that we now have 8 H₂O on the left side, and only for on the right side. 4 H₂O molecules on both sides cancel out, and we are left with the balanced equation in a basic media:

2MnO₄^–+ 6I^– + 4H₂O → 2MnO₂+ 3I₂+ 8OH^–

To summarize the balancing of redox reactions, remember that:

1) For reactions with only two elements, balance the atoms and then the charges by adding electrons where needed. Once the half-reactions are balanced, add them up and cancel any identical species that appear on both sides of the equation.

2) Balancing redox reactions in acidic media: Follow the same steps and remember, we add H₂O to balance the O atoms, and H⁺ to balance the H atoms.

3) Balancing redox reactions in basic media: Follow the same steps as far balancing in acidic media and, in the end, add as many OH- ions as there are on either side of the equation. Convert an equal number of these ions to water, and cancel the water molecules on both sides of the equation.

Check Also

Practice

Balance the following redox reactions occurring in acidic aqueous solution:

a) Al(s) + Fe²⁺(aq) → Al³⁺(aq) + Fe(s)

b) SO₃²^–(aq) + MnO₄^–(aq) → SO₄²^–(aq) + Mn²⁺(aq)

c) Cr₂O₇^2- + C₂O₂^2- → Cr³⁺ + CO₂

d) PbO₂ + Mn²⁺ + SO₄²^– → PbSO₄ + MnO₄^–

e) MnO₄⁻(aq) + H₂O₂(aq) → Mn²⁺(aq) + O₂(g)

answer

2Al(s) + 3Fe²⁺(aq) → 2Al³⁺(aq) + 3Fe(s)

answer

5SO₃²^–(aq) + 2MnO₄^–(aq) + 6H⁺(aq) → 5SO₄²^–(aq) + 2Mn²⁺(aq) + 3H₂O(l)

answer

3C₂O₂^2-+ Cr₂O₇^2-+ 14H⁺(aq) → 6CO₂+ 2Cr³⁺ + 7H₂O(l)

answer

2Mn²⁺ + 5PbO₂ + 5SO₄²^–+ 4H⁺(aq) → 2MnO₄^–+ 5PbSO₄+ 2H₂O(l)

answer

5H₂O₂(aq) + 2MnO₄⁻(aq) + 6H⁺(aq) → 5O₂(g) + 2Mn²⁺(aq) + 8H₂O(l)

Solution

a) Al(s) + Fe²⁺(aq) → Al³⁺(aq) + Fe(s)

1) Separate the half-reactions:

Al(s) → Al³⁺(aq) (oxidation)

Fe²⁺(aq) → Fe(s) (reduction)

2) Balance the elements. In this case, they are balanced, so proceed to the next step.

3) Balance the charges by adding electrons:

Al(s) → Al³⁺(aq) + 3e^–

Fe²⁺(aq) + 2e^–→ Fe(s)

4) Balance the number of electrons by multiplying the equation(s) with a whole number.

2Al(s) → 2Al³⁺(aq) + 6e^–

3Fe²⁺(aq) + 6e^–→ 3Fe(s)

5) Once everything is balanced, add the half-reactions together and check if all the atoms and charges are balanced again.

2Al(s) → 2Al³⁺(aq) + 6e^–

3Fe²⁺(aq) + 6e^–→ 3Fe(s)
_____________________

2Al(s) + 3Fe²⁺(aq) + 6e^–→ 2Al³⁺(aq) + 6e^–+ 3Fe(s)

6) Cancel any species that appear in equal quantitates on both sides of the equation:

2Al(s) + 3Fe²⁺(aq) + 6e^– → 2Al³⁺(aq) + 6e^– + 3Fe(s)

2Al(s) + 3Fe²⁺(aq) → 2Al³⁺(aq) + 3Fe(s)

b) SO₃²^–(aq) + MnO₄^–(aq) → SO₄²^–(aq) + Mn²⁺(aq)

1) Separate the half-reactions:

SO₃²^–(aq) → SO₄²^–(aq)

MnO₄^–(aq) → Mn²⁺(aq)

2) Balance the elements. Add H₂O to balance the O atoms, and H+ to balance the H atoms.

H₂O(l) + SO₃²^–(aq) → SO₄²^–(aq) + 2H⁺(aq)

MnO₄^–(aq) + 8H⁺(aq) → Mn²⁺(aq) + 4H₂O(l)

3) Balance the charges by adding electrons:

H₂O(l) + SO₃²^–(aq) → SO₄²^–(aq) + 2H⁺(aq) + 2e^–

MnO₄^–(aq) + 8H⁺(aq) + 5e^– → Mn²⁺(aq) + 2H₂O(l)

4) Balance the number of electrons by multiplying the equation(s) with a whole number.

5H₂O + 5SO₃²^–(aq) → 5SO₄²^–(aq) + 10H⁺(aq) + 10e^–

2MnO₄^–(aq) + 16H⁺(aq) + 10e- → 2Mn²⁺(aq) + 4H₂O(l)

5) Once everything is balanced, add the half-reactions together and check if all the atoms and charges are balanced again.

5H₂O + 5SO₃²^–(aq) → 5SO₄²^–(aq) + 10H⁺(aq) + 10e^–

2MnO₄^–(aq) + 16H⁺(aq) + 10e^– → 2Mn²⁺(aq) + 8H₂O(l)
______________________________________________

5H₂O + 5SO₃²^–(aq) + 2MnO₄^–(aq) + 16H⁺(aq) + 10e^–→ 5SO₄²^–(aq) + 10H⁺(aq) + 10e^–+ 2Mn²⁺(aq) + 8H₂O(l)

6) Cancel any species that appear in equal quantitates on both sides of the equation:

5H₂O(l) + 5SO₃²^–(aq) + 2MnO₄^–(aq) + 16 6H⁺(aq) + 10e^– → 5SO₄²^–(aq) + 10H⁺(aq) + 10e^– + 2Mn²⁺(aq) + 8 3H₂O(l)

5SO₃²^–(aq) + 2MnO₄^–(aq) + 6H⁺(aq) → 5SO₄²^–(aq) + 2Mn²⁺(aq) + 3H₂O(l)

We can rearrange the positions of species just to make the equation look a more conventional way:

2MnO₄^–(aq) + 5SO₃²^–(aq) + 6H⁺(aq) → 2Mn²⁺(aq) + 5SO₄²^–(aq) + 3H₂O(l)

c) Cr₂O₇^2- + C₂O₂^2- → Cr³⁺ + CO₂

1) Separate the half-reactions:

Cr₂O₇^2- → Cr³⁺

C₂O₂^2- → CO₂

2) Balance the elements. Add H₂O to balance the O atoms, and H+ to balance the H atoms.

Cr₂O₇^2-+ 14H⁺(aq) → 2Cr³⁺ + 7H₂O

C₂O₂^2- → 2CO₂

3) Balance the charges by adding electrons. We need 6e^– on the left side of the first equation because the charges are +12 vs +6. The second equation needs two electrons on the right side to make the charges -2 on both sides:

Cr₂O₇^2-+ 14H⁺(aq) + 6e^– → 2Cr³⁺ + 7H₂O(l)

C₂O₂^2- → 2CO₂ + 2e^–

4) Balance the number of electrons by multiplying the equation(s) with a whole number.

Cr₂O₇^2-+ 14H⁺(aq) + 6e^– → 2Cr³⁺ + 7H₂O(l)

3C₂O₂^2- → 6CO₂ + 6e^–

5) Once everything is balanced, add the half-reactions together and check if all the atoms and charges are balanced again.

Cr₂O₇^2-+ 14H⁺(aq) + 6e^– → 2Cr³⁺ + 7H₂O(l)

3C₂O₂^2- → 6CO₂ + 6e^–______________________________________________

Cr₂O₇^2-+ 14H⁺(aq) + 6e^– + 3C₂O₂^2- → 2Cr³⁺ + 7H₂O + 6CO₂ + 6e^–

6) Cancel any species that appear in equal quantitates on both sides of the equation:

Cr₂O₇^2-+ 14H⁺(aq) + 6e^– + 3C₂O₂^2- → 2Cr³⁺ + 7H₂O(l) + 6CO₂ + 6e^–

3C₂O₂^2-+ Cr₂O₇^2-+ 14H⁺(aq) → 6CO₂+ 2Cr³⁺ + 7H₂O(l)

d) PbO₂ + Mn²⁺ + SO₄²^– → PbSO₄ + MnO₄^–

1) Separate the half-reactions:

Mn²⁺ → MnO₄^–

PbO₂ + SO₄²^– → PbSO₄

2) Balance the elements. Add H₂O to balance the O atoms, and H+ to balance the H atoms.

Mn²⁺ + 4H₂O(l) → MnO₄^–+ 8H⁺(aq)

PbO₂ + SO₄²^– + 4H⁺(aq) → PbSO₄+ 2H₂O(l)

3) Balance the charges by adding electrons.

Mn²⁺ + 4H₂O(l) → MnO₄^–+ 8H⁺(aq) + 5e^–

PbO₂ + SO₄²^– + 4H⁺(aq) + 2e^–→ PbSO₄+ 2H₂O(l)

4) Balance the number of electrons by multiplying the equation(s) with a whole number. We need to multiply the first half-reaction (oxidation half-reaction) by 2 and the reduction half-reaction by 5:

2Mn²⁺ + 8H₂O → 2MnO₄^–+ 16H⁺(aq) + 10e^–

5PbO₂ + 5SO₄²^– + 20H⁺(aq) + 10e^–→ 5PbSO₄+ 10H₂O(l)

5) Once everything is balanced, add the half-reactions together and check if all the atoms and charges are balanced again.

2Mn²⁺ + 8H₂O → 2MnO₄^–+ 16H⁺(aq) + 10e^–

5PbO₂ + 5SO₄²^– + 20H⁺(aq) + 10e^–→ 5PbSO₄+ 10H₂O(l)
______________________________________________

2Mn²⁺ + 8H₂O(l) + 5PbO₂ + 5SO₄²^– + 20 4H⁺(aq) + 10e^– → 2MnO₄^–+ 16H⁺(aq) + 10e^– + 5PbSO₄+ 10 2H₂O(l)

2Mn²⁺ + 5PbO₂ + 5SO₄²^–+ 4H⁺(aq) → 2MnO₄^–+ 5PbSO₄+ 2H₂O(l)

e) MnO₄⁻(aq) + H₂O₂(aq) → Mn²⁺(aq) + O₂(g)

1) Separate the half-reactions:

H₂O₂(aq) → O₂(g)

MnO₄⁻(aq) → Mn²⁺(aq)

2) Balance the elements. Add H₂O to balance the O atoms, and H+ to balance the H atoms.

H₂O₂(aq) → O₂(g) + 2H⁺(aq)

MnO₄⁻(aq) + 8H⁺(aq) + 5e^–→ Mn²⁺(aq) + 4H₂O(l)

3) Balance the charges by adding electrons. The first reaction needs two electrons on the right, and for the second, we need 5 electrons on the left side:

H₂O₂(aq) → O₂(g) + 2H⁺(aq) + 2e^–

MnO₄⁻(aq) + 8H⁺(aq) + 5e^–→ Mn²⁺(aq) + 4H₂O(l)

4) Balance the number of electrons by multiplying the equation(s) with a whole number.

5H₂O₂(aq) → 5O₂(g) + 10H⁺(aq) + 10e^–

2MnO₄⁻(aq) + 16H⁺(aq) + 10e^–→ 2Mn²⁺(aq) + 8H₂O(l)

5) Once everything is balanced, add the half-reactions together and check if all the atoms and charges are balanced again.

5H₂O₂(aq) → 5O₂(g) + 10H⁺(aq) + 10e^–

2MnO₄⁻(aq) + 16H⁺(aq) + 10e^–→ 2Mn²⁺(aq) + 8H₂O(l)
_____________________________________________

5H₂O₂(aq) + 2MnO₄⁻(aq) + 16 6H⁺(aq) + 10e^– → 5O₂(g) + 10H⁺(aq) + 10e^– + 2Mn²⁺(aq) + 8H₂O(l)

5H₂O₂(aq) + 2MnO₄⁻(aq) + 6H⁺(aq) → 5O₂(g) + 2Mn²⁺(aq) + 8H₂O(l)

Balance the following redox reactions occurring in basic aqueous solution:

a) Mn²⁺ + ClO₃^– → MnO₂ + ClO₂

b) MnO₄^–(aq) + Br^–(aq) → MnO₂ + BrO₃^–(aq)

c) MnO₄^–(aq) + CN^–(aq) → CNO-(aq) + MnO₂(s)

d) H₂O₂(aq) + ClO₂(aq) → ClO₂^–(aq) + O₂(g)

e) MnO₄^–(aq) + Fe(OH)₂(s) → MnO₂(s) + Fe(OH)₃(s)

answer

Mn²⁺ + ClO₃^– → MnO₂ + ClO₂

answer

Br^–(aq) + 2MnO₄^–(aq) → BrO₃^–(aq) + 2MnO₂ + 2OH^–(aq)

answer

3CN^–(aq) + 2MnO₄^–(aq) + H₂O(l) → 3CNO^–(aq) + 2MnO₂(s) + 2OH^–(aq)

answer

H₂O₂(aq) + 2ClO₂(aq) + 2OH^–(aq) → O₂(g) + 2ClO₂^–(aq) + 2H₂O(l)

answer

MnO₄^–(aq) + 3Fe(OH)₂(s) + 2H₂O(l) → MnO₂(s) + 3Fe(OH)₃(s) + OH^–(aq)

Solution

a) Mn²⁺ + ClO₃^– → MnO₂ + ClO₂

1) Separate the half-reactions:

Mn²⁺ → MnO₂

ClO₃^– → ClO₂

2) Balance the elements. Add H₂O to balance the O atoms, and H+ to balance the H atoms.

Mn²⁺ + 2H₂O → MnO₂ + 4H⁺(aq)

ClO₃^– + 2H⁺(aq) → ClO₂+ H₂O(l)

3) Balance the charges by adding electrons.

Mn²⁺ + 2H₂O → MnO₂ + 4H⁺(aq) + 2e^–

ClO₃^– + 2H⁺(aq) + e^–→ ClO₂+ H₂O(l)

4) Balance the number of electrons by multiplying the equation(s) with a whole number.

Mn²⁺ + 2H₂O → MnO₂ + 4H⁺(aq) + 2e^–

2ClO₃^– + 4H⁺(aq) + 2e^–→ 2ClO₂+ 2H₂O(l)

5) Once everything is balanced, add the half-reactions together and check if all the atoms and charges are balanced again.

Mn²⁺ + 2H₂O → MnO₂ + 4H⁺(aq) + 2e^–

2ClO₃^– + 4H⁺(aq) + 2e^–→ 2ClO₂+ 2H₂O(l)
_____________________________________________

Mn²⁺ + 2H₂O + 2ClO₃^– + 4H⁺ + 2e^– → MnO₂ + 4H⁺ + 2e^– + 2ClO₂+ 2H₂O

Mn²⁺ + ClO₃^– → MnO₂ + ClO₂

We don’t need to add any OH^– ions on any side of the equation, since there are no H⁺ ions. Therefore, for this reaction, the balanced equation in basic and acidic solutions is identical.

b) MnO₄^–(aq) + Br^–(aq) → MnO₂ + BrO₃^–(aq)

1) Separate the half-reactions:

Br^–(aq) → BrO₃^–(aq)

MnO₄^–(aq) → MnO₂

2) Balance the elements. Add H₂O to balance the O atoms, and H+ to balance the H atoms.

Br^–(aq) + 3H₂O(l) → BrO₃^–(aq) + 6H⁺(aq)

MnO₄^–(aq) + 4H⁺(aq) → MnO₂ + 2H₂O(l)

3) Balance the charges by adding electrons.

Br^–(aq) + 3H₂O(l) → BrO₃^–(aq) + 6H⁺(aq) + 6e^–

MnO₄^–(aq) + 4H⁺(aq) + 3e^–→ MnO₂ + 2H₂O(l)

4) Balance the number of electrons by multiplying the equation(s) with a whole number.

Br^–(aq) + 3H₂O(l) → BrO₃^–(aq) + 6H⁺(aq) + 6e^–

2MnO₄^–(aq) + 8H⁺(aq) + 6e^–→ 2MnO₂ + 4H₂O(l)

5) Once everything is balanced, add the half-reactions together and check if all the atoms and charges are balanced again.

Br^–(aq) + 3H₂O(l) → BrO₃^–(aq) + 6H⁺(aq) + 6e^–

2MnO₄^–(aq) + 8H⁺(aq) + 6e^–→ 2MnO₂ + 4H₂O(l)
_____________________________________________

Br^–(aq) + 3H₂O + 2MnO₄^–(aq) + 8 2H⁺+ 6e^–→ BrO₃^–(aq) + 6H⁺ + 6e^– + 2MnO₂ + 4H₂O(l)

Br^–(aq) + 2MnO₄^–(aq) + 2H⁺(aq) → BrO₃^–(aq) + 2MnO₂ + H₂O(l)

6) This is the balanced red-ox reaction in acidic media, so to obtain the one in a basic solution, we need to add 2OH^– on both sides of the equation:

Br^–(aq) + 2MnO₄^–(aq) + 2H⁺(aq) + 2OH^–(aq) → BrO₃^–(aq) + 2MnO₂ + H₂O(l) + 2OH^–(aq)

The two H⁺ and OH^– ions are written as two water molecules, and one of them is canceled with the one on the right side:

Br^–(aq) + 2MnO₄^–(aq) + 2H₂O(l) → BrO₃^–(aq) + 2MnO₂ + H₂O(l) + 2OH^–(aq)

Br^–(aq) + 2MnO₄^–(aq) → BrO₃^–(aq) + 2MnO₂ + 2OH^–(aq)

c) MnO₄^–(aq) + CN^–(aq) → CNO-(aq) + MnO₂(s)

1) Separate the half-reactions:

CN^–(aq) → CNO^–(aq)

MnO₄^–(aq) → MnO₂(s)

2) Balance the elements. Add H₂O to balance the O atoms, and H+ to balance the H atoms.

CN^–(aq) + H₂O(l) → CNO^–(aq) + 2H⁺(aq)

MnO₄^–(aq) + 4H⁺(aq) → MnO₂(s) + 2H₂O(l)

3) Balance the charges by adding electrons.

CN^–(aq) + H₂O(l) → CNO^–(aq) + 2H⁺(aq) + 2e^–

MnO₄^–(aq) + 4H⁺(aq) + 3e^–→ MnO₂(s) + 2H₂O(l)

4) Balance the number of electrons by multiplying the equation(s) with a whole number.

3CN^–(aq) + 3H₂O(l) → 3CNO^–(aq) + 6H⁺(aq) + 6e^–

2MnO₄^–(aq) + 8H⁺(aq) + 6e^–→ 2MnO₂(s) + 4H₂O(l)

5) Once everything is balanced, add the half-reactions together and check if all the atoms and charges are balanced again.

3CN^–(aq) + 3H₂O(l) → 3CNO^–(aq) + 6H⁺+ 6e^–

2MnO₄^–(aq) + 8H⁺(aq) + 6e^–→ 2MnO₂(s) + 4H₂O(l)
_______________________________________

3CN^–(aq) + 3H₂O(l) + 2MnO₄^–(aq) + 8 2H⁺(aq) + 6e^– → 3CNO^–(aq) + 6H⁺ + 6e^– + 2MnO₂(s) + 4H₂O(l)

3CN^–(aq) + 2MnO₄^–(aq) + 2H⁺(aq) → 3CNO^–(aq) + 2MnO₂(s) + H₂O(l)

6) This is the balanced red-ox reaction in acidic media, so to obtain the one in a basic solution, we need to add 2OH^– on both sides of the equation:

3CN^–(aq) + 2MnO₄^–(aq) + 2H⁺(aq) + 2OH^–(aq) → 3CNO^–(aq) + 2MnO₂(s) + H₂O(l) + 2OH^–(aq)

The two H⁺ and OH^– ions are written as two water molecules, and one of them is canceled with the one on the right side:

3CN^–(aq) + 2MnO₄^–(aq) + 2H₂O(l) → 3CNO^–(aq) + 2MnO₂(s) + H₂O + 2OH^–(aq)

3CN^–(aq) + 2MnO₄^–(aq) + H₂O(l) → 3CNO^–(aq) + 2MnO₂(s) + 2OH^–(aq)

d) H₂O₂(aq) + ClO₂(aq) → ClO₂^–(aq) + O₂(g)

1) Separate the half-reactions:

H₂O₂(aq) → O₂(g)

ClO₂(aq) → ClO₂^–(aq)

2) Balance the elements. Add H₂O to balance the O atoms, and H+ to balance the H atoms.

H₂O₂(aq) → O₂(g) + 2H⁺(aq)

ClO₂(aq) → ClO₂^–(aq)

3) Balance the charges by adding electrons.

H₂O₂(aq) → O₂(g) + 2H⁺(aq) + 2e^–

ClO₂(aq) + e^– → ClO₂^–(aq)

4) Balance the number of electrons by multiplying the equation(s) with a whole number.

H₂O₂(aq) → O₂(g) + 2H⁺(aq) + 2e^–

2ClO₂(aq) + 2e^– → 2ClO₂^–(aq)

5) Once everything is balanced, add the half-reactions together and check if all the atoms and charges are balanced again.

H₂O₂(aq) → O₂(g) + 2H⁺+ 2e^–

2ClO₂(aq) + 2e^– → 2ClO₂^–(aq)
_______________________________________

H₂O₂(aq) + 2ClO₂(aq) + 2e^– → O₂(g) + 2H⁺+ 2e^– + 2ClO₂^–(aq)

H₂O₂(aq) + 2ClO₂(aq) → O₂(g) + 2H⁺+ 2ClO₂^–(aq)

6) This is the balanced red-ox reaction in acidic media, so to obtain the one in a basic solution, we need to add 2OH^– on both sides of the equation:

H₂O₂(aq) + 2ClO₂(aq) + 2OH^–(aq) → O₂(g) + 2H⁺+ 2ClO₂^–(aq) + 2OH^–(aq)

The two H⁺ and OH^– ions are written as two water molecules:

H₂O₂(aq) + 2ClO₂(aq) + 2OH^–(aq) → O₂(g) + 2ClO₂^–(aq) + 2H₂O(l)

e) MnO₄^–(aq) + Fe(OH)₂(s) → MnO₂(s) + Fe(OH)₃(s)

1) Separate the half-reactions:

MnO₄^–(aq) → MnO₂(s)

Fe(OH)₂(s) → Fe(OH)₃(s)

2) Balance the elements. Add H₂O to balance the O atoms, and H+ to balance the H atoms.

MnO₄^–(aq) + 4H⁺(aq) → MnO₂(s) + 2H₂O(l)

Fe(OH)₂(s) + H₂O(l) → Fe(OH)₃(s) + H⁺(aq)

3) Balance the charges by adding electrons.

MnO₄^–(aq) + 4H⁺(aq) + 3e^–→ MnO₂(s) + 2H₂O(l)

Fe(OH)₂(s) + H₂O(l) → Fe(OH)₃(s) + H⁺(aq) + e^–

4) Balance the number of electrons by multiplying the equation(s) with a whole number.

MnO₄^–(aq) + 4H⁺(aq) + 3e^–→ MnO₂(s) + 2H₂O(l)

3Fe(OH)₂(s) + 3H₂O(l) → 3Fe(OH)₃(s) + 3H⁺(aq) + 3e^–

5) Once everything is balanced, add the half-reactions together and check if all the atoms and charges are balanced again.

MnO₄^–(aq) + 4H⁺(aq) + 3e^–→ MnO₂(s) + 2H₂O(l)

3Fe(OH)₂(s) + 3H₂O(l) → 3Fe(OH)₃(s) + 3H⁺(aq) + 3e^–

_______________________________________

MnO₄^–(aq) + 4H⁺(aq) + 3e^– + 3Fe(OH)₂(s) + 3H₂O(l) → MnO₂(s) + 2H₂O(l) + 3Fe(OH)₃(s) + 3H⁺ + 3e^–

MnO₄^–(aq) + H⁺(aq) + 3Fe(OH)₂(s) + H₂O(l) → MnO₂(s) + 3Fe(OH)₃(s)

6) This is the balanced red-ox reaction in acidic media, so to obtain the one in a basic solution, we need one OH^– on both sides of the equation:

MnO₄^–(aq) + H⁺(aq) + OH^–(aq) + 3Fe(OH)₂(s) + H₂O(l) → MnO₂(s) + 3Fe(OH)₃(s) + OH^–(aq)

The H⁺ and OH^– ions are written as a water molecule:

MnO₄^–(aq) + 3Fe(OH)₂(s) + 2H₂O(l) → MnO₂(s) + 3Fe(OH)₃(s) + OH^–(aq)

3 thoughts on “Balancing Redox Reactions”

Kenfack

November 6, 2022 at 1:57 am

I like your teaching method
MissJustine

March 31, 2023 at 2:12 pm

thank you for giving so many practice problems, they’ve been very helpful
- Dr. S. Gevorg
  
  March 31, 2023 at 11:38 pm
  
  Glad to hear that. Doing my best to make this as helpful as possible.

General Chemistry

Reactions in Aqueous Solutions

Balancing Redox Equations in Acidic Solution

Balancing Redox Equations in Basic Solution

To summarize the balancing of redox reactions, remember that:

Practice

3 thoughts on “Balancing Redox Reactions”

Leave a Comment Cancel reply