Earlier in the semester, or perhaps in your Chem II class, you learned about acid-base titrations which were used to determine the concentration of an acid or a base.

For this, we are using a standard solution (titrant) which is slowly added to the analyte until the indicator signals the equivalence point. The moles of the acid or the base in the analyte are determined based on the stoichiometry of the reaction with the component of the standard solutions.

The summary of acid-base titrations is shown in the image below and you can refer to the original article for more information.

 

 

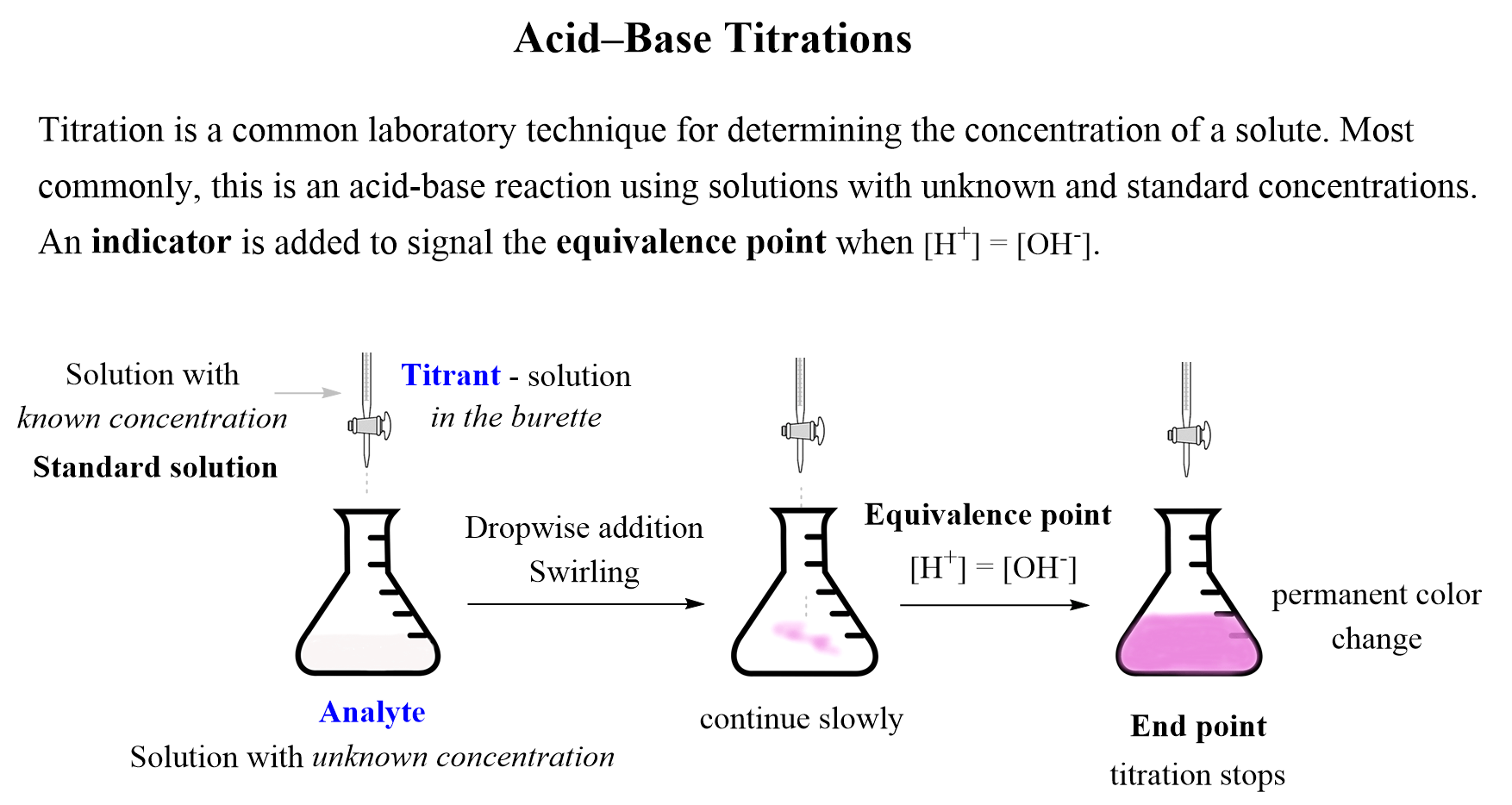
 Now, in this section of acid-base reactions, we will study the titrations in a little more detail, particularly focusing on how the pH changes during the experiment. The strategy to gain more insight to these experiments, is building a plot of the pH change vs the volume of the titrant added:  

 

 

The correlation between the pH and the volume of the solution depends on the nature of the acid and the base. Today, we will discuss the titration of a strong acid with a strong base or vice versa.

 

Strong Acid-Base Titrations

Let’s consider adding a 0.10 M NaOH solution to a 25.0 mL of a 0.10 M HCl solution:

 

NaOH(aq) + HCl (aq) → NaCl(aq) + H₂O(l)

 

Before the addition, there is only HCl in the solution, therefore, the solution is very acidic, so let’s calculate its pH. Remember, the HCl is a strong electrolyte completely dissociated into H⁺ (H₃O⁺) and Cl- ions, therefore, [H⁺] = [HCl]:

 

HCl (aq) → H⁺(aq) + Cl^–(aq)

 pH = -log [H⁺] = -log 0.10 = 1.0

 

To make a graph, we need the pH values at certain points of the NaOH addition.

 

 pH after Adding 5.00 mL NaOH

Before determining the pH after the addition of the base, let’s see how many moles of HCl we have initially in the solution:

 

\[{\rm{n}}\,{\rm{(HCl)}}\;{\rm{ = }}\,{\rm{0}}{\rm{.0250}}\,\cancel{{\rm{L}}}\,{\rm{ \times }}\,\frac{{{\rm{0}}{\rm{.10}}\,{\rm{mol}}}}{{{\rm{1}}\,\cancel{{\rm{L}}}}}\, = \,{\rm{0}}{\rm{.00250}}\,{\rm{mol}}\]

 

Next, we need to calculate the moles of NaOH in the 5.00 mL (0.00500 L) solution:

 

\[{\rm{n}}\,{\rm{(NaOH)}}\;{\rm{ = }}\,{\rm{0}}{\rm{.00500}}\,\cancel{{\rm{L}}}\,{\rm{ \times }}\,\frac{{{\rm{0}}{\rm{.10}}\,{\rm{mol}}}}{{{\rm{1}}\,\cancel{{\rm{L}}}}}\, = \,{\rm{0}}{\rm{.000500}}\,{\rm{mol}}\]

 

According to the balanced equation, this is how many moles of HCl will react too because of the 1:1 mole ratio:

 

NaOH(aq) + HCl (aq) → NaCl(aq) + H₂O(l)

 

To find the remaining amount of HCl in the solution, we subtract the reacted moles from its initial moles. Therefore, there will be 0.00250 – 0.000500 mol = 0.00200 mol HCl.

You can also make a little ICE table to visualize this. Instead of HCl and NaOH, we will label the columns as H⁺ and OH^–:

 

	mol OH–	mol H+
Before Addition	≈ 0	0.00250
Added	0.000500	–
Remaining	≈ 0	0.00200

 

To find the pH after the addition of 5.00 mL NaOH, we convert the 0.00200 moles to mol/L. Make sure to include the volume of the NaOH solution:

 

V (total) = 25.0 mL + 5.00 mL = 30.0 mL = 0.0300 L

 

 \[{\rm{M}}\,{\rm{(HCl)}}\;{\rm{ = }}\,\frac{{{\rm{0}}{\rm{.00200}}\,{\rm{mol}}}}{{{\rm{0}}{\rm{.0300}}\,{\rm{L}}}}\, = \,{\rm{0}}{\rm{.0667}}\,{\rm{mol/L}}\]

 

pH = -log [H⁺] = -log 0.0667 = 1.17

 

pH after Adding 10.0 mL NaOH

The pH is calculated as we did for the addition of 5.00 mL NaOH. The ICE table would be:

 

	mol OH–	mol H+
Before Addition	≈ 0	0.00250
Added	0.00100	–
Remaining	≈ 0	0.00150

 

\[{\rm{M}}\,{\rm{(HCl)}}\;{\rm{ = }}\,\frac{{{\rm{0}}{\rm{.00150}}\,{\rm{mol}}}}{{{\rm{0}}{\rm{.0250L  + }}\,{\rm{0}}{\rm{.010}}\,0\;{\rm{L}}}}\, = \,{\rm{0}}{\rm{.0429}}\,{\rm{mol/L}}\]

 

pH = -log [H⁺] = -log 0.0429 = 1.37

 

For the addition of 15 – 50 mL NaOH solution, the calculations are again done in an identical way. The following data represents the pH values at these intervals of the titration. 

 

 

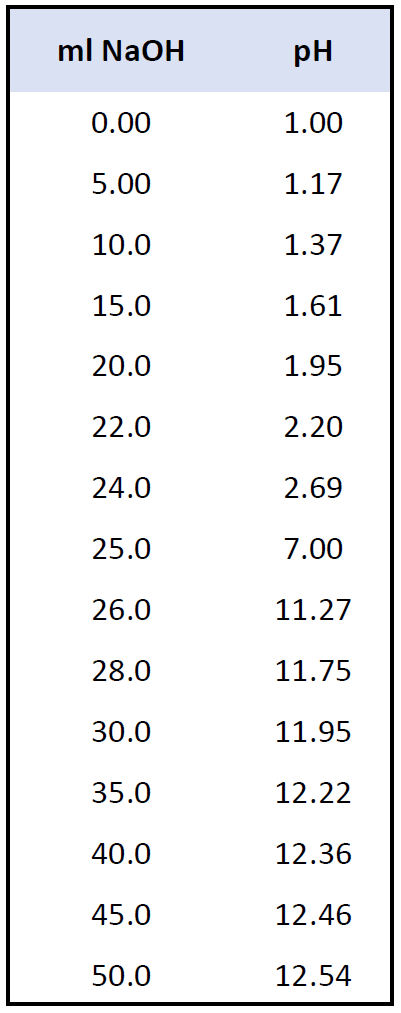
And now, let’s plot these values to make a graph:

 

 

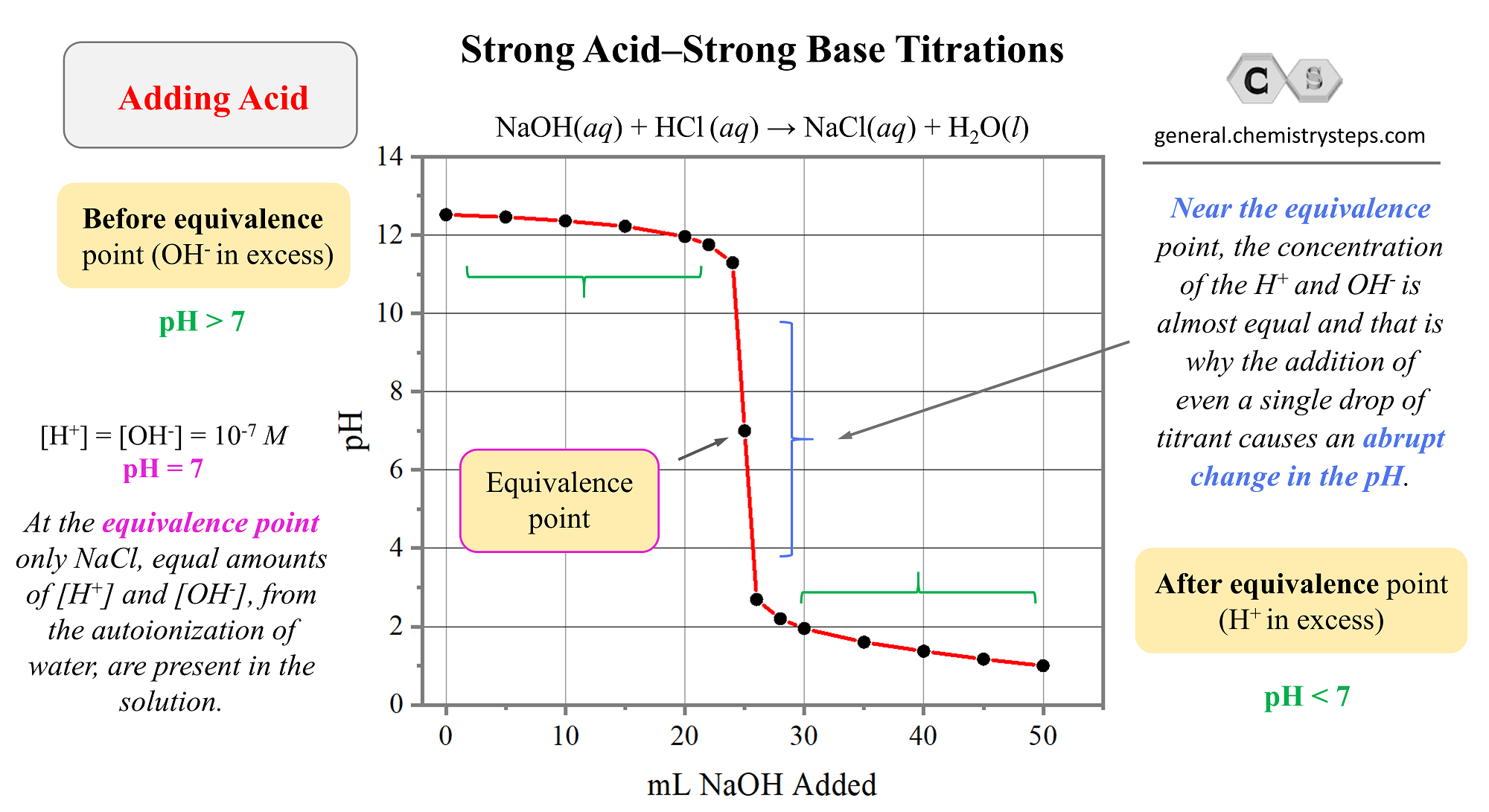
A few important observations on strong acid-base titrations from the graph :

1) The pH changes slowly in the first half of the titration.

2) The equivalence point is at pH 7 because it is reached when the number of moles of base added equals the number of moles of acid initially in the solution. At this point, there is no excess of H⁺ ions left in the solution as only contains NaCl which, as a salt of strong acid and a strong base, has no appreciable effect on pH.

3) Near the equivalence point, the concentration of the H⁺ and OH^– is almost equal and that is why the addition of even a single drop of titrant cause an abrupt change in the pH.

4) After the equivalence point, the predominant species in the solution are the OH^– ions because of the increasing excess of the added NaOH solution.

You may wonder; what is the base reacting with after the equivalence point if all the acid has been neutralized? Remember that in pure water there is always some H⁺ and OH^– ions and even when the OH^– ions start predominating, there is always traces of H⁺ ions.

 

Titration of Strong Base with Strong Acid

Conceptually, it is the same process except initially there is an excess of OH- ions which switches to the excess of H⁺ ions. Therefore, the graph is going to be like a mirror image of the one for titrating a strong acid with a strong base.

 

 

So, initially, the pH of the solution is very high because there is only NaOH in the solution. In the first half of the titration, the pH decreases gradually since the OH^– ions remain in excess. However, getting closer to the equivalence point, the pH starts decreasing quickly because the excess of OH- diminishes and the concentration of the OH^– and H⁺ ions are almost equal. At pH 7, the concentrations are finally equal both being 10^-7 M. The NaCl in the solution does not affect the pH because it is a slat of a strong acid HCl and strong base NaOH. After the equivalence point, the pH keeps decreasing as the portions now start predominating.

When solving problems related to strong acid-base titrations, react the acid and the base and determine the remaining concentration of H⁺ or OH^– ions. Pay attention to the volume of the solution – you should always add the volume of the titrant.

 

Check Also

• Buffer Solutions
• The Henderson–Hasselbalch Equation
• The pH of a Buffer Solution
• Preparing a Buffer with a Specific pH
• The Common Ion Effect
• The pH and pK_a Relationship
• Titration of a Weak Acid by a Strong Base
• Titration of a Weak Base by a Strong Acid
• Titration of Polyprotic Acids
• Buffer Solutions Practice Problems
• K_sp and Molar Solubility
• The Effect of a Common Ion on Solubility
• The Effect of pH on Solubility
• Will a Precipitate Form? K_sp and Q
• K_sp and Molar Solubility Practice Problems