pH of acetate buffer calculation

General Chemistry

There are two ways of calculating the pH of a buffer solution; the equilibrium approach and the one using the Henderson–Hasselbalch equation. The latter is shorter and is used more often. However, let’s start with the equilibrium approach so that we can see how the Henderson–Hasselbalch equation makes the process easier.

And before that, let’s also recall how we calculate the pH of a weak acid solution because calculating the pH of a buffer containing a weak acid and its conjugate base brings in just one additional step. 

 

The pH of a Weak Acid – Recap

Remember, we need to set up an ICE table to determine the concentration of hydronium ions at equilibrium based on the Ka value of the acid.

Let’s recall the process by determining, for example, the pH of 0.50 M solution of acetic acid (CH3CO2H). Ka = 1.7 x 10-5

First, write down the ionization equation and set the molarity of ionized acid as x mol/l.

 

 

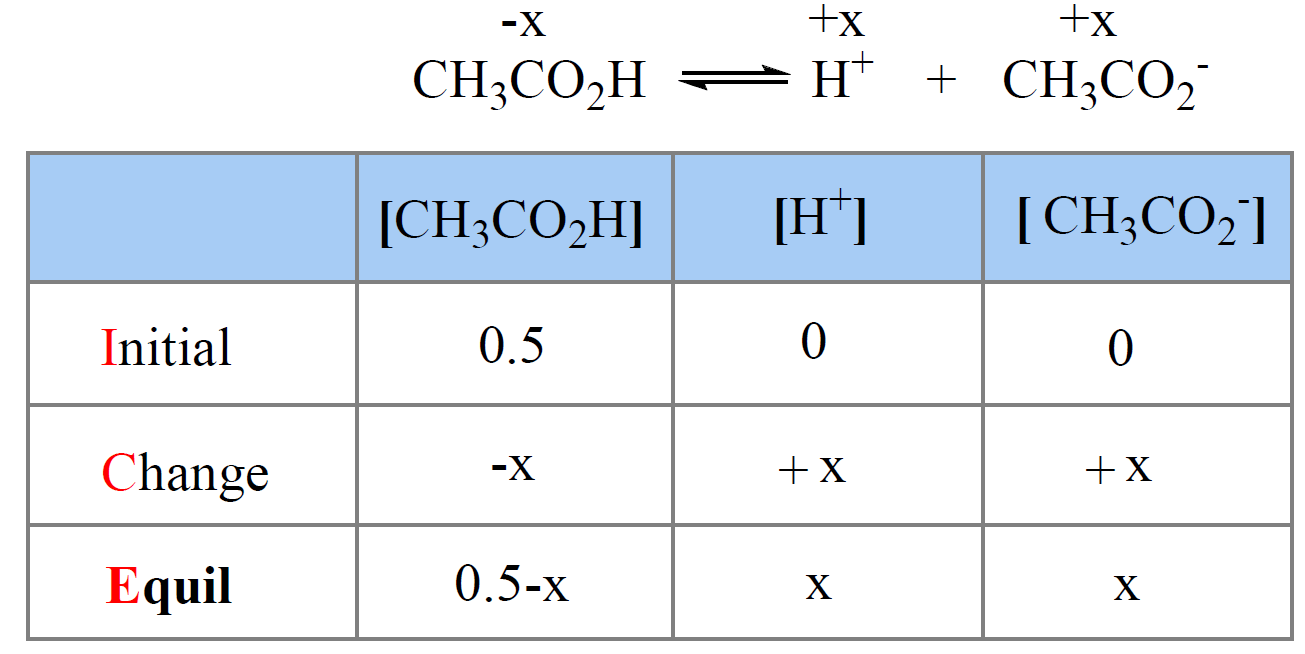
Next, we write the equilibrium constant expression and make an approximation that x << 0.50, therefore, 0.5 – x ≈ 0.5:

 

\[{K_{\rm{a}}}\; = \;\frac{{{\rm{[C}}{{\rm{H}}_{\rm{3}}}{\rm{C}}{{\rm{O}}_{\rm{2}}}^{\rm{ – }}{\rm{][}}{{\rm{H}}^{\rm{ + }}}{\rm{]}}}}{{{\rm{[C}}{{\rm{H}}_{\rm{3}}}{\rm{C}}{{\rm{O}}_{\rm{2}}}{\rm{H]}}}}\; = \;\frac{{\left( {\rm{x}} \right)\left( {\rm{x}} \right)}}{{0.5\, – \;x}}\; \approx \;\frac{{{{\rm{x}}^{\rm{2}}}}}{{0.5\,}}\; = \;1.7\; \times \;{10^{ – 5}}\]

 

x = 0.0029, so the pH = -log0.0029 = 2.5

  

And this is how we determine the pH of a weak acid.

 

The pH of a Buffer using the Equilibrium Approach

Now, let’s say we have a buffer that, in addition to the 0.50 M acetic acid, contains 0.20 M of its conjugate base sodium acetate (CH3CO2Na).

Calculate the pH of this buffer solution?

The difference here, compared to the solution with only acetic acid, is that the equilibrium concentration of CH3CO2– is going to be higher by 0.20 M because CH3CO2Na is a strong electrolyte and therefore completely dissociates into ions.

So, we need to write two equations: one for the concentration of H3O+ ions and the other for the concentration of the acetate ions because these two go into the expression of Ka.

 

 

The total concentration of the acetate ion at equilibrium is the sum of 0.20 M from the salt and x M from the dissociation of acetic acid.

The equilibrium constant is then equal to:

 

\[{K_{\rm{a}}}\; = \;\frac{{{\rm{[C}}{{\rm{H}}_{\rm{3}}}{\rm{C}}{{\rm{O}}_{\rm{2}}}^{\rm{ – }}{\rm{][}}{{\rm{H}}^{\rm{ + }}}{\rm{]}}}}{{{\rm{[C}}{{\rm{H}}_{\rm{3}}}{\rm{C}}{{\rm{O}}_{\rm{2}}}{\rm{H]}}}}\;\; = \;\frac{{\left( {\rm{x}} \right)\left( {{\rm{0}}{\rm{.2  +  x}}} \right)}}{{0.5\, – \;x}}\; = \;1.7\; \times \;{10^{ – 5}}\]

 

Making the approximation that x << 0.2 and x << 0.5, we get that:

 

\[{K_{\rm{a}}}\; = \;\frac{{{\rm{[C}}{{\rm{H}}_{\rm{3}}}{\rm{C}}{{\rm{O}}_{\rm{2}}}^{\rm{ – }}{\rm{][}}{{\rm{H}}^{\rm{ + }}}{\rm{]}}}}{{{\rm{[C}}{{\rm{H}}_{\rm{3}}}{\rm{C}}{{\rm{O}}_{\rm{2}}}{\rm{H]}}}}\;\; = \;\frac{{\left( {\rm{x}} \right)\left( {{\rm{0}}{\rm{.2  +  }}\cancel{{\rm{x}}}} \right)}}{{0.5\, – \;\cancel{x}}}\; \approx \;\frac{{{\rm{0}}{\rm{.2x}}}}{{0.5\,}}\; = \;1.7\; \times \;{10^{ – 5}}\]

 

x = 4.3 x 10-5

Check the approximation dividing by the initilal concenrtation of acetic acid: 4.3 x 10-5/0.5 = 0.0086 % – valid

Therefore, the pH is:

 

pH = -log4.3 x 10-5 = 4.37

 

To summarize, calculating the pH of a buffer based on the equilibrium approach, is very similar to what we do in pH calculations of weak acids and bases. The only difference is that the initial concentration of the conjugate base (or acid if it is a buffer of a weak base and its salt) is not zero in the ICE table.

Let’s now see how the pH of a buffer can be calculated using the Henderson–Hasselbalch Equation.

 

The pH of a Buffer using the Henderson–Hasselbalch Equation

Let’s work on the same example to compare the two methods.

Calculate the pH of a solution containing 0.50 M CH3CO2H and 0.20 M CH3CO2Na. pKa (CH3CO2H) = 4.75

The Henderson–Hasselbalch equation can be shown as:

 

 

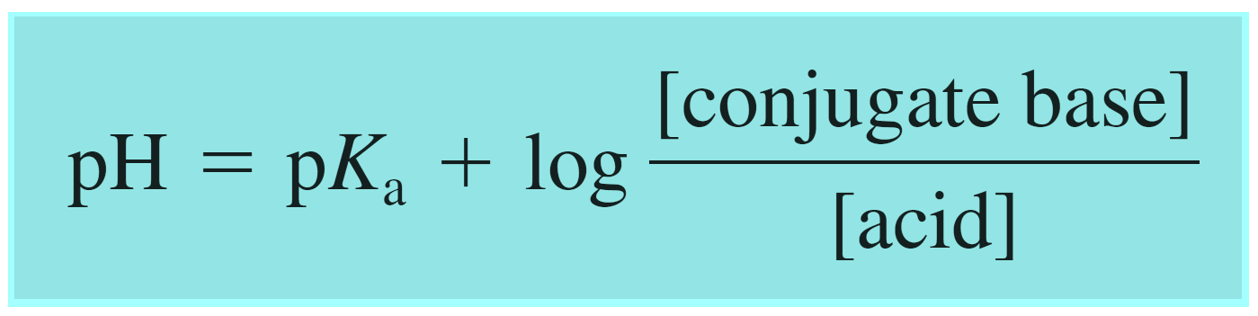
Where [conjugate base] or [A–] would be the concentration of the acetate ion (CH3CO2Na), and [acid] or [HA] is the concentration of the acetic acid. So, we can write that:

 

 

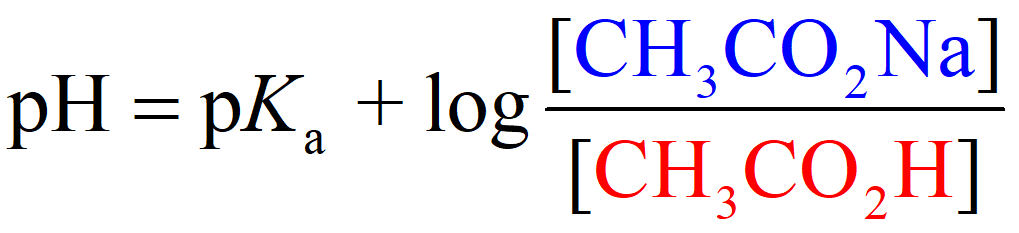
Now, these are the equilibrium concentrations, and we know that it is 0.20 M for the acetate ion because it is completely dissociated. However, acetic acid is a weak acid and not all of it dissociates into ions. In fact, very little of it does, and the question is if we are still going to use an ICE table to determine the concentration of H3O+ ions, then what is the advantage of using the Henderson–Hasselbalch equation?

Fortunately, the answer is no – we don’t usually need to set up an ICE table to calculate the pH of a buffer solution.

The key here lies in the fact that acetic acid is a weak acid, and just like we did before, we make an approximation that the amount of the acid that dissociates is very little compared to the initial concentration of the acid, and therefore, the equilibrium concentration of the acid is the same as its initial concentration. So, it was 0.5 M initially then very little of it dissociated (x M), but because it is very little, we just assume the equilibrium concentration is about the same as the initial.

And at this point, we only need to plug in the numbers for the initial concentration given in the table:

 

 

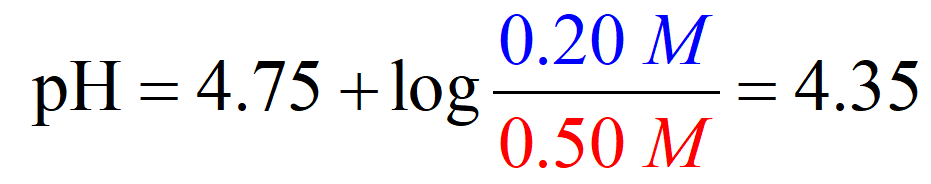
Comparing the two methods, we have a pH of 4.35 vs 4.37 and this shows that we can make an approximation that x is very small and use the initial concentrations of the buffer components to determine the pH.

Remember that, in general, we can only make the approximation for x being very small if: (a) the initial concentrations of acids (and/or bases) are large enough, and (b) the equilibrium constant is fairly small. As a guideline, when determining the concentration of a buffer solution, use the Henderson–Hasselbalch equation if the [HA] or [Base] > 0.10 and it is at least 103 times greater than the equilibrium constant.

 

Buffers Containing a Base and Its Conjugate Acid

In the example above, we had a buffer composed of an acid and its conjugate base. However, remember, that a buffer can also be composed of a base and its conjugate acid which, unlike a regular acid, is an ion. Although this does not change the principle, you can write the Henderson–Hasselbalch equation using the words “base and acid”, instead of conjugate base and acid to avoid any confusion:

 

 

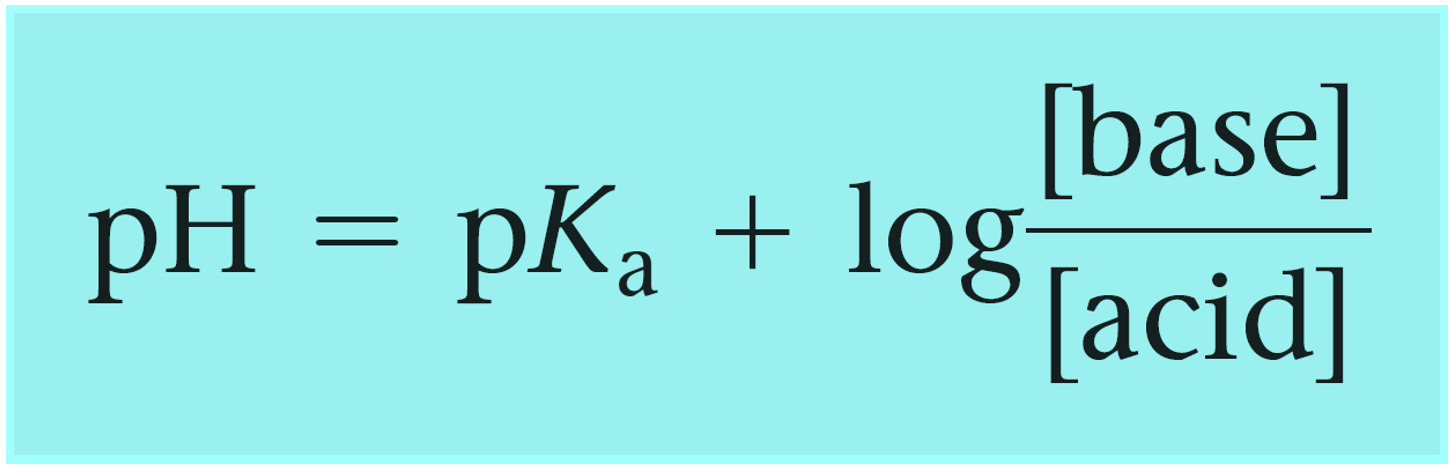
One common example of such buffer is the solution of weak base ammonia (NH3) and its conjugate acid ammonium chloride (NH4Cl).

The strategy for calculating the pH is similar to what we did before for the buffers containing a weak acid and its conjugate base.

The only extra step that you may need to do is to determine the pKa of the conjugate acid using its relationship to the pKb:

 

pKa + pKb = 14

For example,

Calculate the pH of a buffer solution containing 0.60 M in NH3 and 0.35 M in NH4Cl. The pKb of ammonia is 4.75.

The first step is to determine the pKa so that we can use it in the Henderson–Hasselbalch equation:

 

pKa + pKb = 14

pKa = 14 – pKb = 14 – 4.75 = 9.25

 

Because the concentrations of the buffer components are significantly higher than the Kb of ammonia, all we need to do, at this point, is plugging the numbers in the equation:

 

\[{\rm{pH}}\; = \;{\rm{p}}{K_{\rm{a}}}\;{\rm{ + }}\;{\rm{log}}\frac{{{\rm{[}}{{\rm{A}}^{\rm{ – }}}{\rm{]}}}}{{{\rm{[HA]}}}}\]

 

\[{\rm{pH}}\; = \;9.25\;{\rm{ + }}\;{\rm{log}}\frac{{{\rm{[0}}{\rm{.60]}}}}{{{\rm{[0}}{\rm{.35]}}}}\; = \;9.5\]

 

The Henderson–Hasselbalch equation gives some quick information and hints on choosing a proper buffer correlating pKa and the pH of the solution, and this is what we will discuss in the next couple of articles.

 

Check Also

 

Leave a Comment