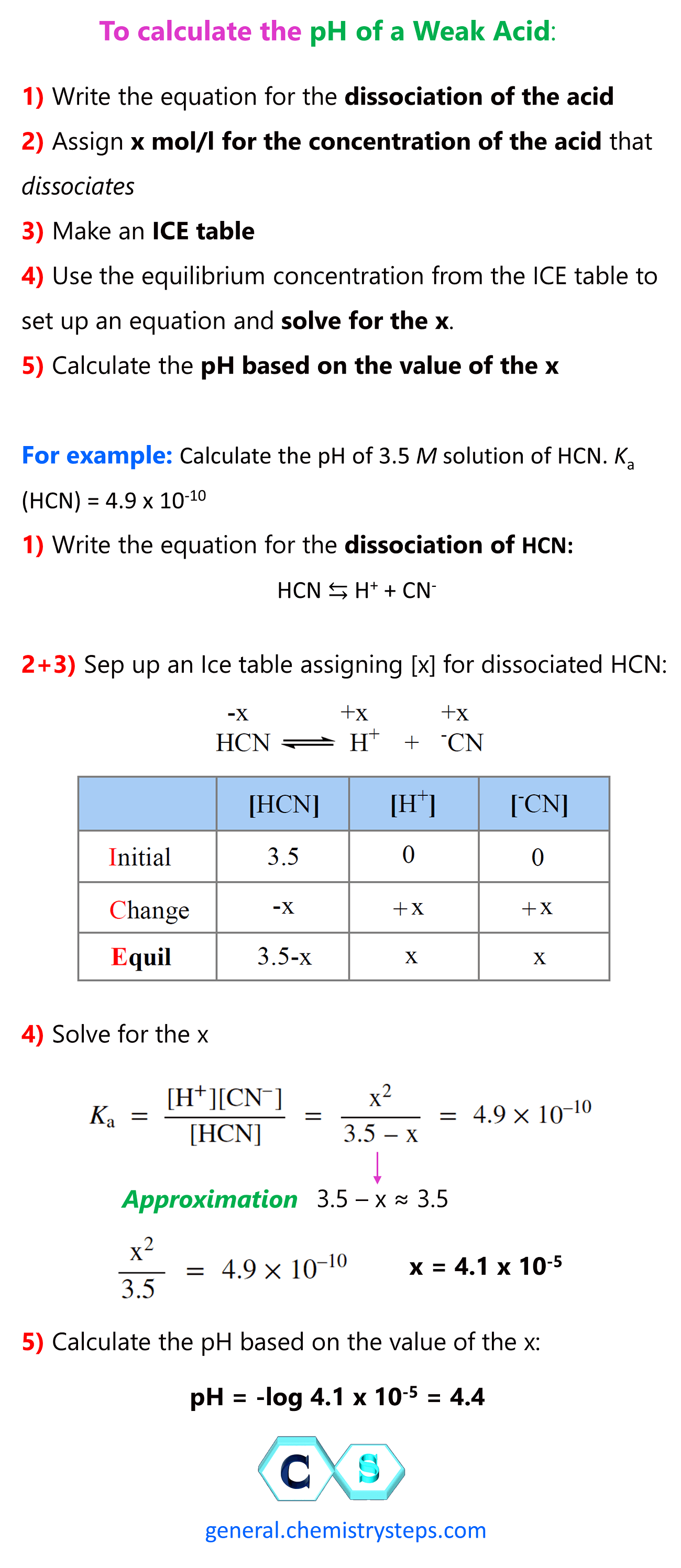
Determining the pH of a weak acid is more complex compared to what we saw for strong acids, because for a weak acid, the dissociation is not 100%, and therefore, the [H+] is not the same as [HA].
For example: Calculate the pH of 3.5 M solution of HCN. Ka (HCN) = 4.9 x 10-10
Now regardless of the nature of the acid, the pH is calculated with the same formula:
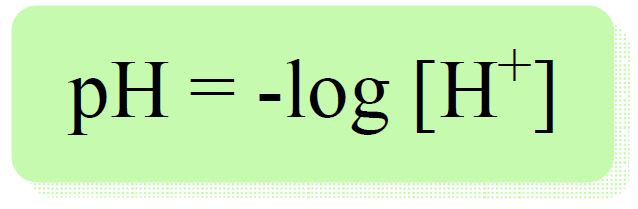
Therefore, we need to determine the concentration of portions. To do this, we need to go back a little bit and recall the ICE tables used in determining the equilibrium concentrations.
First, let’s write the dissociate equation of HCN:
HCN ⇆ H+ + CN–
Now, initially, the concentration of HCN is 3.5 M, but we don’t know how much of it is going to dissociate into H+ ions. Therefore, we assign x M as the concentration of HCN that dissociate (change in the ICE table), and make an ICE table for the initial, reacted, and equilibrium concentrations of all species in the dissociation equation.
The initial concentration of H+ and CN– ions are 0, but at equilibrium, they are going be x mol/l because that is how much the HCN dissociates. The equilibrium concentration of HCN is going to be decreased by x mol/l, so it is (3.5 -x) M.
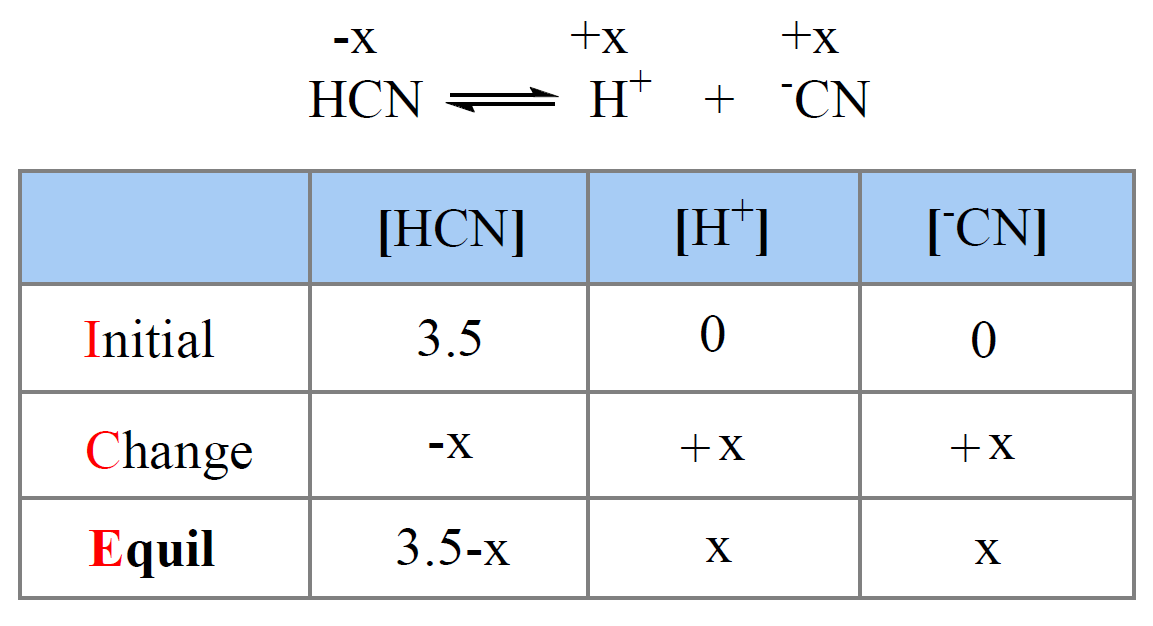
Next, we set up the equation based on the Ka:
\[{K_{\rm{a}}}\, = \,\frac{{{\rm{[}}{{\rm{H}}^{\rm{ + }}}{\rm{][C}}{{\rm{N}}^{\rm{ – }}}{\rm{]}}}}{{{\rm{[HCN]}}}}\; = \;\frac{{{{\rm{x}}^{\rm{2}}}}}{{{\rm{3}}{\rm{.5}}\;{\rm{ – }}\;{\rm{x}}}}\; = \;{\rm{4}}{\rm{.9 }} \times {\rm{ 1}}{{\rm{0}}^{{\rm{ – 10}}}}\]
This is a quadratic equation and remember a shorter way of solving it to use an approximation that 3.5- -x ≈ 3.5 because the dissociation constant is very small and therefore, the percentage of acid dissociation is negligible compared to its initial concentration (x << 3.5).
By doing so, we get a simplified equation:
\[\;\frac{{{{\rm{x}}^{\rm{2}}}}}{{{\rm{3}}{\rm{.5}}\;}}\; = \;{\rm{4}}{\rm{.9 }} \times {\rm{ 1}}{{\rm{0}}^{{\rm{ – 10}}}}\]
Therefore, x = 4.1 x 10-5
Make sure the approximation is valid, and for this, x must be less than 5% of HCN initial concentration (less than 5% of the acid dissociates). 4.1 x 10-5/3.5 = 0.0012%, so the approximation is valid. If it is not, you need to determine the x by solving the quadratic equation.
So, x = 4.1 x 10-5 , and this is the [H+] at equilibrium, therefore,
pH = -log 4.1 x 10-5 = 4.4
The ratio of [H+] at equilibrium over the initial concentration of acid is called percent ionization of a weak acid.
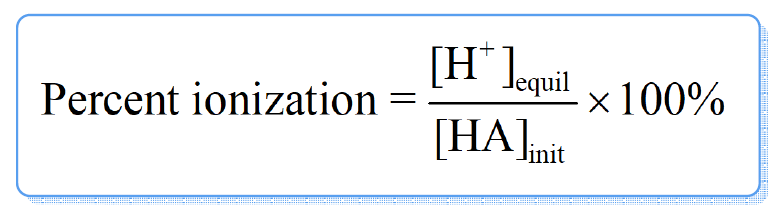
If the percent ionization < 5%, the approximation was valid.
To summarize calculating the pH of a weak acid, follow these steps:
1) Write the equation for the dissociation of the acid
2) Assign x mol/l for the concentration of the acid that dissociates
3) Make an ICE table
4) Use the equilibrium concentration from the ICE table to set up an equation and solve for the x.
5) Calculate the pH based on the value of the x
Check Also
- Definitions of Acids and Bases
- Acid-Base Reactions
- Acid-Base Titrations
- Conjugate Acid and Conjugate Base
- Autoionization of Water and Kw
- The pH and Acidity
- Acid Strength, Ka, and pKa
- Base Strength, Kb and pKb
- Ka, pKa, Kb, and pKb Relationship
- The pH of a Strong Acid and Base
- pH + pOH = 14
- The pH of a Weak Base
- ThepH of Polyprotic Acids
- The acidity of a Salt Solution
- The pH of a Salt Solution
- The pH of Salts With Acidic Cations and Basic Anions
- Acids and Bases Practice Problems
