In the previous post, we talked about determining the pH of a weak acid. Remember, the main challenge here is that weak acids do not dissociate by 100%, and therefore, the [H+] is not the same as [HA].
To determine the [H+], we set up an ICE table and determine the equilibrium concentrations of all the species in the chemical equation of the dissociation.
Now, for the pH of a weak base, it is the same strategy with a couple of extra steps. Let’s see how it works with an example of a weak base ammonia (NH3).
Example: Calculate the pH of a 1.5 M solution of ammonia. Kb = 1.8 x 10-5
The first step is to write the reaction of the weak base water! Remember, the water in this case acts as an acid and donates a proton to the base:
NH3(aq) + H2O(l) ⇆ NH4+(aq) + OH–(aq)
Next, assume x mol/l NH3 has reacted and set up an ICE table. Initially, the concentration of NH3 is 1.5 M, and its equilibrium concentration is going to be decreased by x mol/l, so it is (1.5 – x) M.
The initial concentration of NH4+ and OH– ions is 0, and at equilibrium they are going be x mol/l because that is how much of the ammonia reacts with water.
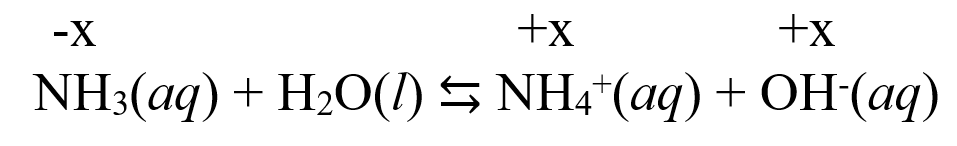
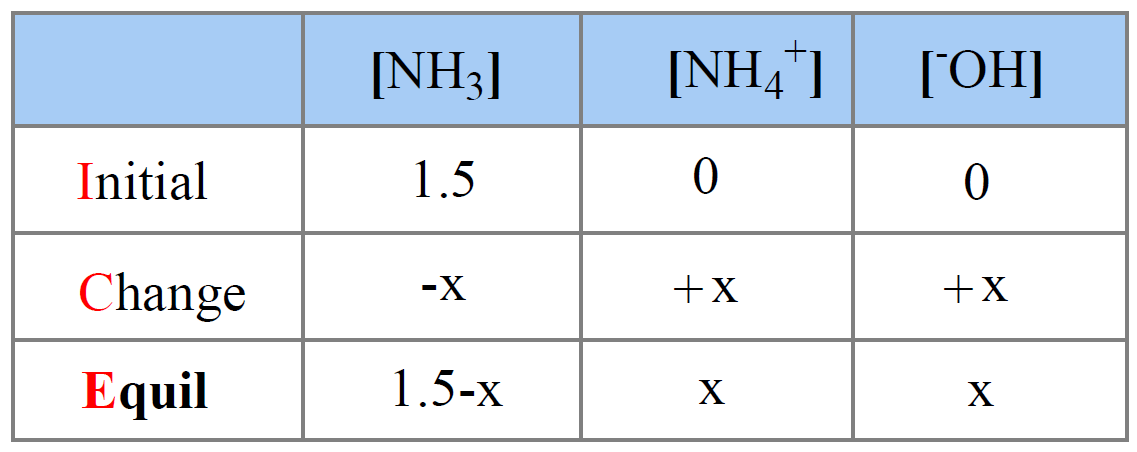
The expression for the equilibrium constant will then be:
\[{K_{{\rm{b}}}}\; = \,\frac{{{\rm{[N}}{{\rm{H}}_{\rm{4}}}^{\rm{ + }}{\rm{][O}}{{\rm{H}}^{\rm{ – }}}{\rm{]}}}}{{{\rm{[N}}{{\rm{H}}_{\rm{3}}}{\rm{]}}}}\; = \;\frac{{{{\rm{x}}^{\rm{2}}}}}{{{\rm{1}}{\rm{.5}}\;{\rm{ – }}\;{\rm{x}}}}\; = \;{\rm{1}}{\rm{.8 }} \times {\rm{ 1}}{{\rm{0}}^{{\rm{ – 5}}}}\]
This is a quadratic equation and remember a shorted way of solving it to use an approximation that 1.5- -x ≈ 1.5 because the ionization constant of the weak is very small and therefore, the percentage of it reacted with water is negligible compared to its initial concentration.
Doing so, we get a simplified equation:
\[\;\frac{{{{\rm{x}}^{\rm{2}}}}}{{{\rm{1}}{\rm{.5}}\;}}\; = \;{\rm{1}}{\rm{.8 }} \times {\rm{ 1}}{{\rm{0}}^{{\rm{ – 5}}}}\]
Therefore, x = 0.0052
Make sure the approximation is valid, and for this, x must be less than 5% of NH3 initial concentration:
\[\frac{{{\rm{0}}{\rm{.0052}}}}{{{\rm{1}}{\rm{.5}}\;}}\; \times \;100\% = \;{\rm{0}}{\rm{.34\% }}\]
Therefore, the approximation was valid and the concentration of OH– ion is 0.0052 M and we can calculate the pOH:
pOH = -log [-OH] = -log 0.0052 = 2.3
And finally, we can calculate the pH using the pH and pOH correlation:
pH =14 – pOH = 14 – 2.3 = 11.7
Alternatively, we can determine the concentration of H+ ions from the relationship [OH–] · [H+] = Kw = 10-14.
\[\left[ {{{\rm{H}}^{\rm{ + }}}} \right]\;{\rm{ = }}\,\frac{{{K_{\rm{w}}}}}{{\left[ {{\rm{O}}{{\rm{H}}^{\rm{ – }}}} \right]}}\; = \,\frac{{1.0\, \times {{10}^{ – 14}}}}{{0.0052}}\, = \,1.923\, \times \,{10^{ – 12}}\]
pH = -log [H+] = -log 1.923 x 10-12 = 11.7
pH 11.7 indicates a basic solution which additionally suggests that our calculations were correct because ammonia is a base.
To summarize calculating the pH of a weak base, follow these steps:
1) Write the equation for the reaction of the base with water
2) Assign x mol/l for the concentration of the base that reacts with water
3) Make an ICE table
4) Use the equilibrium concentration from the ICE table to set up an equation and solve for the x.
5) Calculate the pOH based on the value of the x
6) Calculate the pH using the pH + pOH = 14 relationship
Check Also
- Definitions of Acids and Bases
- Acid-Base Reactions
- Acid-Base Titrations
- Conjugate Acid and Conjugate Base
- Autoionization of Water and Kw
- The pH and Acidity
- Acid Strength, Ka, and pKa
- Base Strength, Kb and pKb
- Ka, pKa, Kb, and pKb Relationship
- The pH of a Strong Acid and Base
- pH + pOH = 14
- The pH of a Weak Base
- ThepH of Polyprotic Acids
- The acidity of a Salt Solution
- The pH of a Salt Solution
- The pH of Salts With Acidic Cations and Basic Anions
- Acids and Bases Practice Problems
