General Chemistry

Definition of acids and bases, identifying them along with the conjugate acid and conjugate base, pH of strong and weak acids and bases, the pH and pOH relationship, Ka and Kb, pKa and Ka correlation, the acid-base properties of salts, identifying the acidity of the salt based on the acid and the base it is prepared from, and calculating the pH of salt solutions. This is what is covered in this summary practice problem set on acids and bases.

 

The links to corresponding topics are given below:

 

Practice

1.

Identifying Acids and Bases

 

Write the chemical equation for the ionization reaction and the corresponding Ka equilibrium expression for each acid.

(a) HCN, (b)  H2S, (c)  C5H5NH+, (d) HF

a)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
b)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
c)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
d)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
2.

In each reaction, identify the acid, base, conjugate acid, and the conjugate base according to the Brønsted–Lowry acid-base theory.

 

(a) H2SO3(aq) + H2O(l) → H3O+(aq) + HSO3–(aq)

(b) CH3NH3+(aq) + OH–(aq) → CH3NH2(aq) + H2O(l)

(c) H2PO4–(aq) + NH3(aq) → HPO42-(aq) + NH4+(aq)

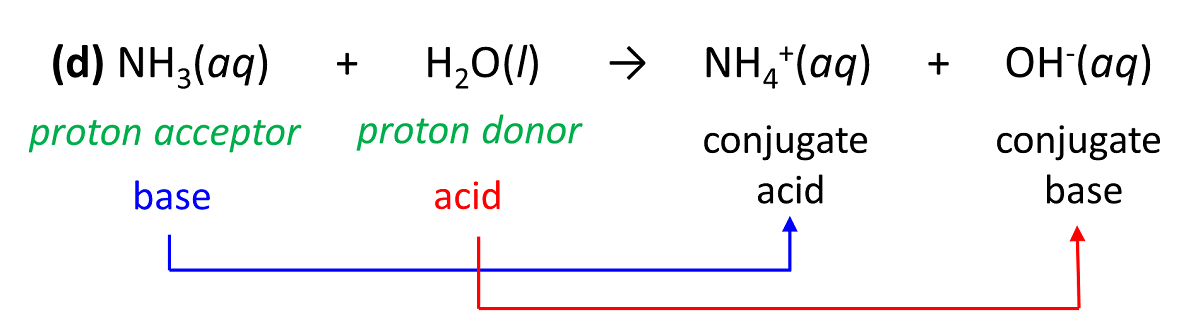
(d) NH3(aq) + H2O(l) → NH4+(aq) + OH–(aq)

(e) CH3CH2NH2(aq) + H2O(l) → CH3CH2NH3+(aq) + OH–(aq)

(f) HClO3(aq) + H2O(l) → H3O+(aq) + ClO3–(aq)

(g) CH3COO2–(aq) + HCN(aq) → CH3COOH(aq) + CN–(aq)

(h) C5H5N(aq) + H2O(l) → C5H5NH+(aq) + OH–(aq)

(i) CO32-(aq) + H2O(l) → HCO3–(aq) + OH–(aq)

(j) HBr(aq) + H2O(l) → H3O+(aq) + Br–(aq)

(k) HClO(aq) + CH3NH2(aq) → CH3NH3+(aq) + ClO–(aq)

(l) HCO3–(aq) + C5H5NH+(aq) → H2CO3(aq) + C5H5N(aq)

 

a)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
b)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
c)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
d)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
e)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
f)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
g)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
h)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
i)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
j)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
k)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
l)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
3.

Acid Strength

 

Which of the following is the strongest acid: HCl (Ka = 1.3 x 106), CH3CH2NH3+( Ka = 2.5 x 10-11), and H2SO3 (Ka = 5.9 x 10-2)?

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
4.

Which of the following is the weakest acid: HClO3, HCN, or HC2H3O2?

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
5.

Given the pKa of each acid, determine the stronger conjugate base:

a) H2SO3 (pKa 8.1) vs CH3COOH (pKa 4.75)

b) HClO3 (pKa < 1) vs H3PO4 (pKa12)

c) HCN (pKa 2.1) vs H2SO4(pKa < 1)

d) HNO2 (pKa 3.2) vs HI (pKa < 1)

a)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
b)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
c)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
d)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
6.

Autoionization of Water and pH

 

Arrange the following solutions in the order of increasing acidity (least acidic to most acidic):

(a) pH = 9.8

(b) pH = 1.2

(c) pH = 4.7

(d) pH = 6.4

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
7.

Arrange the following solutions in the order of increasing basicity (least basic to most basic):

(a) pOH = 5.2

(b) pOH = 11.6

(c) pOH = 3.4

(d) pOH = 1.9

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
8.

Calculate the pH for each of the following solutions at 25 oC:

(a) [H3O+] = 1.3 x 10-2 M

(b) [H3O+] = 1.6 x 10-3 M

(c) [OH–] = 1.8 x 10-3 M

a)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
b)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
c)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
9.

 Calculate the [OH–] of each of the following solutions at 25 oC. Identify the solution as neutral, acidic, or basic.

a) [H+] = 2.5 x 10-6 M

b) [H+] = 8.3 x 10-4 M

c) [H+] = 4.6 M

d) [H+] = 3.9 x 10-2 M

a)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
b)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
c)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
d)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
10.

Given the pH values, calculate [H3O+] and [OH–] for each solution at 25 oC. Identify each solution as neutral, acidic, or basic.

a) pH = 7.20

b) pH = 15.3

c) pH = 4.60

a)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
b)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
c)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
11.

The pH of Strong Acids and Bases

 

Calculate the pH for each of the following solutions:

(a) 0.15 M HCl

(b) 0.60 M HClO4

(c) 1.4 M KOH

a)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
b)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
c)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
12.

Calculate the pH of each of the following solutions:

(a) 0.0025 M HI, (b) 0.84 M NaOH

a)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
b)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
13.

Calculate the pH of the solution prepared by dissolving 24.0 g of HCl in 662 mL of water.

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
14.

How many grams of KOH is needed to prepare a 680.0 mL solution with a pH of 9.80?

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
15.

Calculate the pH of the solution prepared by diluting 40.0 mL of 3.00 M HNO3 with 210.0 mL of water.

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
16.

The pH of Weak Acids

 

Calculate the pH of a 0.45 M solution of HCN. Ka (HCN) = 4.9 x 10-10

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
17.

Calculate the pH of a 0.74 M solution of acetic acid. Ka (CH3CO2H) = 1.7 x 10-5

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
18.

0.86 g benzoic acid (C6H5CO2H, Ka = 6.4 x 10-5) was dissolved in enough water to make 1.0 L of solution. Calculate the pH and concentration of all species present in the solution.

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
19.

Calculate the pH of a 2.0 M solution of hydrofluoric acid, HF if Ka (HF) = 6.6 x 10-4

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
20.

What is the acid ionization constant (Ka) of a weak acid (HA) if its 0.246 M solution has a pH of 2.68?

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
21.

A solution of nitrous acid (HNO2, Ka = 7.2 x 10-4) has a pH of 3.1. What was the initial concentration of nitrous acid in the solution?

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
22.

Calculate the pH of a 0.40 M H2S solution given that Ka1 = 1.0 x 10-7; Ka2 = 1.0 x 10-19.

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
23.

The pH of Weak Bases

 

Explain why all of these are weak bases by writing the equations for their reaction with water and the corresponding expression for Kb.

(a) NH3 (b)  HCO3– (c)  CN- (d) CH3NH2 (e) C5H5N (f) F–

a)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
b)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
c)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
d)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
e)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
f)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
24.

Determine the pH of a 0.85 M solution of ammonia (NH3).

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
25.

Triethylamine, (C2H5)3N is a common organic weak base with Kb of 4.0 x 10-4 . Calculate [OH–], [H+], and the pH of 0.25 M solution of triethylamine.

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
26.

Calculate [OH–], [H+], and the pH of 0.40 M solution of caffeine (pKb = 10.4).

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
27.

Calculate the percentage of ethyl amine (CH3CH2NH2) that is ionized by reacting with water in its 0.64 molar aqueous solution (Kb = 5.6 x 10-4).

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
28.

Morphine is among the most popular alkaloids that are used as pain killers. Like all the others, it contains a nitrogen atom which makes it a weak base. What is the Kb of morphine at a certain temperature if its 0.340 M solution has a pH of 10.9?

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
29.

The Acid–Base Properties of Salts

 

For each ion, determine if it acts as a weak base in an aqueous solution. For those that do, write an equation to show why they make the solution basic.

 

a) Cl– b) BrO– c) CN– d) ClO3– e) CH3CO2– f) I– g) NO2– h) F–

a)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
b)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
c)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
d)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
e)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
f)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
g)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
h)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
30.

Predict whether the aqueous solutions of the following compounds are acidic, basic, or neutral: (a) KBr (b) FeCl2, (c) Na2CO3, (d) Al(NO3)3 (e) KClO4, (f) Na2SO3, (g) NH4ClO3

a)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
b)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
c)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
d)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
e)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
f)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
g)
answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
31.

Which of the following salts would produce the most basic aqueous solution?

KF b. NaBr c. NH4Cl d. MgCl2 e. Mg(NO3)2

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
32.

Calculate the pH of a 0.74 M solution of NaOBr (Ka HBrO = 2.90 x 10-9).

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
33.

Calculate the pH of the 0.26 M solution of NH4ClO3 (Kb NH3 = 1.8 x 10-5).

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
34.

Calculate the pH of a 0.35 M solution of KNO2 (Ka = 4.0 x 10-4).

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
35.

Calculate the pH of a 1.0 M solution of sodium acetate (CH3CO2Na) considering that the Ka of acetic acid (CH3CO2H is 1.7 x 10-5.

answer
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  
Solution
This content is available to registered users only. Click here to Register! By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.  

Leave a Comment