In the previous post, we talked about the concept of chemical equilibrium which is reached when the rates of forward and reverse reactions are equal and thus the concentrations of the reactants and products stay constant.
Now, we say that the concentrations stay constant, but are they correlated in any way? It turns out that regardless of their values there is always a characteristic number describing the correlation between the concentrations of all the components in a chemical equilibrium. This constant is called the equilibrium constant, K or Kc.
For a general reaction, the equilibrium constant is given by the following equation:
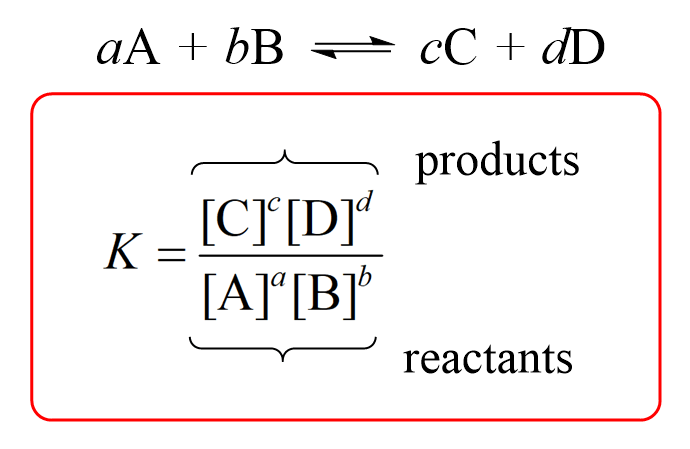
where a, b, c, and d – respective stoichiometric coefficients in the chemical equation, and the square brackets represent the molar concentrations.
Example:
At a particular temperature, it is determined for the reaction
2NO(g) + 2H2(g) ⇆ N2 (g) + 2H2O(g)
that at equilibrium, the concentrations are as follows: [NO(g)] = 3.2 x 10-3 M, [H2(g)] = 6.7 x 10-6 M, [N2(g)] = 4.8 x 10-2 M, and [H2O(g)] = 2.4 x 10-2 M. What is the value of the equilibrium constant K for the reaction at this temperature?
Solution
The equilibrium constant is the ratio of the equilibrium concentrations of the products and reactants, each raised to a power equal to its stoichiometric coefficient in the balanced equation.
\[K = \frac{{[{{\rm{N}}_{\rm{2}}}]{{[{{\rm{H}}_{\rm{2}}}{\rm{O}}]}^{\rm{2}}}}}{{{{[{\rm{NO}}]}^{\rm{2}}}{{[{{\rm{H}}_{\rm{2}}}]}^2}}}\]
\[K = \frac{{(4.8 \times {{10}^{ – 2}}){{(2.4 \times {{10}^{ – 2}})}^{\rm{2}}}}}{{{{(3.2 \times {{10}^{ – 3}})}^{\rm{2}}}{{(6.7 \times {{10}^{ – 6}})}^2}}} = 6.0 \times {10^{10}}\]
Equilibrium constants are temperature-dependent; therefore, the temperature must be given when citing a value of Kc.
For the given temperature, however, the equilibrium constant always has the same value, no matter what the individual equilibrium concentrations are.
For example, the equilibrium constant for the synthesis of ammonia at 298 K is Kc = 4.2 x 108, and at 400 K, Kc = 4.5 x 104.
3 H2(g) + N2(g) ⇆ 2 NH3(g)
\[K = \frac{{{{{\rm{[N}}{{\rm{H}}_{\rm{3}}}{\rm{]}}}^{\rm{2}}}}}{{{\rm{[}}{{\rm{N}}_{\rm{2}}}{\rm{][}}{{\rm{H}}_{\rm{2}}}{{\rm{]}}^{\rm{3}}}}}\]
Kc (298 K) = 4.2 x 108
Kc (400 K) = 4.5 x 104
Notice that the equilibrium constant is unitless even though if we plug units of molarity raised to different powers, we’d expect to have units.
The reason for this is that the accurate expression for the equilibrium constant uses the activities of the components and their molarities.
So, for the equilibrium constant of a general reaction, we’d write:
aA + bB ⇆ cC + dD
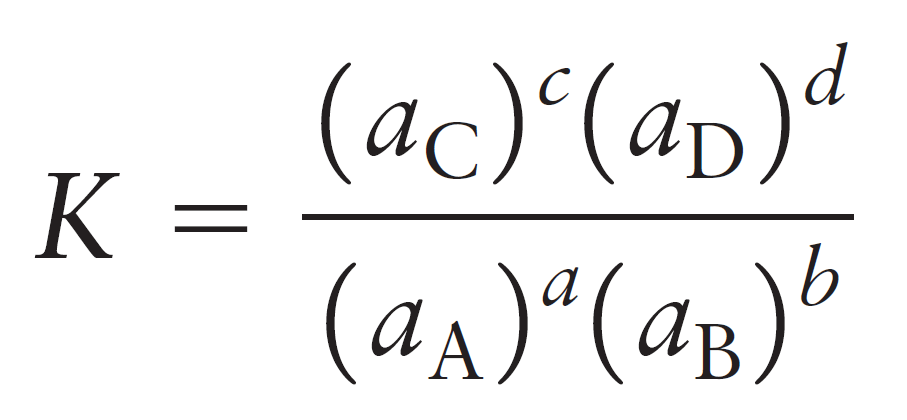
The activity of a substance in the solution is its molarity relative to the thermodynamic standard molarity c° which is equal to 1 mol/L and therefore, the units are canceled. For example, let’s say the equilibrium concentrations of NO2 and N2O4 gases are 0.0250 mol/l and 0.135 mol/l respectively:
N2O4(g) ⇆ 2NO2(g)
The equilibrium constant then is unitless and equals to:
\[{K_{\rm{c}}}\;{\rm{ = }}\;\frac{{{{\left[ {{\rm{N}}{{\rm{O}}_{\rm{2}}}} \right]}^2}}}{{\left[ {{{\rm{N}}_{\rm{2}}}{{\rm{O}}_4}} \right]}}\; = \;\frac{{{{\left( {\frac{{{\rm{0}}{\rm{.0250}}\;\cancel{{{\rm{mol/L}}}}}}{{{\rm{1}}\;\cancel{{{\rm{mol/L}}}}}}} \right)}^2}}}{{\left( {\frac{{{\rm{0}}{\rm{.0135}}\;\cancel{{{\rm{mol/L}}}}}}{{{\rm{1}}\;\cancel{{{\rm{mol/L}}}}}}} \right)}} = \,4.63\, \times \,{10^{ – 3}}\]
The difference in values of activities and molar concentrations may arise in real solutions, where intermolecular interactions are not insignificant because of higher concentrations. However, in undergraduate courses, you are going to use the molarity when working on equilibrium problems, so you don’t need to worry about this now.
The Equilibrium Constant and Extent of Reaction
The equilibrium constant measures how far the reaction proceeds, and therefore indicates whether the products or reactants are favored. In other words, it tells us whether there will be more products or reactants present in the solution once the equilibrium is established.
Because the reactants appear in the denominator of the equilibrium constant expression and products are in the numerator, a very large value of Kc means that the equilibrium mixture contains significantly more products than reactants. By contrast, if the reactants predominate in the mixture, the equilibrium constant is going to be a small number meaning that the reaction hardly proceeds.
As a reference, you can keep in mind that if K is much greater than 1 (K > 1), the equilibrium lies to the right and thus the products are favored. On the other hand, if the equilibrium constant is much smaller than 1 (K < 1), the equilibrium shifts to the left, and the reactants are favored.
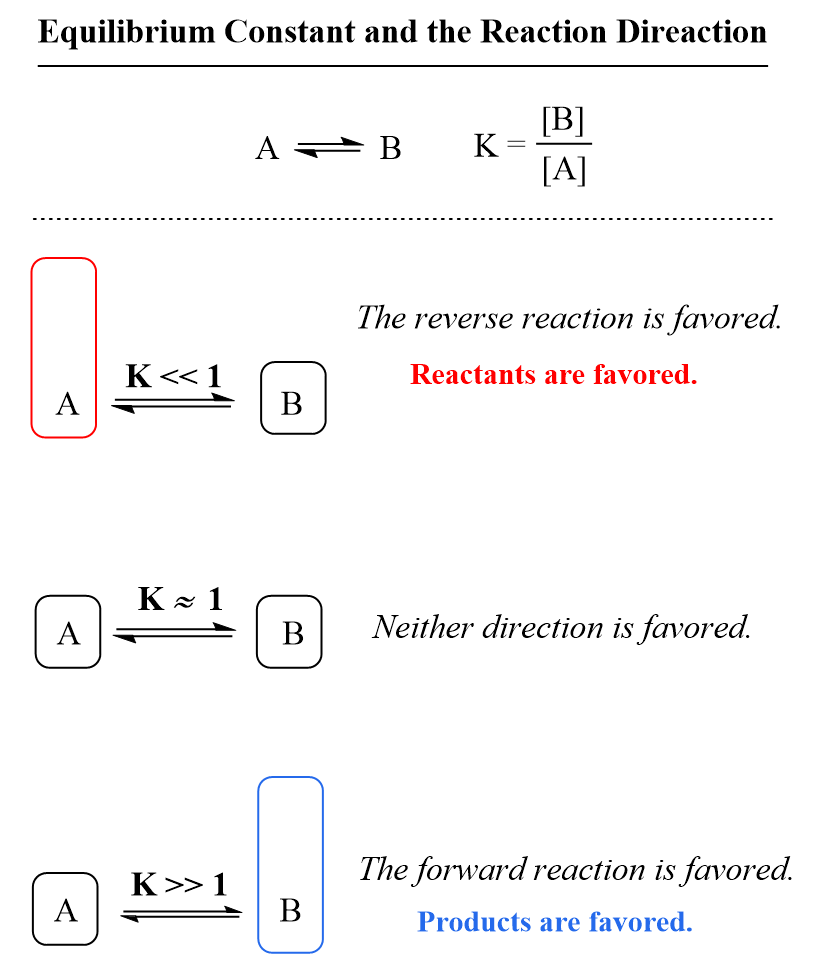
This is useful for predicting the outcome of a reaction when mixing reactants. For example, understanding the principle of equilibrium and values of equilibrium constant are very important for acid-base reactions in organic chemistry.
Homogenous and Heterogeneous Equilibria
You may have noticed that the examples above are all on reactions of gases. So, why is this important?
Well, first, it is worth mentioning that the very first studies and the observations about the ratio of the products and reactants leading to a constant number were made on reactions of gases.
These were done in 1864 by Norwegian mathematician Cato Guldberg and a chemist Peter Waage (you can read more about it here). They noticed that in a reaction between gas molecules, the ratio of the partial pressures of the products raised to the power of their coefficients over the product of the partial pressures of reactants raised to the power of their coefficients stays constant no matter what the initial concentrations were. This was how the pattern was observed and the expression for the equilibrium constant was derived.
For example, when sulfur dioxide was mixed with oxygen, it was found the following ratio of the partial pressures is always the same number
2SO2(g) + O2(g) ⇆ 2SO3(g)
\[{K_p} = \frac{{{P^2}_{{\rm{S}}{{\rm{O}}_{\rm{3}}}}}}{{{P^{\rm{2}}}{{_{{\rm{SO}}}}_{_2}}{P_{{{\rm{O}}_{\rm{2}}}}}}}\]
Where PSO3, PSO2, and PO2 are the partial pressure of the reaction components.
The subscript p on K is used to point out that the equilibrium constant Kp is defined using partial pressures.
We will discuss the relationship between Kc and Kp in a separate post.
The second point on emphasizing the state of the reactants and products is that we define homogenous and heterogeneous equilibria. Homogenous is the one where all the components are in the same phase such as, for example, reactions in solutions or between gases.
Heterogeneous equilibria are achieved in reactions where components are in different phases. For example, in the decomposition reaction of calcium carbonate, there are solids and a gas component present.
CaCO3(s) ⇆ CaO(s) + CO2(g)
The concentrations of pure solids and liquids present in a chemical equation are not included in the equilibrium constant expression. Therefore, the equilibrium constant for this reaction would be:
\[K = [C{O_2}]\]
The Kp can is written based on the partial pressure of carbon dioxide:
\[{K_{\rm{p}}} = {P_{C{O_2}}}\]
So, why do we omit the liquids and solids from the equilibrium constant?
Remember, we mentioned that the equilibrium constant is based on the activity of the components and not just their molarities and the activity of a pure solid or liquid is 1. This is because the
standard state for a pure liquid/solid is also the pure liquid/solid which gives a ratio of 1 and thus the activity is 1.
So, in for another example, the equilibrium constant for the oxidation of phosphorous P4 would be:
P4(s) + 5O2(g) ⇆ P4O10(s)
\[K = \frac{1}{{{{[{{\rm{O}}_2}]}^5}}}\]
\[{K_{\rm{p}}} = \frac{1}{{{P^5}_{{\rm{}}{{\rm{O}}_{\rm{2}}}}}}\]
Check Also
- Chemical Equilibrium
- Equilibrium Constant
- Kpand Partial Pressure
- Kp and KcRelationship
- K Changes with Chemical Equation
- Equilibrium Constant K from Two Reactions
- Reaction Quotient – Q
- ICE Table – Calculating Equilibrium Concentrations
- ICE Table Practice Problems
- Le Châtelier’s principle
- Le Châtelier’s principle Practice Problems
- Chemical Equilibrium Practice Problems

Great post!
Thank you!