Some reactions can be represented as a sequence of two or more relations. For example, let’s consider the following reaction between NOBr and Cl2 gases:
2NOBr(g) + Cl2(g) ⇆ 2NO(g) + 2 BrCl(g)
We can represent this net transformation as a sum of two reactions:
1) 2NOBr(g) ⇆ 2NO(g) + Br2(g)
2) Br2(g) + Cl2(g) ⇆ 2BrCl(g)
To confirm that these two give the target equation, simply add them up and cancel out the identical components on both sides of the equation:
1) 2NOBr(g) ⇆ 2NO(g) + Br2(g)
+
2) Br2(g) + Cl2(g) ⇆ 2BrCl(g)
2NOBr(g) + Br2(g) + Cl2(g) ⇆ 2NO(g) + Br2(g) + 2 BrCl(g)
_______________________________________________
3) 2NOBr(g) + Cl2(g) ⇆ 2NO(g) + 2 BrCl(g)
So, Br2 appeared on both sides of the equation and by canceling it, we obtained the final equation (3).
Now, how is this related to the equilibrium constant?
It turns out that we can calculate the equilibrium constant for a reaction if we know the equilibrium constants for other reactions that add up to this reaction. For this, you simply need to multiply the equilibrium constants of the two reactions.
For example, suppose the equilibrium constants of reactions (1) and (2) are 0.012 and 7.2 respectively:
1) 2NOBr(g) ⇆ 2NO(g) + Br2(g)
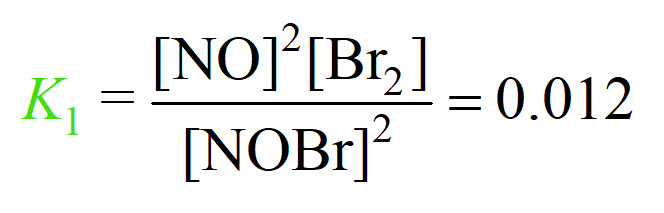
2) Br2(g) + Cl2(g) ⇆ 2BrCl(g)
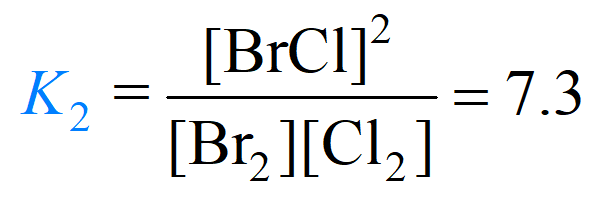
To obtain the equilibrium constant for reaction (3), we multiply the ones for reaction (1) and (2):
2NOBr(g) + Cl2(g) ⇆ 2NO(g) + 2BrCl(g) (3)
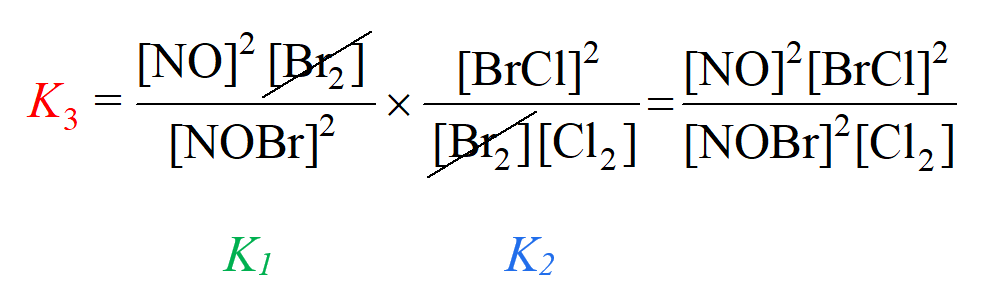
Notice that we got an expression for K3 that matches what we’d write according to the chemical equation (3).
Therefore, the value of K3 is the product of K1 and K2:
K3 = K1 x K2 = 0.012 x 7.3 = 0.088
If this is confusing, you can review the Hess’s law which uses a similar strategy to calculate the enthalpy of a reaction based on the enthalpy of other reactions that add up to it.
Practice
The equilibrium constant values for the reactions below were determined at a certain temperature:
S(s) + O2(g) ⇆ SO2(g) Ka = 3.2 x 1045
2S(s) + 3O2(g) ⇆ 2SO3(g) Kb = 3.2 x 10124
Using these data, determine the equilibrium constant Kc for the following reaction:
2SO2(g) + O2(g) ⇆ 2SO3(g) Kc = ?
The equilibrium constant values for the reactions below were determined at a certain temperature:
2NO(g) ⇆ N2(g) + O2(g) Ka = 3.8 x 1032
NO(g) + 1/2Cl2(g) ⇆ NOCl(g) Kb = 6.4
Using these data, determine the equilibrium constant Kc for the following reaction:
1/2N2(g) + 1/2O2(g) + 1/2Cl2(g) ⇆ NOCl(g) Kc = ?
Check Also
- Chemical Equilibrium
- Equilibrium Constant
- Kpand Partial Pressure
- Kp and KcRelationship
- K Changes with Chemical Equation
- Equilibrium Constant K from Two Reactions
- Reaction Quotient – Q
- ICE Table – Calculating Equilibrium Concentrations
- ICE Table Practice Problems
- Le Châtelier’s principle
- Le Châtelier’s principle Practice Problems
- Chemical Equilibrium Practice Problems
