The first studies and the observations of patterns in the ratio of the products and reactants were made in 1864 by Norwegian mathematician Cato Guldberg and a chemist Peter Waage when working on reactions of gases.

They noticed that in a reaction between gas molecules, the ratio of the partial pressures of the products over the product of the partial pressures of reactants raised to the power of their coefficients stays constant no matter what the initial amounts of were. This was how the expression for the equilibrium constant was derived.

For example, when sulfur dioxide was mixed with oxygen, it was found the following ratio of the partial pressures is always the same number:

2SO₂(g) + O₂(g) ⇆ 2SO₃(g)

\[{K_p} = \frac{{{P^2}_{{\rm{S}}{{\rm{O}}_{\rm{3}}}}}}{{{P^{\rm{2}}}{{_{{\rm{SO}}}}_{_2}}{P_{{{\rm{O}}_{\rm{2}}}}}}}\]

Where PSO₃, PSO₂, and PO₂ are the partial pressure of the reaction components.

The subscript p on K is used to point out that the equilibrium constant Kp is defined using partial pressures.

The equilibrium constant can also be expressed in terms of the molar concentrations:

\[{K_c} = \frac{{{{\left[ {{\rm{S}}{{\rm{O}}_{\rm{3}}}} \right]}^2}}}{{{{\left[ {{\rm{S}}{{\rm{O}}_{\rm{2}}}} \right]}^2}\left[ {{{\rm{O}}_{\rm{2}}}} \right]}}\]

The values of K_p and K_c are often different, however, we can calculate one from the other based on the coefficients of the balanced chemical equation. We will cover this in the next article.

For a general reaction of gases, the equilibrium constant K_p can be represented as:

aA + bB ⇆ cC + dD

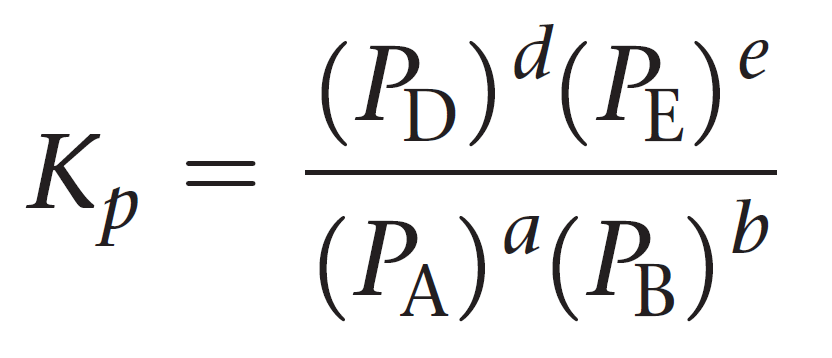
Let’s see an example of calculating K_p.

As for the K_c, the expression and value of K_p depend on the chemical equation, mainly the coefficients and the direction of the reaction.

Let’s see how these are related.

Kp for the reverse reaction

The following reaction has an equilibrium constant of K_p = 4.42 x 10^-5 at 298 K:

CH₃OH(g) ⇆ CO(g) + 2H₂(g)

Calculate the equilibrium constant for this process if the reaction is represented as follows:

 CO(g) + 2H₂(g) ⇆ CH₃OH(g)

Remember, when a reaction is reversed, then K_new = 1/K_original.

Therefore, 

K_new = 1/K_original= 1/4.42 x 10^-5= 22,624.43 = 2.26 x 10⁴

Kp When the Coefficients are Changed

Based on the K_p value given above, what is the K_p for the following reaction?

2CH₃OH(g) ⇆ 2CO(g) + 4H₂(g)

Comparing this equation to the original, we see that it is multiplied by 2. Remember when the coefficients in the equation are multiplied by any factor, we raise the equilibrium constant to the same factor. Therefore, 

K_new = (K_original)ⁿ = (4.42 x 10^-5)²= 1.96 x 10^-9