This equilibrium practice problem set includes questions on writing the equilibrium constant of given chemical reactions, determining the value of the equilibrium constant based on the concentrations and partial pressures of gases, deriving a new expression for an equilibrium constant from separate reactions, converting between Kc and Kp, calculating the quotient and determining the course of the reaction, calculations of concentrations based on the quotient and equilibrium constant, as well as working on equilibrium reactions based on the Le Châtelier’s principle.
The links to the corresponding articles are provided herein:
- Chemical Equilibrium
- Equilibrium Constant
- Kpand Partial Pressure
- Kp and KcRelationship
- K Changes with Chemical Equation
- Equilibrium Constant K from Two Reactions
- Reaction Quotient – Q
- ICE Table – Calculating Equilibrium Concentrations
- ICE Table Practice Problems
- Le Châtelier’s principle
- Le Châtelier’s principle Practice Problems
- Chemical Equilibrium Practice Problems
Practice
Write the equilibrium expression (K) for each of the following reactions.
A) N2(g) + O2(g) ⇆ 2NO(g)
B) 2NOCl(g) ⇆ 2NO(g) + Cl2(g)
C) CH3COOH(aq) ⇆ H+(aq) + CH3COO2–(aq)
D) 2CuS(s) + 3O2(g) ⇆ 2CuO(s) + 2SO2(g)
E) CO2(g) + 3H2(g) ⇆ CH3OH(g) + H2O(g)
F) 2SO3(g) ⇆ 2SO2(g) + O2(g)
G) CaCO3(s) ⇆ CaO(s) + CO2(g)
H) Fe2O3(s) + 3CO(g) ⇆ 2Fe(s) + 3CO2(g)
I) 4HCl(g) + O2(g) ⇆ 2Cl2(g) + 2H2O(g)
J) CO32-(aq) + H2O(l) ⇆ HCO3–(aq) + OH–(aq)
K) P4(s) + 5O2(g) ⇆ P4O10(s)
l) 2H+(aq) + Zn(s) ⇆ H2(g) + Zn2+(aq)
Tree different reactions are represented in the diagram below. The reaction equations can be written as A + X ⇆ AX (X = B, C, or D).
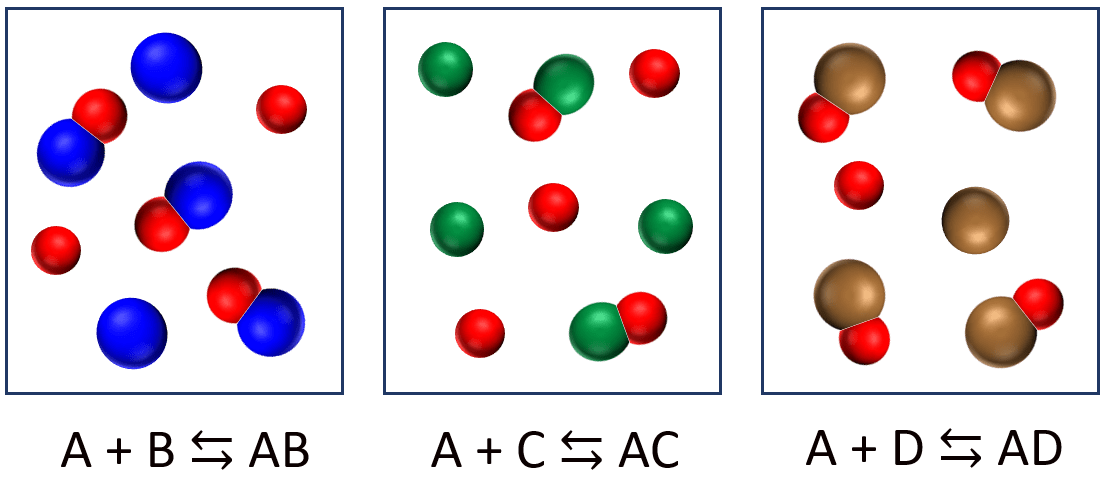
(a) Which reaction has the largest equilibrium constant? (b) Which reaction has the smallest equilibrium constant?
The following graph represents an initial mixture of N2 and H2 at high temperature and pressure:
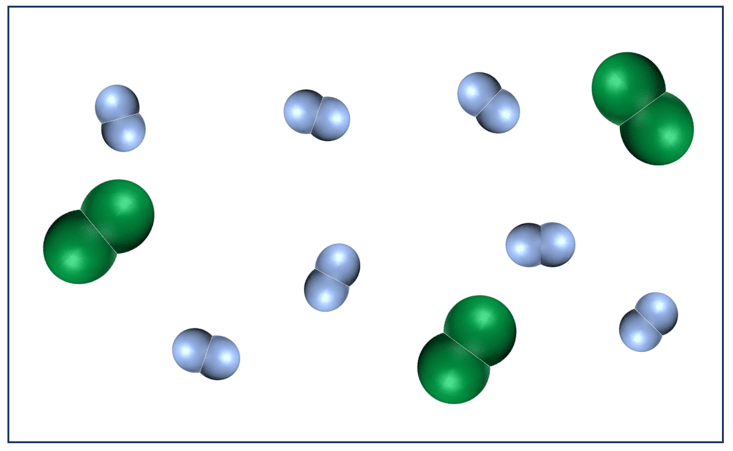
The gases react to form ammonia gas (NH3) as represented by the following concentration profile:

a) Label each plot on the graph as H2, N2, or NH3, and explain your answers.
b) What information do the relative shapes of the plots tell us?
c) At what time is equilibrium reached?
At a particular temperature, it is determined for the reaction
2NO(g) + 2H2(g) ⇆ N2 (g) + 2H2O(g)
that at equilibrium, the concentrations are as follows: [NO(g)] = 3.2 x 10-3 M, [H2(g)] = 6.7 x 10-6 M, [N2(g)] = 4.8 x 10-2 M, and [H2O(g)] = 2.4 x 10-2 M. What is the value of the equilibrium constant K for the reaction at this temperature?
Given the equilibrium concentrations, calculate the value of the equilibrium constant K for the reaction between CO2 and H2 that produces methanol and water at high temperature.
CO2(g) + 3H2(g) ⇆ CH3OH(g) + H2O(g)
[CO2] = 0.061 M, [H2] = 0.079 M, [CH3OH] = 4.7 x 102 M, and [H2O] = 5.7 x 104 M Calculate the value of K for the reaction.
The reaction for converting methane to acetylene has an equilibrium constant of K = 0.154 at 2000 K.
2CH4(g) ⇆ C2H2(g) + 3H2(g)
Calculate the equilibrium constant for this process if the reaction is represented as follows:
a) CH4(g) ⇆ 1/2C2H2(g) + 3/2H2(g)
b) 4CH4(g) ⇆ 2C2H2(g) + 6H2(g)
c) 6CH4(g) ⇆ 3C2H2(g) + 9H2(g)
The following reaction has an equilibrium constant of Kp = 4.42 x 10-5 at 298 K:
CH3OH(g) ⇆ CO (g) + 2H2(g)
Calculate the equilibrium constant for this process if the reaction is represented as follows:
a) CO(g) + 2H2(g) ⇆ CH3OH(g)
b) 2CH3OH(g) ⇆ 2CO(g) + 4H2(g)
c) 1/2CH3OH(g) ⇆ 1/2CO(g) + H2(g)
The equilibrium constant values for the reactions below were determined at a certain temperature:
S(s) + O2(g) ⇆ SO2(g) Ka = 3.2 x 1045
2S(s) + 3O2(g) ⇆ 2SO3(g) Kb = 3.2 x 10124
Using these data, determine the equilibrium constant Kc for the following reaction:
2SO2(g) + O2(g) ⇆ 2SO3(g) Kc = ?
The equilibrium constant values for the reactions below were determined at a certain temperature:
2NO(g) ⇆ N2(g) + O2(g) Ka = 3.8 x 1032
NO(g) + 1/2Cl2(g) ⇆ NOCl(g) Kb = 6.4
Using these data, determine the equilibrium constant Kc for the following reaction:
1/2N2(g) + 1/2O2(g) + 1/2Cl2(g) ⇆ NOCl(g) Kc = ?
The following equilibrium pressures were observed at a certain temperature for the Haber process
3H2(g) + N2(g) ⇆ 2NH3(g)
P(NH3) = 5.2 x 109 atm
P(N2) = 6.1 x 102 atm
P(H2) = 4.7 x 103 atm
Calculate the value for the equilibrium constant Kp at this temperature.
Consider the following reactions:
1) H2(g) + I2(g) ⇆ 2HI(g)
2) H2(g) + I2(s) ⇆ 2HI(g)
In which reaction are the K and Kp equal?
At 300 K, the equilibrium concentrations for the following reaction are [CH3OH] = 0.240 M, [CO] = 0.350 M, and [H2] = 1.65 M for the reaction
CH3OH(g) ⇆ CO(g) + 2H2(g)
Calculate Kp at this temperature.
Given the equilibrium constant, calculate Kp for each of the following reactions at 298 K.
a) N2O4(g) ⇆ 2NO2(g) Kc = 4.6 x 10-4
b) 3H2(g) + N2(g) ⇆ 2NH3(g) Kc = 6.7 x 109
c) H2(g) + B2(g) ⇆ 2HBr(g) Kc = 5.20 x 1018
Calculate the Kc for each reaction at 298 K.
a) CO(g) + Cl2(g) ⇆ COCl2(g) Kp = 5.3 x 106
b) CH4(g) + H2O(g) ⇆ CO(g) + 3H2(g) Kp = 7.7 x 108
c) 2SO2(g) + O2(g) ⇆ 2SO3(g) Kp = 6.26 x 105
Consider the reaction between nitrogen and hydrogen gases:
3H2(g) + N2(g) ⇆ 2NH3(g)
Using the data given in the table, complete the missing numbers assuming that all concentrations are measured at equilibrium.
| Temp | [N2] | [H2] | [NH3] | K |
| 400 | 0.142 | 0.129 | 0.518 | ? |
| 600 | 0.125 | 0.116 | ? | 7.8 |
| 850 | 0.136 | ? | 0.712 | 0.0647 |
Consider the following reaction at 298 K:
2NO(g) + Cl2(g) ⇆ 2NOCl(g) Kp = 31.6
In a reaction mixture at equilibrium, the partial pressure of NO is 128 torr and that of Cl2 is 176 torr. Calculate the partial pressure of NOCl at equilibrium.
The equilibrium constant for the following reaction at 600 oC is determined to be Kc = 0.495:
H2O(g) + CO(g) ⇆ H2(g) + CO2(g)
Calculate the number of H2 moles that are present at equilibrium if a mixture of 0.400 mole CO and 0.500 mole H2O is heated to 600°C in a 10.0-L container.
The equilibrium constant Kc for the following reaction at 800°C is 3.74 x 105
H2(g) + I2(g) ⇆ 2HI(g)
If 6.25 moles of HI were initially added to a 15.0-L empty vessel, what would the concentrations of H2, I2, and HI be at equilibrium.
The equilibrium constant for the following reaction at 700 K is Kp = 6.7 x 10-3
CO(g) + 2H2(g) ⇆ CH3OH(g)
A reaction mixture contains 0.248 atm of H2, 0.085 atm of CO, and 0.598 atm of CH3OH. Is the reaction mixture at equilibrium? If not, in what direction will the reaction proceed?
For the reaction shown below, Kc = 0.654 at 600 K.
N2O4(g) ⇆ 2NO2(g)
If initially, 0.0600 M of N2O4 are present in the reaction vessel, what are the equilibrium concentrations of the gases at 600 K?
For the reaction shown below, Kc = 255 at 800 K.
PCl3(g) + Cl2(g) ⇆ PCl5(g)
If a reaction mixture initially contains 0.3500 M PCl3 and 0.375 M Cl2 at 800 K, what are the equilibrium concentrations of all the species in the mixture?
Consider the following reaction characterized with Kp = 2.34 x 10-4 at 250 K:
I2(g) + Cl2(g) ⇆ 2ICl(g)
A reaction mixture initially contains I2 with partial pressure of 655 torr and Cl2 with partial pressure of 864 torr at 250 K. Calculate the equilibrium partial pressure of ICl.
Consider the following reversible reaction:
POCl3(g) ⇌ POCl(g) + Cl2(g) Kc = 0.650
The following initial amounts of reactants and products were mixed: [POCl3] = 0.650 M, [POCl] = 0.450 M, and [Cl2] = 0.250 M.
Calculate the reaction quotient, Qc, and determine the equilibrium concentration of POCl?
Consider the following equilibrium:
2NO(g) + 2H2(g) ⇆ N2(g) + 2H2O(g)
Initially, there are 0.15 moles of NO and 0.25 moles of H2, in a 10.0-L container. If there are 0.056 moles of NO at equilibrium, how many moles of N2 are present at equilibrium?
Consider the following equilibrium:
2NOCl(g) ⇆ 2NO(g) + Cl2(g)
2.00 mole of pure NOCl and 1.65 mole of pure Cl2 are placed in a 1.00-L container. Calculate the equilibrium concentration of NO(g) considering that with K = 2.4 x 10–6.
Consider the following equilibrium process
2SO3(g) ⇆ 2SO2(g) + O2(g) ΔH° = 2198 kJ/mol
How will the concentrations of SO2, O2, and SO3 be affected in each scenario?
(a) the temperature is increased
(b) the pressure is decreased by increasing the volume of the container
(c) the concentration of O2 is increased
(d) a is added catalyst
(e) an inert gas is added at constant volume
Suppose you need to increase the amount of C3H6Cl2 produced in the following exothermic reaction:
C3H6(g) + Cl2(g) ⇆ C3H6Cl2(g)
Which of the following strategies will work once the reaction mixture reaches equilibrium?
a) decreasing the reaction volume
b) removing C3H6Cl2 from the reaction mixture as it forms
c) adding a catalyst
d) adding Cl2
e) increasing the temperature
Predict the shift in the equilibrium position that will occur for each of the following reactions at equilibrium when the volume of the reaction container is increased.
1) PCl3(g) + Cl2(g) ⇆ PCl5(g)
2) 2NBr3(g) ⇆ N2(g) + 3Br2(g)
3) CO(g) + Cl2(g) ⇆ COCl2(g)
4) H2(g) + B2(g) ⇆ 2HBr(g)
5) MgCO3(s) ⇆ MgO(s) + CO2(g)
Consider the following equilibrium process for the commercial production of hydrogen:
CO(g) + H2O(g) ⇆ CO2(g) + H2(g) ΔH° = +42 kJ/mol
Predict the direction of the shift in equilibrium when
(a) the temperature is raised.
(b) more CO gas is added to the reaction mixture.
(c) some CO2 is removed from the mixture.
(d) the pressure on the gases is increased by changing the volume of the container.
(e) a catalyst is added to the reaction mixture
Consider this reaction at equilibrium:
N2 + O2(g) ⇆ 2NO(g)
Predict whether the reaction will shift left, shift right, or remain unchanged after each disturbance.
a) NO is added to the reaction mixture.
b) N2 is added to the reaction mixture.
c) NO is removed from the reaction mixture.


it is very helpful
Glad to hear that. Thanks.