We mentioned in the previous post that the equilibrium-constant expression can be formulated in terms of partial pressures when the reactants and products in a chemical reaction are gases.

For example, when the equilibrium constant of the reaction between sulfur dioxide and oxygen, can be expressed based on the molar concentrations (K_c) or the partial pressures (K_p):

2SO₂(g) + O₂(g) ⇆ 2SO₃(g)

\[{K_c} = \frac{{{{\left[ {{\rm{S}}{{\rm{O}}_{\rm{3}}}} \right]}^2}}}{{{{\left[ {{\rm{S}}{{\rm{O}}_{\rm{2}}}} \right]}^2}\left[ {{{\rm{O}}_{\rm{2}}}} \right]}}\]

\[{K_p} = \frac{{{P^2}_{{\rm{S}}{{\rm{O}}_{\rm{3}}}}}}{{{P^{\rm{2}}}{{_{{\rm{SO}}}}_{_2}}{P_{{{\rm{O}}_{\rm{2}}}}}}}\]

Where PSO₃, PSO₂, and PO₂ are the partial pressure of the reaction components.

The subscript p on K is used to point out that the equilibrium constant K_p is defined using partial pressures.

For a general reaction of gases, the equilibrium constant K_p can be represented as:

aA + bB ⇆ cC + dD

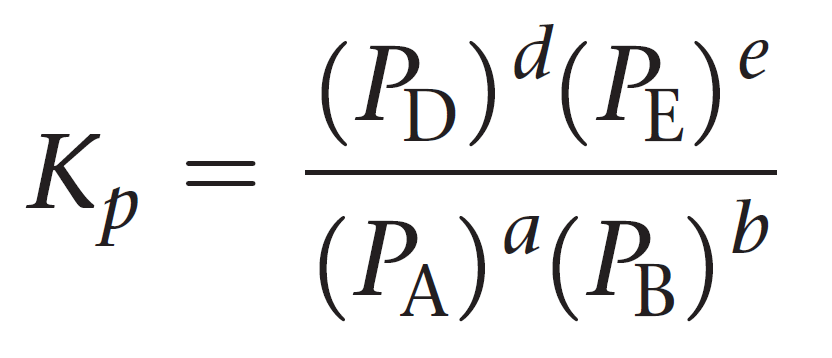
Let’s see an example of calculating K_p.

The Relationship Between K_p and K_c

Although the values of K_p and K_c are generally different, it is possible to calculate one from the other using the ideal gas law equation. The idea is to rearrange the ideal gas law equation to get an expression for the partial pressure of each gas and use in the equation of K_p.

PV = nRT, so for P, we can write:

\[P\; = \;\frac{n}{V}RT\]

Remember that n/V is the molarity, so the partial pressure of gas “A” is equal to:

\[{P_A}\; = \;\frac{{{n_A}}}{V}RT\; = \,\left[ {\rm{A}} \right]RT\]

The equivalent expression for the partial pressure of each gas is then entered in the equation of K_p:

This expression is then simplified by separating the terms of concentration and RT:

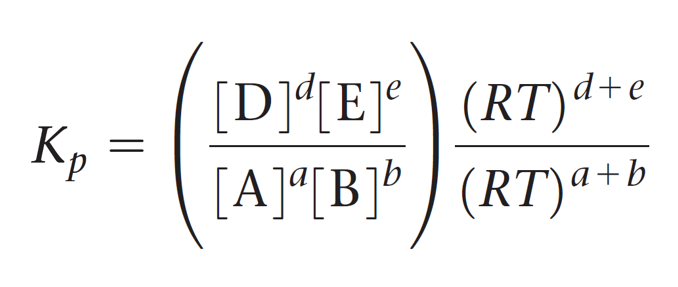
And now the cool part; Notice that the term in brackets on the left side is equal to Kc, so we can further simplify this expression:

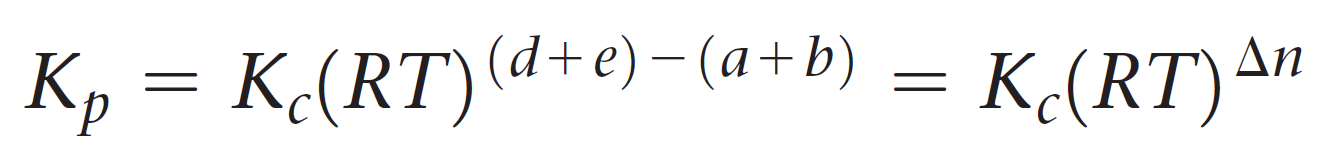
Let’s put this as separate formula correlating Kp and Kc since you are going to use it quite often when solving equilibrium problems:

aA + bB ⇆ cC + dD

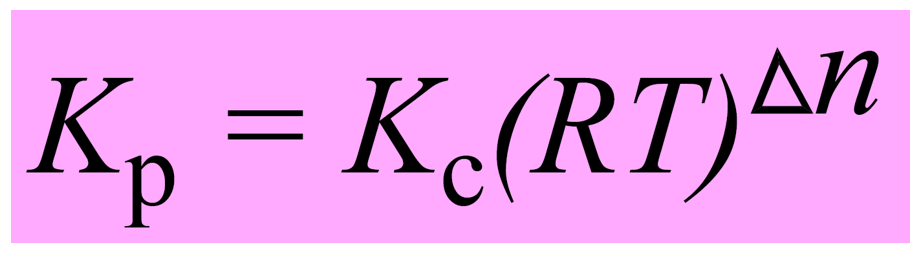
The quantity Δn is the number of moles of gaseous products minus the number of moles of gaseous reactants.

Δn = (c + d) – (a + b)

R is the gas constant, 0.08206 (L · atm)/ (K · mol) , and T is the absolute temperature in Kelvins.

When the number of products and reactant molecules is equal, then K_c = K_p because K_p = K(RT)⁰ = K.

For example, suppose the K_c of the reaction between hydrogen and bromine gases is 5.20 x 10^18.

H₂(g) + B₂(g) ⇆ 2HBr(g) K_c = 5.20 x 10¹⁸

Determine the K_p of this reaction.

Solution: K_p = K(RT)⁰ = K = 5.20 x 10¹⁸

Kp Changes with Chemical Equation

The expression of Kp changes with the chemical equation just like we saw it for Kc.

Kp for the reverse reaction

The following reaction has an equilibrium constant of K_p = 4.42 x 10^-5 at 298 K:

CH₃OH(g) ⇆ CO(g) + 2H₂(g)

Calculate the equilibrium constant for this process if the reaction is represented as follows:

 CO(g) + 2H₂(g) ⇆ CH₃OH(g)

Remember, when a reaction is reversed, then K_new = 1/K_original.

Therefore, 

K_new = 1/K_original= 1/4.42 x 10^-5= 22,624.43 = 2.26 x 10⁴

Kp When the Coefficients are Changed

Based on the Kp value given above, what is the Kp for the following reaction?

2CH₃OH(g) ⇆ 2CO(g) + 4H₂(g)

Comparing this equation to the original, we see that it is multiplied by 2. Remember when the coefficients in the equation are multiplied by any factor, we raise the equilibrium constant to the same factor. Therefore, 

K_new = (K_original)ⁿ = (4.42 x 10^-5)²= 1.96 x 10^-9