To understand the partial pressures, let’s suppose a certain amount of gas “A” is added to the tank and extorts 5 atm pressure, and in another tank with gas “B” the pressure is 3 atm:

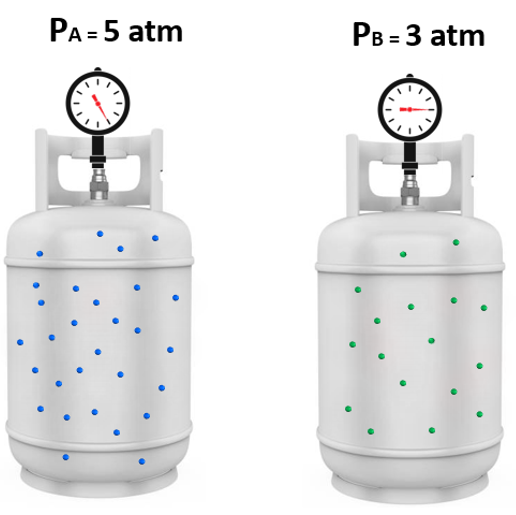
Now, it turns out that if we mix these amounts of gas A and B together, the total pressure is 8 atm. And this intuitive observation was first formulated by John Dalton and is known as the Dalton’s law of partial pressures.

It states that the total pressure of a gas mixture is equal to the sum of the pressures that each gas would exert if it were present alone:

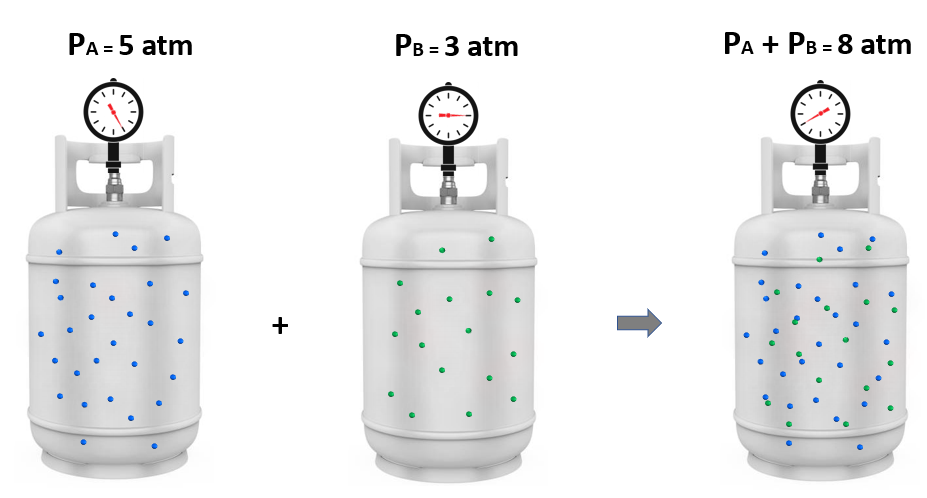
 The individual pressure of each gas component is called a partial pressure, so the total pressure is the sum of the partial pressures:

P_Total = P_A + P_B

This formula is true for any number of gas types in the, and in a more general way, we can write:

P_Total = P₁ + P₂ + … + Pn

For example,

What is the partial pressure of nitrogen in a mixture of N₂, SO₂ and CO₂ that has a total pressure of 6.84 atm. The partial pressure of SO₂ is 2.10 atm, and the partial pressure of CO₂ is 1.74 atm.

The total pressure is the sum of the partial pressures of all the gasses in the mixture:

P_T = P(N₂) + P(SO₂) + P(CO₂) = 6.84 atm

P(N₂) = P_T – [P(SO₂) + P(CO₂)]

P(N₂) = 6.84 atm – [2.10 atm + 1.74 atm]

P(N₂) = 3.00 atm

Another example,

13.2 grams of CO₂ and 6.00 grams of He are mixed in a 4.00 L container at 300. K. Calculate the partial pressure of both gases and the total pressure of the mixture.

First, we need to determine the moles of the gases using the ideal gas law equation:

\[{\rm{P}}\;{\rm{ = }}\;\frac{{{\rm{nRT}}}}{{\rm{V}}}\]

\[{\rm{P}}\;{\rm{(C}}{{\rm{O}}_{\rm{2}}}{\rm{)}}\;{\rm{ = }}\;\frac{{{\rm{nRT}}}}{{\rm{V}}}\]

\[{\rm{P}}\;{\rm{(C}}{{\rm{O}}_{\rm{2}}}{\rm{)}}\;{\rm{ = }}\;\frac{{{\rm{0}}{\rm{.300}}\;\cancel{{{\rm{mol}}}}{\rm{  \times }}\;{\rm{0}}{\rm{.08206}}\;\cancel{{\rm{L}}}\;{\rm{atm}}\;\cancel{{{{\rm{K}}^{{\rm{ – 1}}}}}}\;{\rm{mo}}{{\rm{l}}^{{\rm{ – 1}}}}\;{\rm{300}}{\rm{.}}\;\cancel{{\rm{K}}}}}{{{\rm{4}}{\rm{.00}}\;\cancel{{\rm{L}}}}}\; = \;{\rm{1}}{\rm{.85}}\;{\rm{atm}}\]

\[{\rm{P}}\;{\rm{(He)}}\;{\rm{ = }}\;\frac{{{\rm{1}}{\rm{.50}}\;\cancel{{{\rm{mol}}}}{\rm{  \times }}\;{\rm{0}}{\rm{.08206}}\;\cancel{{\rm{L}}}\;{\rm{atm}}\;\cancel{{{{\rm{K}}^{{\rm{ – 1}}}}}}\;{\rm{mo}}{{\rm{l}}^{{\rm{ – 1}}}}\;{\rm{300}}{\rm{.}}\;\cancel{{\rm{K}}}}}{{{\rm{4}}{\rm{.00}}\;\cancel{{\rm{L}}}}}\; = \;{\rm{9}}{\rm{.23}}\;{\rm{atm}}\]

These are the partial pressure of CO₂ and He, so to find the total pressure, we add them up:

P_total = 1.85 + 9.23 = 11.1 atm

Check Also

• Ideal-Gas Laws
• Combined Gas Law Equation
• How to Know Which Gas Law Equation to Use
• Molar Mass and Density of Gases
• Graham’s Law of Effusion and Diffusion
• Mole Fraction and Partial Pressure of the Gas
• Gases in Chemical Reactions
• Gases – Practice Problems