In the previous post, we talked about the Graham’s law which shows that the rate of effusion of a gas is inversely proportional to the square root of its molar mass:
\[{u_{{\rm{rms}}}}\;{\rm{ = }}\;\sqrt {\frac{{{\rm{3RT}}}}{{\rm{M}}}} \]
One application of Graham’s law is the formula obtained for two gases correlating their molar masses and effusion rates:
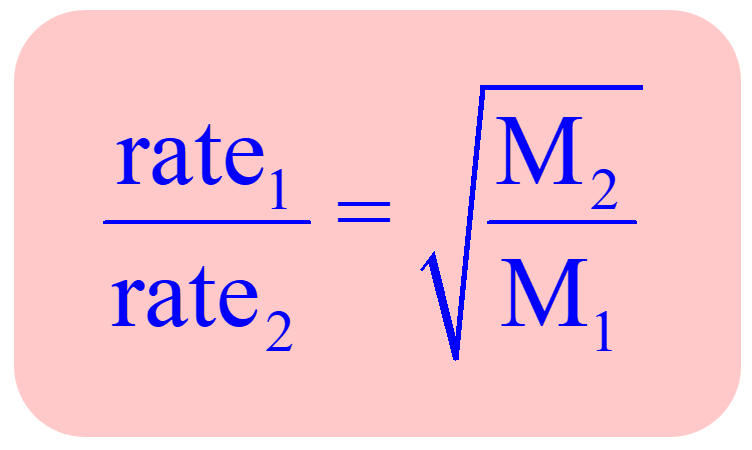
This allows for determining the molar mass of unknown gas by comparing its effusion rate to standard gas.
Below are some practice examples of the Graham’s law of effusion:
Check Also
Practice
What is the ratio of the effusion rates of hydrogen gas (H2) and carbon dioxide (CO2) at the same pressure and temperature?
The rate of effusion of an unknown gas is 9.20 mL/min. Under identical conditions, the rate of effusion of pure nitrogen (N2) gas is 14.65 mL/min. Identify the unknown gas using the Graham’s law.
a) O2 b) C3H8 c) C4H10 d) NO2 e) Cl2
A sample of krypton effuses from a container in 95 seconds. The same amount of an unknown gas requires 55 seconds. Identify the unknown gas.
If a sample of Br2 vapor can effuse from an opening in a heated vessel in 46 s, how long will it take the same amount of He to effuse under identical conditions?
It has been demonstrated that 3.56 mL of an unknown gas effuses through a hole in the same time that 8.64 mL of argon does under the same conditions. Determine the molecular mass of the unknown gas.
