The mixing of different gas molecules by random molecular motion and frequent collisions is called diffusion.
An example of this can be the raid odor spread of perfume when the stopper is removed.
Effusion is a similar process in which gas molecules escape without collisions through a tiny hole into a vacuum.
Both the diffusion and effusion occur at different rates depending on the gas, Mainly, the size of the gas particles. As expected, the smaller the particles, the faster they effuse and defuse.
This was studied and formulated by a Scottish chemist Thomas Graham who found that the rate of effusion of a gas is inversely proportional to the square root of its molar mass:
\[{u_{{\rm{rms}}}}\;{\rm{ = }}\;\sqrt {\frac{{{\rm{3RT}}}}{{\rm{M}}}} \]
This shows mathematically how the lighter molecule will effuse rapidly compared to a heavier one. Combining this correlation for two gases, a practical application of the Graham’s law is obtained which can be used in effusion experiments of a known gas and an unknown gas for determining its molar mass:
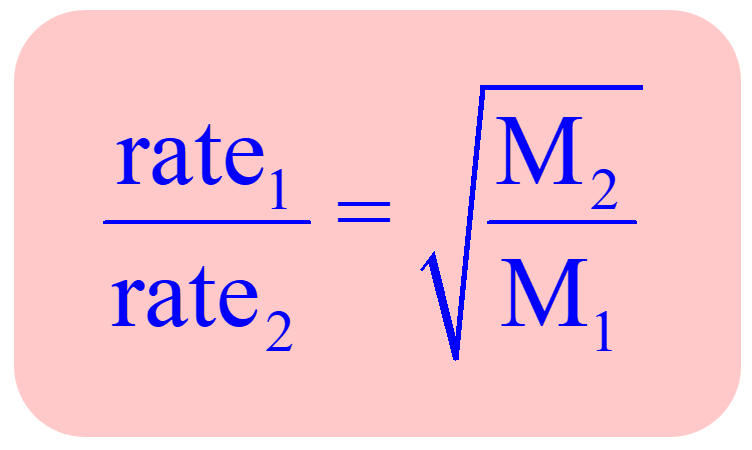
For example,
The rate of effusion of an unknown gas is 9.20 mL/min. Under identical conditions, the rate of effusion of pure nitrogen (N2) gas is 14.65 mL/min. Identify the unknown gas using the Graham’s law.
a) O2 b) C3H8 c) C4H10 d) NO2 e) Cl2
\[\frac{{{\rm{rate}}\;{\rm{X}}}}{{{\rm{rate}}\;{{\rm{N}}_{\rm{2}}}}}\;{\rm{ = }}\;\sqrt {\frac{{{{\rm{M}}_{{{\rm{N}}_{\rm{2}}}}}}}{{{{\rm{M}}_{\rm{X}}}}}} \]
You can square both sides of the equation to get rid of the square root:
\[{\left( {\frac{{{\rm{rate}}\;{\rm{X}}}}{{{\rm{rate}}\;{{\rm{N}}_{\rm{2}}}}}} \right)^2}\;{\rm{ = }}\;\frac{{{{\rm{M}}_{{{\rm{N}}_{\rm{2}}}}}}}{{{{\rm{M}}_{\rm{X}}}}}\]
Next, rearrange the equation to get an expression for the molar of the unknown gas (Mx):
\[{{\rm{M}}_{\rm{X}}}\; = \,\frac{{{{\rm{M}}_{{{\rm{N}}_{\rm{2}}}}}}}{{{{\left( {\frac{{{\rm{rate}}\;{\rm{X}}}}{{{\rm{rate}}\;{{\rm{N}}_{\rm{2}}}}}} \right)}^2}}}\]
\[{{\rm{M}}_{\rm{X}}}\; = \,\frac{{{\rm{28}}{\rm{.0}}\;{\rm{g/mol}}}}{{{{\left( {\frac{{{\rm{9}}{\rm{.20}}\;{\rm{mL/min}}}}{{{\rm{14}}{\rm{.65}}\;{\rm{mL/min}}}}} \right)}^{\rm{2}}}}}\;{\rm{ = }}\;{\rm{71}}{\rm{.0}}\;{\rm{g/mol}}\]
The molar mass of the unknown gas is 71 g/mol, and therefore, it is chlorine.
Check Also
Practice
What is the ratio of the effusion rates of hydrogen gas (H2) and carbon dioxide (CO2) at the same pressure and temperature?
The rate of effusion of an unknown gas is 9.20 mL/min. Under identical conditions, the rate of effusion of pure nitrogen (N2) gas is 14.65 mL/min. Identify the unknown gas using the Graham’s law.
a) O2 b) C3H8 c) C4H10 d) NO2 e) Cl2
