In the previous post, we talked about partial pressures and the Dalton law. Today, we will see how the mole fraction and partial pressures of a gas are related.

Remember, mole fraction (Χ) is the ratio of the moles of a component over the total number of moles of all the components.

 

 

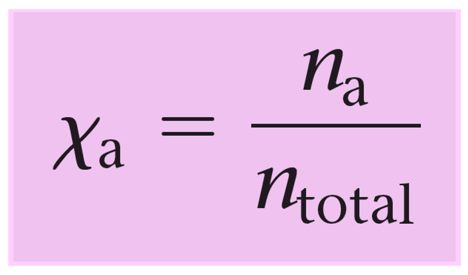
So, we can visualize this as the percentage of a gas in a mixture which helps quickly determine its partial pressure.

For example, say take mixture of gases containing 60% of gas “A” and 40% of gas “B” and the total pressure is 10 atm.

What is the partial pressure of each gas in the mixture?

 

 

You may have already determined that the partial pressure of A and B are 6 atm and 4 atm. We get these numbers by multiplying the total pressure with the corresponding fraction of each gas. So, for gas A, it is:

 

0.6 x 10 atm = 6 atm

 

and for gas B, it is:

 

0.4 x 10 atm = 4 atm

  

These fractions (0.6 and 0.4) are the mole fractions of gas A and B. Now, while this calculation is straightforward because of the whole numbers, there are cases, where a general formula is needed, and the formula shows that the partial pressure of a gas is equal to the product of its mole fraction and the total pressure:

 

 

For example,

A mixture of gases contains CH₄, N₂, and H₂ and exerts a total pressure of 2.65 atm. The mixture contains 0.456 mol of CH₄, 0.540 mol of N₂ and 0.730 mol of H₂. What is the partial pressure of hydrogen in atmospheres?

We first write the formula for the partial pressure of hydrogen:

 

P(H₂) = χ(H₂) x P_total

 

The total pressure is given (2.65 atm), so to find the partial pressure of hydrogen, we need to calculate its mole fraction first and then use it in the equation above:

                                                  

\[{\rm{\chi }}\left( {{{\rm{H}}_{\rm{2}}}} \right)\; = \;\frac{{{\rm{n(}}{{\rm{H}}_{\rm{2}}}{\rm{)}}}}{{{\rm{n(}}{{\rm{H}}_{\rm{2}}}{\rm{)}}\; + \;{\rm{n(C}}{{\rm{H}}_{\rm{4}}}{\rm{)}}\; + \;{\rm{n(}}{{\rm{N}}_{\rm{2}}}{\rm{)}}}}\]

 

\[{\rm{\chi }}\left( {{{\rm{H}}_{\rm{2}}}} \right)\; = \;\frac{{{\rm{0}}{\rm{.730}}}}{{{\rm{0}}{\rm{.730}}\; + \;0.456\; + \;{\rm{0}}{\rm{.540}}}}\; = \;0.423\]

 

P(H₂) = 0.423 x 2.65 atm = 1.12 atm

 

Let’s do another example where the mole fraction of a gas needs to be determined.

The partial pressures of CH₄, C₃H₈, and C₄H₁₀ in a gas mixture are 270 torr, 1016 torr, and 1142 torr, respectively. What is the mole fraction of butane (C₄H₁₀)?

In this case, we need to rearrange the formula correlating the partial pressure of butane and the total pressure:

 

P(C₄H₁₀) = χ(C₄H₁₀) x P_total

 

\[{\rm{\chi }}\left( {{{\rm{C}}_{\rm{4}}}{{\rm{H}}_{{\rm{10}}}}} \right)\;{\rm{ = }}\;\frac{{{\rm{P}}\left( {{{\rm{C}}_{\rm{4}}}{{\rm{H}}_{{\rm{10}}}}} \right)}}{{{{\rm{P}}_{{\rm{total}}}}}}\]

 

\[{\rm{\chi }}\left( {{{\rm{C}}_{\rm{4}}}{{\rm{H}}_{{\rm{10}}}}} \right)\;{\rm{ = }}\;\frac{{{\rm{1142}}}}{{{\rm{270}}\;{\rm{ + }}\;{\rm{1016}}\;{\rm{ + }}\;{\rm{1142}}}}\; = \;0.470\]

 

Check Also

• Ideal-Gas Laws
• Combined Gas Law Equation
• How to Know Which Gas Law Equation to Use
• Molar Mass and Density of Gases
• Graham’s Law of Effusion and Diffusion
• Dalton’s Law of Partial Pressures
• Gases in Chemical Reactions
• Gases – Practice Problems