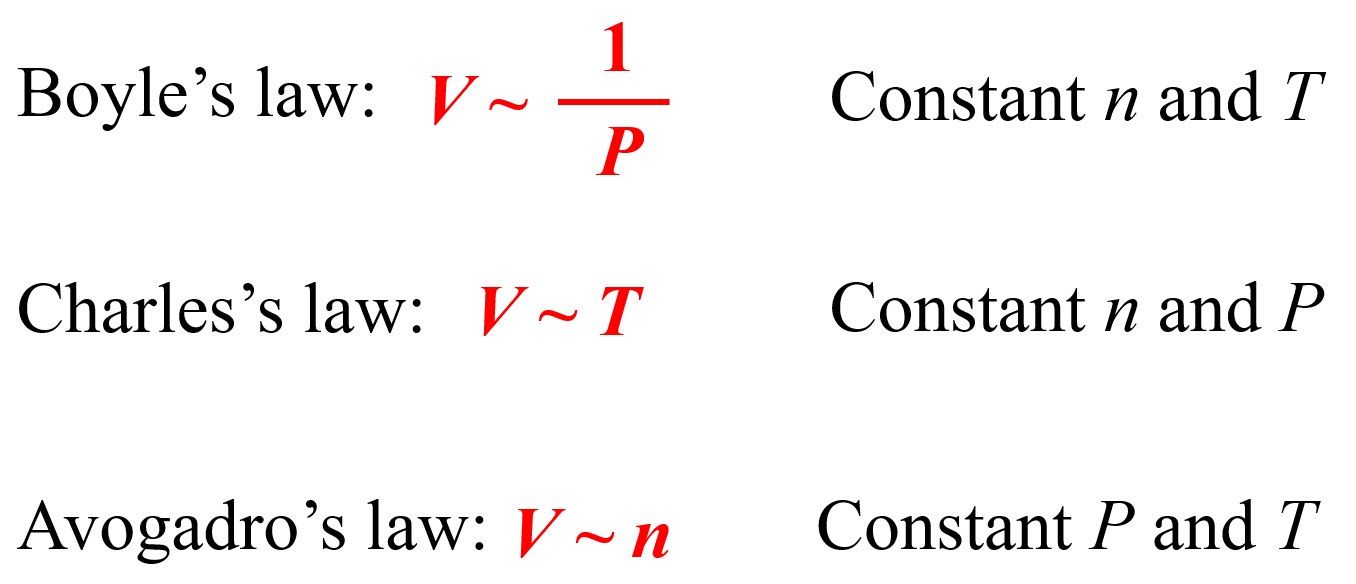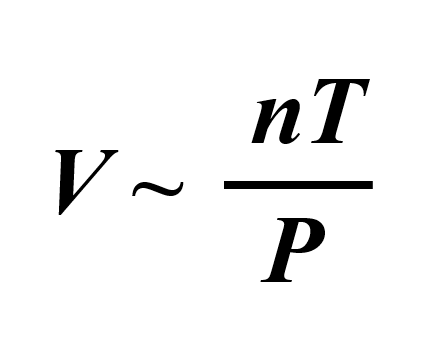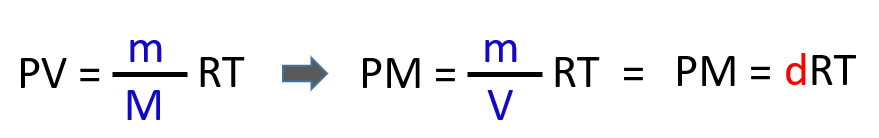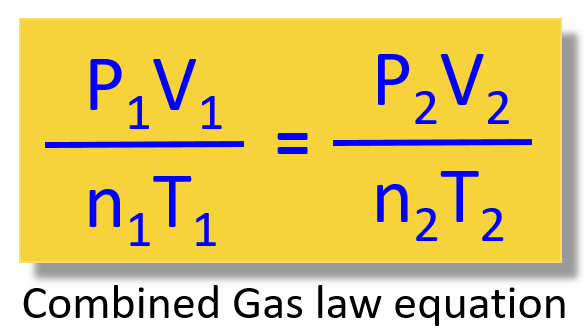The ideal gas laws show the correlation of the temperature, pressure, volume, and the amount of a gas. It is derived from the individual gas laws such as the Boyle’s law, Charles’ law, etc. Remember, when discussing those, we used a pump with a freely moving plunger and by changing the parameters one by one, we were able to get the following correlations:
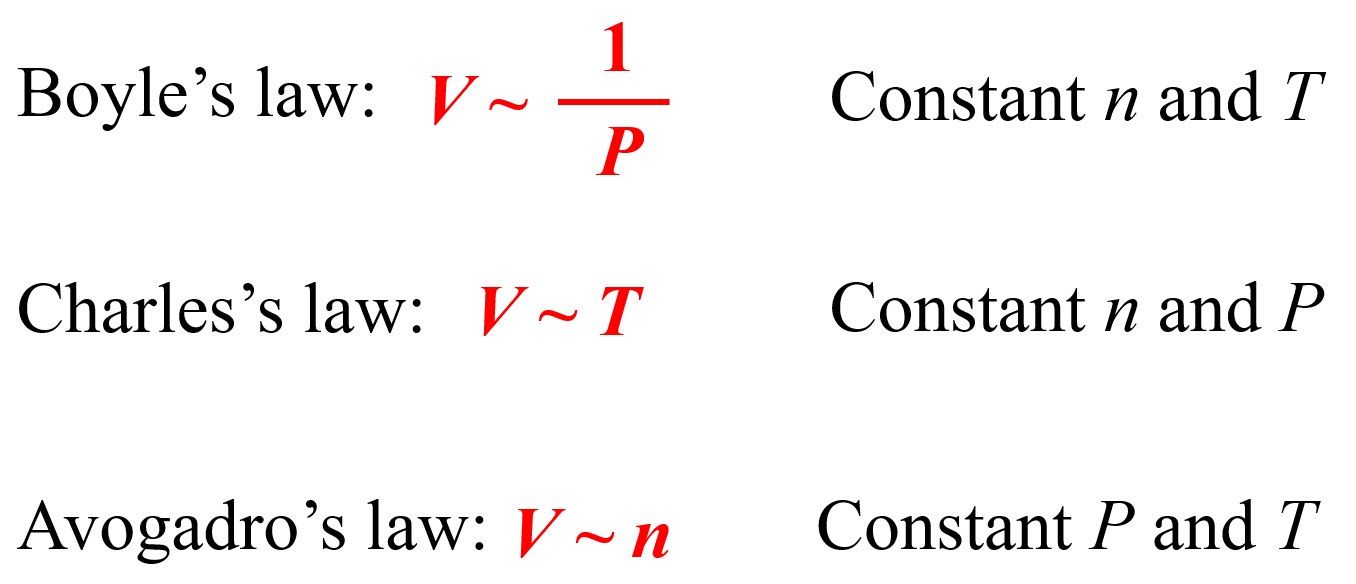
We can combine all of these to get an expression showing how, for example, the volume of an ideal gas is correlated to the temperature, pressure, and the moles of the gas:
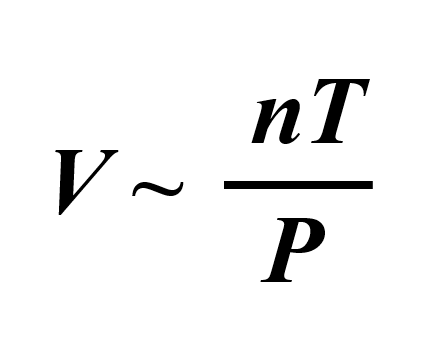
To bring in the equal sign, we introduce a constant:
This can be explained using the example of a car dealership income. The income depends on the number of sales which we can represent as:
income ~ number of cars sold
However, we cannot say income = number of cars sold, so to switch an equal sign, we need to introduce a constant. This can be the price of the car transforming the equation to:
Income = price x number of cars
Now, for the parameters of ideal gases, the constant is the R, which is called the ideal gas constant.
\[V\;{\rm{ = }}\,R\, \times \,\frac{{nT}}{P}\]
By rearranging it, we obtain the ideal gas law equation:
Again, R is called the ideal gas constant. Although it has different values and units, you will mostly be using this:
\[R\;{\rm{ = }}\;{\rm{0}}{\rm{.08206}}\;\frac{{{\rm{L}} \cdot {\rm{atm}}}}{{{\rm{mol}} \cdot {\rm{K}}}}\]
The Ideal Gas Law in Problems
The ideal gas law equation is used when you need to find P, V, T, or n, for the system where they do not change.
For example, A sample of hydrogen gas is added into a 5.80 L container at 56.0 °C. How many moles of the gas are present in the container if the pressure is 6.70 atm?
Rearrange the ideal gas law to get an expression for the moles (n):
PV = nRT
\[{\rm{n}}\;{\rm{ = }}\;\frac{{{\rm{PV}}}}{{{\rm{RT}}}}\]
Now, before entering the numbers, remember to always convert the temperature to Kelvin whenever solving a gas problem:
T = 56.0 oC + 273 = 329 K
And now, we can plug in the numbers:
\[{\rm{n}}\;{\rm{ = }}\;\frac{{{\rm{6}}{\rm{.70}}\;\cancel{{{\rm{atm}}}}\; \times \;{\rm{5}}{\rm{.80}}\;\cancel{{\rm{L}}}}}{{{\rm{0}}{\rm{.08206}}\;\cancel{{\rm{L}}}\;\cancel{{{\rm{atm}}}}\;\cancel{{{{\rm{K}}^{{\rm{ – 1}}}}}}\;{\rm{mo}}{{\rm{l}}^{{\rm{ – 1}}}}{\rm{ }} \times \;{\rm{329}}\;\cancel{{\rm{K}}}}}\; = \;1.44\;{\rm{mol}}\]
Molar Mass and Density of Gases
Density and molar mass are calculated by modifying the ideal gas law equation. What we do is first replace the moles (n) in PV = nRT with mass over the molar mass:
n(moles)=m(mass)M(molarmass)n(moles)=m(mass)M(molarmass)
Next, we rearrange this formula to bring the V under the m which is the density of the gas (mass/volume = density):
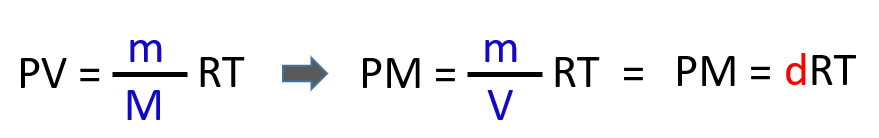
From this equation, we can obtain an expression for the density and molar mass of an ideal gas:
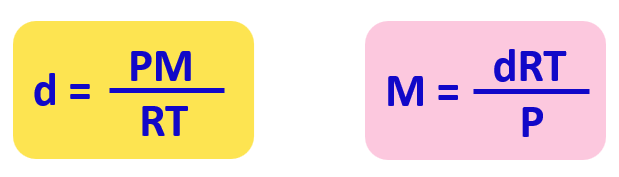
Check this article for details and some examples of determining the molar and the density using the ideal gas law equation.
How do I know which gas law to use?
When the problem has varying parameters, then instead of trying to figure out which gas law to use, you can go with the combined gas law equation:
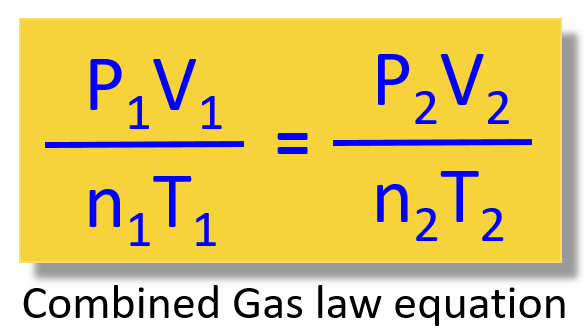
Let’s keep it for another article because there is quite a lot of information in this one.
Here are some summary of gas law problems and if you are not sure how to start, make sure to check the articles on the gas law chapter.
2.
After changing the pressure of a gas sample from 760.0 torr to 0.800 atm, it occupies 4.30 L volume. What was the initial volume of the gas?
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
4.
The volume of a gas decreased from 2.40 L to 830. mL and the final temperature is set at 40.0 °C. Assuming a constant pressure, calculate the initial temperature of the gas in kelvins.
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
6.
A sample of hydrogen gas is added in a 5.80 L container at 56.0 °C. How many moles of the gas are present in the container if the pressure is 6.70 atm?
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
8.
A 3.7 L gas sample, initially at STP, is heated to 280. °C at constant volume. Calculate the final pressure of the gas in atm.
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
9.
A 2.65 g sample of dry ice (solid carbon dioxide) is placed in a 2.90-L vessel and converted into CO2 gas. Calculate the pressure inside the vessel if the temperature is at 35.0 oC.
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
10.
A gas sample is stored in a 429 mL container at 9.50°C and 2.20 atm. Calculate the pressure of the gas if the volume changes to 134 mL and the container is heated to 134.5°C? Assume a constant amount of gas.
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
11.
A gas sample occupies 22.0 L at 171°C and 1.43 atm. Calculate the volume of the gas if its temperature and pressure are increased to 197 °C and 1.80 atm respectively.
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
12.
A sample of ethylene gas (C2H6) collected in a 36.4 mL vessel with a freely moving piston, at 31.0 °C exerts 745 mmHg pressure. What is the volume of this gas at STP?
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
13.
A gas-filled balloon having a volume of 3.50 L at 1.30 atm and 25.0 °C is allowed to rise 5 km above the surface of Earth, where the temperature and pressure are 12.0 °C and 1.10 atm, respectively. What would the volume of the balloon be in these conditions?
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
15.
Determine the density of ammonia gas, NH3, at 36.0 oC and 695 mmHg. Report the density in grams per liter.
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
16.
A scientist carries out an experiment to determine the molar mass of a 2.84-g sample of a colorless liquid which exerts 756 mmHg pressure when vaporized in a 260-mL flask at 142 oC. What is the molecular mass of this compound?
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
17.
Identify the unknown gas that weighs 17.75 grams in a 17.0 L cylinder held at 0.700 atm pressure and 250°C.
a) NO2 b) CO2 c) H2 d) SO2 e) He
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
19.
The rate of effusion of an unknown gas is 9.20 mL/min. Under identical conditions, the rate of effusion of pure nitrogen (N2) gas is 14.65 mL/min. Identify the unknown gas using the Graham’s law.
a) O2 b) C3H8 c) C4H10 d) NO2 e) Cl2
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
video
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
20.
A sample of krypton effuses from a container in 95 seconds. The same amount of an unknown gas requires 55 seconds. Identify the unknown gas.
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
21.
If a sample of Br2 vapor can effuse from an opening in a heated vessel in 46 s, how long will it take the same amount of He to effuse under identical conditions?
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
22.
It has been demonstrated that 3.56 mL of an unknown gas effuses through a hole in the same time that 8.64 mL of argon does under the same conditions. Determine the molecular mass of the unknown gas.
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
23.
What is the partial pressure of nitrogen in a mixture of N2, SO2 and CO2 that has a total pressure of 6.84 atm. The partial pressure of SO2 is 2.10 atm, and the partial pressure of CO2 is 1.74 atm.
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
24.
13.2 grams of CO2 and 6.00 grams of He are mixed in a 4.00 L container at 300. K. Calculate the partial pressure of both gases and the total pressure of the mixture.
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
25.
A 3.00-L bulb containing N2 at 1.80 atm pressure is connected to a 2.00-L bulb filled with H2 at 3.50 atm pressure. What is the final pressure of the system when the valve is opened?
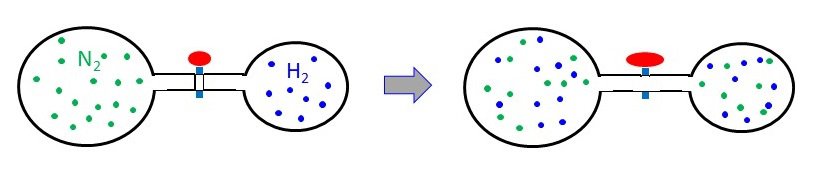
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
video
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
26.
Assuming ideal gas behavior, calculate the total pressure (in atm) of a mixture of 0.0260 mol of nitrogen, N2, and 0.0170 mol of argon, Ar, in a 3.50-L flask at 20 oC.
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
27.
A mixture of gases contains CH4, N2, and H2 and exerts a total pressure of 2.65 atm. The mixture contains 0.456 mol of CH4, 0.540 mol of N2 and 0.730 mol of H2. What is the partial pressure of hydrogen in atmospheres?
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
28.
The partial pressures of CH4, C3H8, and C4H10 in a gas mixture are 270 torr, 1016 torr, and 1142 torr, respectively. What is the mole fraction of butane (C4H10)?
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
29.
In a mixture of two gases, the partial pressure of CO2(g) is 0.145 atm and that of O2(g) is 0.370 atm.
a) What is the mole fraction of each gas in the mixture?
b) Calculate the total number of moles of gas in the mixture if the mixture occupies a volume of 12.5 L at 45.0 °C.
c) Calculate the number of grams of each gas in the mixture.
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
30.
Oxygen can be prepared in the laboratory by decomposing potassium chlorate, KClO3 according to the following reaction:
2KClO3(s) → 2KCl(s) + 3O2(g).
How many liters of oxygen can be produced from 4.80 g KClO3, if the reaction is carried out at standard conditions?
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
video
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
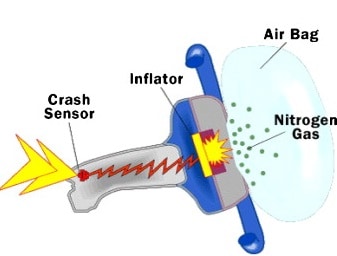
31.
Sodium azide is used in automobile airbags as a source of nitrogen gas to rapidly inflate the bags upon a hit. If the volume of the airbag is 7.95 L, what mass of NaN3 is required to produce enough nitrogen to fill it at 23.0 °C and 1.20 atm?
2NaN3(s) → 2Na(s) + 3N2(g)
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
video
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
32.
Calcium hydride (CaH2) can be used as a drying agent and a source of Hydrogen, because of its high reactivity with water.
CaH2(s) + 2 H2O(l) → Ca(OH)2(aq) + 2H2(g)
How many grams of CaH2 are needed to produce 76.8 L of H2 gas at a pressure of 0.750 atm and a temperature of 25 °C?
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
33.
Propane (C3H8) is used as a fuel in gas barbecue grills. How many liters of oxygen, taken at STP, are needed for the full combusting of 26.4 g of propane?
C3H8(g) + 5O2(g) → 3CO2(g) + 4H2O(l)
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
34.
Lithium hydroxide (LiOH) is used in space shuttles to absorb the carbon dioxide exhaled by astronauts according to the following equation:
2LiOH(s) + CO2(g) → Li2CO3(s) + H2O(l)
How many liters of carbon dioxide gas at 23.0 oC and 732 mmHg could be absorbed by 284 g of lithium hydroxide?
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
35.
In a particular reaction, at 25 °C, 16.4 L of carbon monoxide at a 950.0 torr is mixed with 11.2 g of iron (III) oxide, and 5.68 g iron is obtained. What is the percent yield of the reaction?
Fe2O3 + 3CO(g) → 2Fe + 3CO2(g)
answer
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
Solution
This content is available to registered users only.
Click here to Register!
By joining Chemistry Steps, you will gain instant access to the answers and solutions for all the Practice Problems and the powerful set of General Chemistry 1 and 2 Summary Study Guides.
