The combined gas law is obtained by rearranging the ideal gas law, from PV = nRT.
From this, we obtain an expression for the R:
\[{\rm{R}}\; = \;\frac{{{\rm{PV}}}}{{{\rm{nT}}}}\]
Now, because R is constant, this expression is true for any parameters of P, V, n, and T. Therefore, we can write that:
\[\frac{{{{\rm{P}}_{\rm{1}}}{{\rm{V}}_{\rm{1}}}}}{{{{\rm{n}}_{\rm{1}}}{{\rm{T}}_{\rm{1}}}}}\; = \;\frac{{{{\rm{P}}_{\rm{2}}}{{\rm{V}}_{\rm{2}}}}}{{{{\rm{n}}_{\rm{2}}}{{\rm{T}}_{\rm{2}}}}}\]
So, remember, this is the combined gas law equation and the great thing about it is that it allows you not to memorize all the other gas laws and decide every time which one to use when solving a problem:

For example,
What will be the final volume of a 3.50 L sample of nitrogen at 20.0 °C if it is heated to 200. °C?
First, write down what is given and what needs to be determined:
V1 = 3.50 L
T1 = 20 oC
T2 = 200. oC
V2 = ?
Second, remember to always convert the temperature to Kelvin in any gas problem:

So, T1 = 20 + 273 = 293 K, T2 = 200 + 273 = 473 K
We solved this problem last time when talking about the ideal gas laws, however, there we needed to remember or figure out that it is based on Charle’s law.
Suppose we don’t know which law to use. For this what you do is:
Write the combined gas law equation and cancel the constants. In this case, n and P because there is nothing mentioned about them.
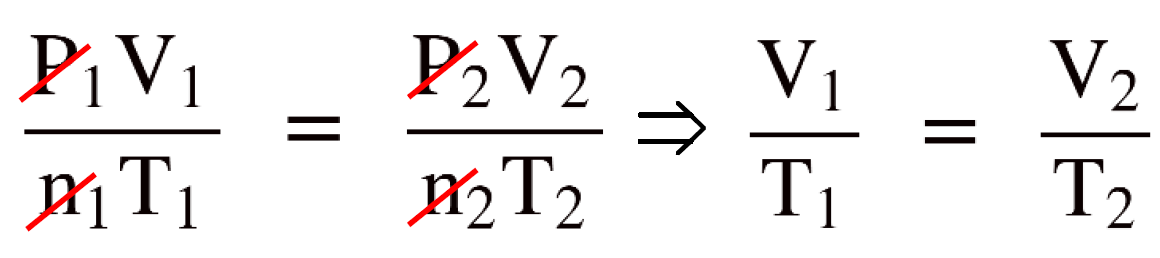
By canceling the constants in the combined gas law, we now have the Charle’s law and to determine V2 , we just need to rearrange the equation and plug the numbers:
\[\frac{{{{\rm{V}}_{\rm{1}}}}}{{{{\rm{T}}_{\rm{1}}}}}\; = \;\frac{{{{\rm{V}}_{\rm{2}}}}}{{{{\rm{T}}_{\rm{2}}}}}\]
\[{{\rm{V}}_{\rm{2}}}\; = \;\frac{{{\rm{473}}\;\cancel{{\rm{K}}}\;{\rm{ \times }}\;{\rm{3}}{\rm{.50}}\;{\rm{L}}}}{{{\rm{293}}\;\cancel{{\rm{K}}}}}\;{\rm{ = }}\;{\rm{5}}{\rm{.65}}\;{\rm{L}}\]
This strategy can be used to solve any gas problem when the P, V, N, and T parameters are changing. If it is a stationary system and you are asked to determine the n, P, V, or T , then you need to use the ideal gas law equation: PV = nRT
Let’s do one more example using the combined gas law equation when three parameters are being changed.
A gas sample is stored in a 429 mL container at 9.50°C and 2.20 atm. Calculate the pressure of the gas if the volume changes to 134 mL and the container is heated to 134.5°C? Assume a constant amount of gas.
First assign the states and write down what is given and what needs to be determined:
P1 = 2.20 atm
T1 = 9.50°C
V1 = 429 mL
T2 = 134.5°C
V2 = 134 mL
P2 = ?
Next, write the combined gas law equation, and remove the moles (n) because there is nothing mentioned about them, and we assume that they do not change:
\[\frac{{{{\rm{P}}_{\rm{1}}}{{\rm{V}}_{\rm{1}}}}}{{{{\rm{T}}_{\rm{1}}}}}\; = \;\frac{{{{\rm{P}}_{\rm{2}}}{{\rm{V}}_{\rm{2}}}}}{{{{\rm{T}}_{\rm{2}}}}}\]
\[{{\rm{P}}_{\rm{2}}}\; = \;\frac{{{{\rm{P}}_{\rm{1}}}{{\rm{V}}_{\rm{1}}}{{\rm{T}}_{\rm{2}}}}}{{{{\rm{T}}_{\rm{1}}}{{\rm{V}}_{\rm{2}}}}}\]
Make sure the temperature are in Kelvin:
T1 = 9.50 + 273 = 282.5 K
T2 = 134.5° + 273 = 407.5 K
Finally, enter the numbers to determine P2:
\[{{\rm{P}}_{\rm{2}}}\; = \;\frac{{{{\rm{P}}_{\rm{1}}}{{\rm{V}}_{\rm{1}}}{{\rm{T}}_{\rm{2}}}}}{{{{\rm{T}}_{\rm{1}}}{{\rm{V}}_{\rm{2}}}}}\; = \;\frac{{{\rm{2}}{\rm{.20}}\;{\rm{atm}}\;{\rm{ \times }}\;{\rm{429}}\;\cancel{{{\rm{mL}}}}\;{\rm{ \times }}\;{\rm{407}}{\rm{.5}}\;\cancel{{\rm{K}}}}}{{{\rm{282}}{\rm{.5}}\;\cancel{{{\rm{K}}\;}}\;{\rm{134}}\;\cancel{{{\rm{mL}}}}}}\;{\rm{ = }}\;{\rm{10}}{\rm{.2}}\;{\rm{atm}}\]
Check Also
- Ideal-Gas Laws
- How to Know Which Gas Law Equation to Use
- Molar Mass and Density of Gases
- Graham’s Law of Effusion and Diffusion
- Dalton’s Law of Partial Pressures
- Mole Fraction and Partial Pressure of the Gas
- Gases in Chemical Reactions
- Gases – Practice Problems
Practice
A gas sample is stored in a 429 mL container at 9.50°C and 2.20 atm. Calculate the pressure of the gas if the volume changes to 134 mL and the container heated to 134.5°C? Assume a constant amount of gas.
A gas sample occupies 22.0 L at 171°C and 1.43 atm. Calculate the volume of the gas if its temperature and pressure are increased to 197°C and 1.80 atm respectively.
