Density and molar mass are calculated by modifying the ideal gas law equation. What we do is first replace the moles (n) in PV = nRT with mass over the molar mass:
\[{\rm{n}}\;{\rm{(moles)}}\,{\rm{ = }}\;\frac{{{\rm{m}}\;{\rm{(mass)}}}}{{{\rm{M}}\;{\rm{(molar}}\,{\rm{mass)}}}}\]

Next, we rearrange this formula to bring the V under the m which is the density of the gas (mass/volume = density):
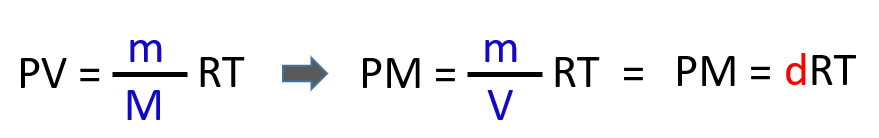
From this equation, we can obtain an expression for the density and molar mass of an ideal gas:
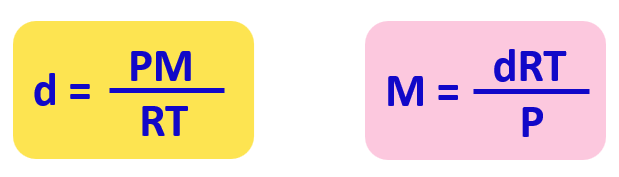
An example of calculating the density of an ideal gas:
What is the density of CO2 gas at 386 K and 17.0 atm.
\[{\rm{d}}\;{\rm{ = }}\;\frac{{{\rm{PM}}}}{{{\rm{RT}}}}\]
\[{\rm{d}}\;{\rm{ = }}\;\frac{{{\rm{17}}{\rm{.0}}\;\cancel{{{\rm{atm}}}}\;{\rm{44}}{\rm{.0}}\;{\rm{g}}\;\cancel{{{\rm{mo}}{{\rm{l}}^{{\rm{ – 1}}}}}}}}{{{\rm{0}}{\rm{.08206}}\;{\rm{L}}\;\cancel{{{\rm{atm}}}}\;\cancel{{{{\rm{K}}^{{\rm{ – 1}}}}}}\;\cancel{{{\rm{mo}}{{\rm{l}}^{{\rm{ – 1}}}}}}{\rm{ 386}}\;\cancel{{\rm{K}}}}}\;{\rm{ = }}\;{\rm{23}}{\rm{.6}}\;{\rm{g/L}}\]
An example of calculating the molar mass of an ideal gas:
A scientist carries out an experiment to determine the molar mass of a 2.84-g sample of a colorless liquid which exerts 756 mmHg pressure when vaporized in a 260-mL flask at 142 oC. What is the molecular mass of this compound?
\[{\rm{PV}}\;{\rm{ = }}\;{\rm{nRT}}\]
\[{\rm{PV}}\;{\rm{ = }}\;\frac{{\rm{m}}}{{\rm{M}}}{\rm{RT}}\]
\[{\rm{M}}\;{\rm{ = }}\;\frac{{{\rm{mRT}}}}{{{\rm{PV}}}}\]
\[{\rm{M}}\;{\rm{ = }}\;\frac{{{\rm{2}}{\rm{.84}}\;{\rm{g }}\;{\rm{0}}{\rm{.08206}}\;\cancel{{\rm{L}}}\;\cancel{{{\rm{atm}}}}\;\cancel{{{{\rm{K}}^{{\rm{ – 1}}}}}}\;{\rm{mo}}{{\rm{l}}^{{\rm{ – 1}}}}\;{\rm{415}}\;\cancel{{\rm{K}}}}}{{{\rm{0}}{\rm{.995}}\;\cancel{{{\rm{atm}}}}\;{\rm{0}}{\rm{.260}}\;\cancel{{\rm{L}}}}}\;{\rm{ = }}\;{\rm{374}}\;{\rm{g/mol}}\]
Check Also
- Ideal-Gas Laws
- Combined Gas Law Equation
- How to Know Which Gas Law Equation to Use
- Graham’s Law of Effusion and Diffusion
- Dalton’s Law of Partial Pressures
- Mole Fraction and Partial Pressure of the Gas
- Gases in Chemical Reactions
- Gases – Practice Problems
Practice
Identify the unknown gas that weighs 17.75 grams in a 17.0 L cylinder held at 0.700 atm pressure and 250°C.
a) NO2 b) CO2 c) H2 d) SO2 e) He
What is the density of CO2 gas at 386 K and 17.0 atm.
Determine the density of ammonia gas, NH3, at 36.0 oC and 695 mmHg. Report the density in grams per liter.
A scientist carries out an experiment to determine the molar mass of a 2.84-g sample of a colorless liquid which exerts 756 mmHg pressure when vaporized in a 260-mL flask at 142 oC. What is the molecular mass of this compound?
